Как записать габариты цилиндра

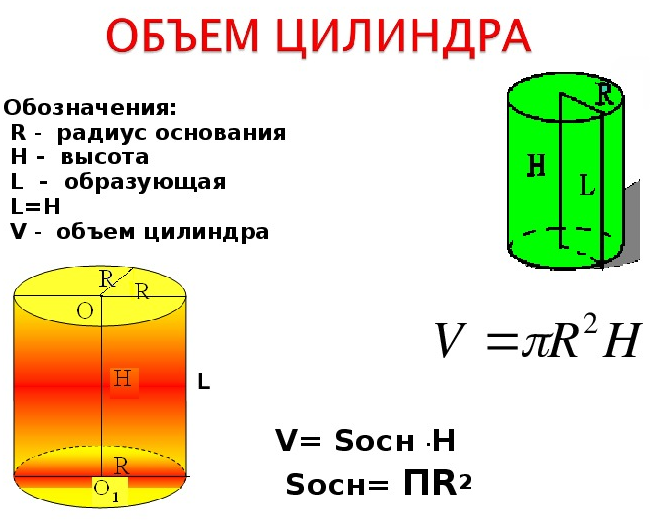
Объем цилиндра, формулы и калькулятор для вычисления объема цилиндра и площади его поверхностей, а также необходимая теория о характеристиках цилиндра.

Видео:11 класс. Геометрия. Объем цилиндра. 14.04.2020Скачать

Объем правильного цилиндра через радиус и высоту цилиндра

Видео:Цилиндр - расчёт площади, объёма.Скачать

Формулы и калькулятор для вычисления объема цилиндра через площадь основания и высоту цилиндра

Видео:Объём цилиндраСкачать

Формулы и калькулятор для вычисления объема цилиндра через диаметр основания

Видео:Объем цилиндра.Скачать

Объем цилиндрической полости

Объем полости в виде цилиндра равен объему цилиндра, который извлечен из данной полости для ее образования. То есть для вычисления цилиндрической полости можно воспользоваться формулами и калькулятором для расчета простого правильного цилиндра в зависимости от известных исходных данных.

На картинке продемонстрирована цилиндрическая полость, образованная в теле путем извлечения из него цилиндра. Объем извлеченного цилиндра и объем образованной полости равны.

Нужно отметить один важный момент. Несмотря на равенство объемов извлеченного цилиндра и образованной полости, площади поверхностей данных объектов будут отличаться, так как у образованной цилиндрической полости отсутствует верхняя поверхность. То есть суммарная площадь поверхности образованной цилиндрической полости будет меньше суммарной площади извлеченного цилиндра на одну площадь основания цилиндра.

Правильный цилиндр – это цилиндр, где угол между образующими боковой поверхности и основанием цилиндра равен 90 градусов.

Неправильный или наклонный цилиндр – это цилиндр, где угол между образующими боковой поверхности и основанием цилиндра отличается от 90 градусов.

Рассмотрим правильный цилиндр.

Цилиндр – это тело, образованное вращением прямоугольника вокруг одной из его сторон. Тело цилиндра ограничено двумя кругами, называемыми основанием цилиндра и боковой цилиндрической поверхностью, которая в развертке представляет собой прямоугольник

Цилиндр можно так же описать как тело, состоящее из двух равных кругов, не лежащих в одной плоскости и параллельных между собой, и отрезков, соединяющих все точки одной окружности, с соответствующими точками другой окружности. Данные отрезки называются образующими цилиндра.

Радиус основания цилиндра, является радиусом цилиндра.

Ось цилиндра – это прямая, соединяющая центра оснований цилиндра.

Высота цилиндра – это перпендикуляр, опущенный от одного основания цилиндра к другому.

Видео:Объем цилиндраСкачать

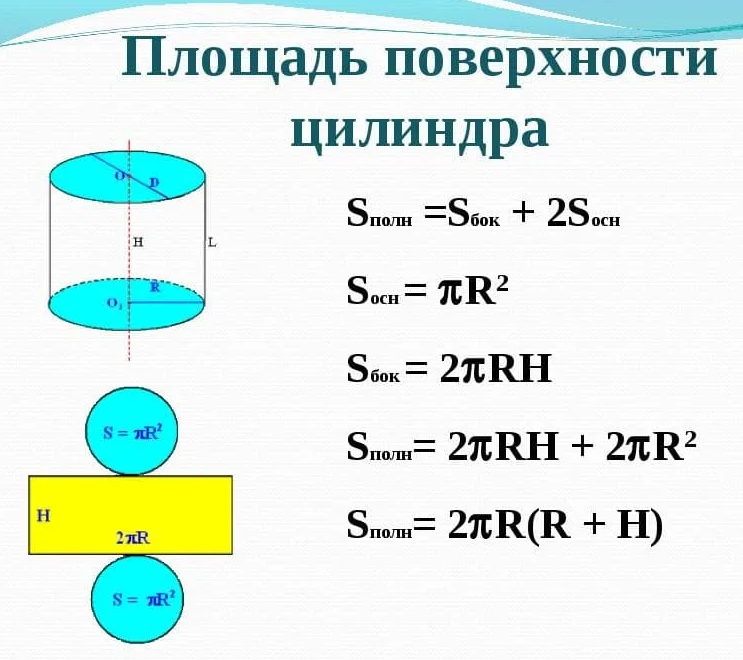
Поверхности цилиндра

Наружную поверхность цилиндра можно условно разделить на три отдельные поверхности: верхняя, нижняя и боковая.

Верхняя и нижняя поверхности цилиндра имеют форму круга и равны между собой.

Боковая поверхность цилиндра имеет форму прямоугольника. Чтобы это наглядно представить, возьмем боковую наружную поверхность цилиндра и мысленно сделаем вертикальный разрез по образующей цилиндра. Далее развернем поверхность на плоскость. В результате увидим, что боковая поверхность имеет форму прямоугольника (см. на картинке).

Читайте также: Замена главного цилиндра сцепления газон некст двигатель ямз

Видео:11 класс, 32 урок, Объем цилиндраСкачать

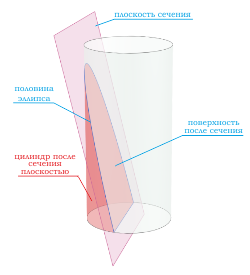
Сечения цилиндра

При сечении цилиндра плоскостью, проходящей через оба основания цилиндра под углом в 90 градусов, всегда получатся прямоугольная фигура .

При сечении цилиндра плоскостью, проходящей через оба основания цилиндра под углом отличным от 90 градусов, получатся фигура, похожая на прямоугольник , но две боковые стороны которого будут являться кривыми линиями.

Если секущая поверхность проходит параллельно основаниям цилиндра, то сечением будет круг .

Если секущая поверхность проходит через боковую поверхность, но при этом не параллельна основанию цилиндра, то в сечении получается эллипс .

Если секущая поверхность проходит через одно основание цилиндра и боковую поверхность, то в сечение будет фигура в виде половины эллипса .

Видео:11 класс. Геометрия. Объем цилиндраСкачать

Что такое объем

Объем тела (геометрической фигуры) – это количественная характеристика, характеризующая количество пространства, занимаемого телом. Объем выражается в кубических единицах измерения, например: мм 3 , см 3 , мл 3 .

Формула вычисления объема цилиндра часто применяются при расчете массы различных цилиндров, например, прутков, заготовок и т.п. Для вычисления массы, необходимо вычисленный объем цилиндра умножить на плотность материала из которого цилиндр.

Так же, вычислить объём цилиндра иногда требуется для определения полости в виде цилиндра (цилиндрическая полость). В данном случае объём полости будет равен объёму цилиндра, который полностью занимает эту полость.

Объем и площадь других видов цилиндров рассмотрен в статьях:

Видео:Видеоурок по математике "Цилиндр"Скачать

Геометрические тела. Цилиндр.

Цилиндр − это геометрическое тело, которое ограничено цилиндрической поверхностью и 2-мя плоскостями, которые параллельны и пересекают ее.

ABCDEFG и abcdefg — это основания цилиндра. Расстояние между основаниями (KM) – высота цилиндра.

Цилиндрические сечения боковой поверхности кругового цилиндра.

Сечения, которые идут параллельно к основанию, будут являться кругами одного радиуса. Сечения, которые параллельны образующим цилиндра — это пары параллельных прямых (AB || CD). Сечения, не параллельные ни основанию, ни образующим, являются эллипсами.

Цилиндрическая поверхность образуется посредством движения прямой параллельно самой себе. Точка прямой, которая выделена, перемещается вдоль заданной плоской кривой – направляющей. Эта прямая называется образующей цилиндрической поверхности.

Прямой цилиндр – это такой цилиндр, в котором образующие перпендикулярны основанию. Если образующие цилиндра не перпендикулярны основанию, то это будет наклонный цилиндр.

Круговой цилиндр – цилиндр, основанием которого является круг.

Круглый цилиндр – такой цилиндр, который одновременно и прямой, и круговой.

Прямой круговой цилиндр определяется радиусом основания R и образующей L, которая равна высоте цилиндра H.

Призма – это частный случай цилиндра.

Видео:Объём цилиндра измерили с помощью мензурки (см. рисунок). Масса цилиндра равна 320 г. - №27231Скачать

Формулы нахождения элементов цилиндра.

Площадь боковой поверхности прямого кругового цилиндра:

Площадь полной поверхности прямого кругового цилиндра:

Объем прямого кругового цилиндра:

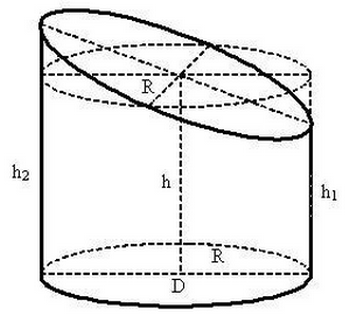
Прямой круговой цилиндр со скошенным основанием либо кратко скошенный цилиндр определяют с помощью радиуса основания R, минимальной высоты h₁ и максимальной высоты h₂.

Площадь боковой поверхности скошенного цилиндра:

Площадь оснований скошенного цилиндра:

Площадь полной поверхности скошенного цилиндра:

Объем скошенного цилиндра:

S_бок — площадь боковой поверхности;

Видео:КАК ИЗМЕРИТЬ ЦИЛИНДРЫ? Учимся пользоваться нутромером и микрометромСкачать

Как рассчитать, вычислить объём цилиндра? Что нужно для этого?

Цилиндром называется геометрическое тело, образованное путем вращения прямоугольника вокруг его стороны (преимущественно большей). Круги, лежащие в основании, конгруэнтные – соразмерные, равные.

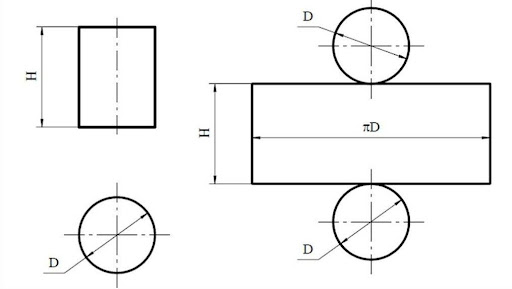
Поверхность тела имеет криволинейную форму – цилиндрическую. Рассмотрим, как рассчитать объем цилиндра: полного и усеченного при наличии разных исходных данных. Развертка геометрического тела представлена:

• прямоугольником с шириной, равной высоте геометрического тела (H);
• длиной, равной образующей или радиусу нижней поверхности: c = πD = 2πr.

Видео:Объём цилиндраСкачать

Объем цилиндра

Объемом называется характеристика ограниченного геометрическим телом пространства. Показывает, сколько места занимает тело или сколько жидкости внутрь него можно залить. Близкие по значению слова – емкость, вместимость.

Существует несколько формул, позволяющих найти объем цилиндра; какая подойдет, зависит от исходной информации.

• π – число «Пи», равное приблизительно 3,1415;
• r – радиус круга;
• h – высота призмы или длина стороны прямоугольника, вокруг которой он вращался для образования цилиндра.

V=\pi \frac или \frac \pi d^2h, где:

• d – диаметр геометрического тела.

Рассмотрим, как вычислить объем цилиндра на практике, если известны его:

• радиус: r = 5 см;
• высота: h = 13 см.

Подставляем значения в формулу:

V = π * 5 2 * 13 = π * 25 * 13 = 325 π.

Если нужно реальное число, вместо π в формулу подставим его округленное значение 3,1415.

V = 325 * 3,1415 ≈ 1020,98 ≈ 1021 см 3 .

В случае, когда дан диаметр круга, его придется разделить на два для получения радиуса: r= \frac d или разделить на четыре после поднесения к квадрату; r= (\frac d) =\frac d^2.

Видео:Объем цилиндра. Практическая часть. 11 класс.Скачать

Формула для вычисления объема усеченного цилиндра

Усеченным называется цилиндр, часть которого отрезана плоскостью, пролегающей не параллельно нижней плоскости.

Формула объема усеченного цилиндра следующая:

здесь h₁ b h₂ – наименьшая и наибольшая высоты геометрического тела.

После подстановки значений получится выражение:

Первый: воспользуемся формулой V= \pi r^2 *\frac . Для этого определим радиус нижней плоскости.

r = \frac d= \frac 10=5 см.
V=\pi r^2 *\frac = \pi *5^2* \frac = 25 \pi * 20 = 500 \pi \approx 1570,75 см 3 .

Второе решение – подставим диаметр в формулу:

V = \pi \frac * \frac = \pi *\frac * \frac = \pi * \frac * \frac = 500 \pi \approx 1570,75 см 3 .

Зная высоту и радиус или диаметр основания тела, его вместительность высчитывается в несколько действий.

Видео:Объем цилиндра.Скачать

Как найти высоту цилиндра, с помощью данных?

Видео:ЕГЭ-2020: Изменение объёма цилиндраСкачать

Объем цилиндра формула (через радиус основания и высоту)

r — радиус основания цилиндра,

Если внимательно посмотреть на эту формулу, то можно заметить, что

— это формула площади круга, а в нашем случае — площадь основания. Поэтому формулу объема цилиндра можно записать через площадь основания и высоту:

Видео:Микрометр и нутромер. Как измерить цилиндры?Скачать

S (б.п.) = hP = 2πrh

— Если известна площадь бок. поверхности S (б.п.) и высота h цилиндра, радиус будет равен частному от деления S (б.п.) на произведение 2пи на высоту:

Видео:Поршни одинаковые, а объемы разные на мопеде Альфа.Скачать

Формула вычисления объема цилиндра

1. Через площадь основания и высоту

Объем (V) цилиндра равняется произведению его высоты и площади основания.

2. Через радиус основания и высоту

Как мы знаем, в качестве оснований цилиндра (равны между собой) выступает круг, площадь которого вычисляется так: S = π ⋅ R 2 . Следовательно, формулу для вычисления объема цилиндра можно представить в виде:

V = π ⋅ R 2 ⋅ H

Примечание: в расчетах значение числа π округляется до 3,14.

3. Через диаметр основания и высоту

Как нам известно, диаметр круга равняется двум его радиусам: d = 2R. А значит, вычислить объем цилиндра можно следующим образом:

V = π ⋅ (d/2) 2 ⋅ H

Нет сомнений, что все мы со школьных лет помним, как найти высоту цилиндра, формула выглядит так: H=V/πR^2 или 4V/D^2.

Расшифровать формулу просто:

• V – объем цилиндра;
• π – 3,14;
• R – радиус цилиндра;
• D – диаметр.

То есть получается, что, если разделить объем на площадь основания, получится высота цилиндра.

Можно поступить проще. Для этого нам придется вычислить площадь боковой поверхности искомого цилиндра. Это легко сделать по формуле: S=2πRH. Слегка изменив формулу, получаем: H=S/2πR.

Таким образом, есть уже два способа, которые помогли вспомнить, как найти высоту цилиндра. Это нетрудно, когда перед глазами стройные формулы.

Видео:9 класс, 41 урок, ЦилиндрСкачать

Способ расчета радиуса цилиндра:

Цилиндр – геометрическое тело, которое получается при вращении прямоугольника вокруг его стороны. Также, цилиндр представляет собой тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими ее. Эта поверхность образуется при движении прямой параллельно самой себе. При этом выделенная точка прямой перемещается вдоль определенной плоской кривой (направляющая). Данная прямая называется образующей цилиндрической поверхности.
Формула радиуса цилиндра:
где V – объем цилиндра, h – высота

Цилиндр – геометрическое тело, которое получается при вращении прямоугольника вокруг его стороны. Также, цилиндр представляет собой тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими ее. Эта поверхность образуется при движении прямой параллельно самой себе. При этом выделенная точка прямой перемещается вдоль определенной плоской кривой (направляющая). Данная прямая называется образующей цилиндрической поверхности.
Формула радиуса цилиндра:
где Sb – площадь боковой поверхности, h – высота

Цилиндр – геометрическое тело, которое получается при вращении прямоугольника вокруг его стороны. Также, цилиндр представляет собой тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими ее. Эта поверхность образуется при движении прямой параллельно самой себе. При этом выделенная точка прямой перемещается вдоль определенной плоской кривой (направляющая). Данная прямая называется образующей цилиндрической поверхности.
Формула радиуса цилиндра:
где S – площадь полной поверхности, h – высота

S (п.п.) = S (б.п.) + 2S (осн.) = 2πrh + πr2=πr (2h+r)

Площадь боковой поверхности равняется длине окружности основания умноженной на высоту:

R = √V / πh

где V — объем цилиндра, h — высота.
Полная площадь поверхности цилиндра складывается из сумм площадей его боковой поверхности и двух оснований:

Видео:Как пользоваться микрометромСкачать

Примеры задач

Задание 1
Высота цилиндра равняется 5 см, а объем – 141,3 см 3 . Вычислите его радиус.

Решение:
Воспользуемся соответствующей формулой, подставив в нее известные по условиям задачи значения:

Задание 2
Найдите радиус цилиндра, если площадь его боковой поверхности равна 175,84 см 2 , а высота составляет 7 см.

Решение:
Применим формулу, в которой задействованы заданные величины:

Задание 3
Рассчитайте радиус цилиндра, если полная площадь его поверхности – 602,88 см 2 , а высота – 10 см.

Решение:
Используем третью формулу для нахождения неизвестной величины:

Видео:Отличие цилиндров 110-125сс на мопед alpha, vento и т.п.Скачать

Через площадь боковой поверхности

Радиус цилиндра считается таким образом:

S_бок. – площадь боковой поверхности цилиндра; равна произведению длины окружности (2 π R), являющейся основанием фигуры, на его высоту:

Видео:Задачи на цилиндр. Объем цилиндра - bezbotvyСкачать

Площадь полной поверхности цилиндра через радиус основания и высоту

Формула для нахождения полной поверхности цилиндра через высоту и радиус основания:

, где π — число Пи (3,14159…), r — радиус основания цилиндра, h — высота цилиндра.