В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки А и В, а на окружности другого основания — точки В1 и С1, причем ВВ1 — образующая цилиндра, а отрезок АС1 пересекает ось цилиндра.
а) Докажите, что угол АВС1 прямой.
б) Найдите площадь боковой поверхности цилиндра, если AB = 20, BB1 = 15, B1C1 = 21.
а) Рассмотрим плоскость, проходящую через ось цилиндра и прямую АС1. Обозначим точку пересечения этой плоскости и окружности основания цилиндра, содержащую точку А, через точку С. Тогда СС1 — образующая цилиндра. Отрезок АС пересекает ось цилиндра. Значит, он проходит через центр окружности основания цилиндра, то есть является ее диаметром. Следовательно, угол АВС прямой.
Прямая СС1 является образующей цилиндра, поэтому она перпендикулярна прямой АВ. Таким образом, прямая АВ перпендикулярна плоскости ВСС1б а значит, угол АВС1 прямой.
б) Отрезок AC является диаметром основания цилиндра. Значит, длина
окружности основания цилиндра равна
Следовательно, площадь боковой поверхности цилиндра равна
при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки,
Видео:Видеоурок по математике "Цилиндр"Скачать
Урок геометрии в 11 классе по теме Цилиндр по материалам ЕГЭ
Ищем педагогов в команду «Инфоурок»
Выбранный для просмотра документ Урок геометрии в 11 классе по теме Цилиндр по материалам ЕГЭ.docx
Урок геометрии в 11 классе
по теме «Цилиндр» по материалам ЕГЭ.
Урок составила учитель математики МБОУ СОШ №8 г. Каменск — Шахтинского Ростовской области Семиглазова Нина Ильинична.
научить решать задачи по теме «Цилиндр» по материалам ЕГЭ.
2. Страничка из истории математики.
3. Проверка домашнего задания.
4. Решение задач по готовым чертежам.
7. Домашнее задание по материалам ЕГЭ.
8. Домашнее задание творческого характера.
На экране с помощью проектора появляется первый слайд .
На фоне музыки Клайдермана.
Учитель: Нам надо жить без
Тема нашего урока: «Решение задач по теме «Цилиндр» по материалам ЕГЭ».
А кто из вас знает: кто изобрёл цилиндр?
2.Страничка из истории математики.
Учитель: Открытие цилиндра принадлежит великому Архимеду. На своей могильной плите Архимед повелел выгравировать цилиндр и шар – символы его геометрических открытий. Труды Архимеда в астрономии, геометрии, механике велики и многочисленны.
Вам они известны. Но мне хотелось бы вам рассказать об Архимеде- Человеке, Патриоте своей Родины. И сегодня нельзя без восхищения и удивления читать дошедшие до нас строки Плутарха, рассказывающие об осаде Сиракуз римским полководцем Марцеллом. Десятки сконструированных Архимедом катапульт всех «калибров» метали каменья в корабли захватчиков, на их головы неслись тучи копий и дротиков из метательных машин. Хитроумные журавлеподобные механизмы поднимали своими «клювами « людей и сбрасывали их с высоты. Были машины, способные даже корабли поднять над водой за нос, чтобы затем низвергнуть их в пучину. «Что ж, придётся нам прекратить войну против геометра» — невесело шутил Марцелл. Архимед победил. Он совершил высочайший научный и гражданский подвиг, этот» Главный конструктор» древних Сиракуз. И когда предательство открыло римлянам ворота в город, он погиб как солдат под мечом римского легионера
(Стихотворение читается на фоне музыки Людвига Ван Бетховена « К Элизе»).
Он был задумчив и спокоен,
Над ним невежественный воин
Взмахнул разбойничьим мечом.
Чертил мыслитель с вдохновеньем,
Сдавил лишь сердце тяжкий груз.
« Ужель гореть моим твореньям
И думал Архимед: «Поникну ль
Рукою твёрдой взял он циркуль-
Уж пыль клубилась над дорогой,
То в рабство путь, в ярмо цепей.
«Убей меня, но лишь не трогай,
Никто не знает, кто убийца.
Но знают все, кто был убит!
И через века звучит возглас: «Эврика» для тех , кто ищет и находит.
4, Проверка домашнего задания.
Задача№5. ЕГЭ 2009 (ФФ Лысенко.)
5). Высота цилиндра 6, а радиус основания равен 5. НА окружности основания цилиндра выбраны три точки. А, В и. С так, что А В = В С., А С = 8, угол ABC ЕГЭ 2005-2006 (ФИ ПИ)
18) Концы отрезка АК лежат на окружностях двух оснований цилиндра. Секущая плоскость проходит через точку А и ось цилиндра. Угол между прямой АК и плоскостью основания цилиндра равен 30º, АК=16, площадь боковой поверхности цилиндра равна 80π. Найдите периметр осевого сечения цилиндра.
(2 ученика у доски выполняют домашнюю работу, а в это время все учащиеся решают задачи по готовым чертежам).
5.Решение задач по готовым чертежам .
.
(по материалам ЕГЭ за 2001 – 2012г).
1). Точки К и М лежат на окружностях двух оснований цилиндра. Синус угла наклона прямой К М к плоскости основания цилиндра равен 3/5,
К М = 10, объем цилиндра равен 150π. Найдите площадь осевого сечения цилиндра.
2). Радиус основания цилиндра равен 1, а высота равна 2 6. Отрезки АВ и С D – диаметры одного из оснований цилиндра, а отрезок АА1 – его образующая. Известно что А D = 3. Найдите косинус угла между А1С и В D .
3). Радиус основания цилиндра равен 5, а высота равна 6. Отрезки AB и С D – диаметры одного из оснований цилиндра, отрезок АА1– его образующая. Известно, что В С = 6 2. Найдите синус угол между прямыми А1С и В D .
4). Концы отрезка МК лежат на окружностях двух оснований цилиндра. Угол между прямой МК и плоскостью оснований цилиндра равен 30, МК=8, площадь боковой поверхности цилиндра равен 40π. Найти периметр осевого сечения цилиндра.
5). Высота цилиндра 6, а радиус основания равен 5. НА окружности основания цилиндра выбраны три точки. А, В и. С так, что А В = В С., А С = 8, угол ABC 6). Высота цилиндра равна 12см. Через середину образующей цилиндра проведена прямая, пересекающая ось цилиндра на расстоянии 4 см от нижнего основания. Эта прямая пересекает плоскость, содержащую нижнее основание цилиндра, на расстоянии 18 см от центра нижнего основания. Найдите радиус основания цилиндра.
7) Радиус основания цилиндра равен 6, а высота равна 2. Отрезки АВ и CD – диаметры одного из оснований цилиндра, а отрезок АА1 – его образующая. Известно, что В С=2 21. Найдите синус угла между прямыми А1С и В D .
10). Радиус основания цилиндра равен 1, а высота равна 2√6. Отрезки АВ и С D – диаметры одного из оснований цилиндра, а отрезок АА1 – его образующая. Известно, что AD =√3. Найдите косинус угла между прямыми АС и В D .
11). Точки B и D лежат на окружностях двух оснований цилиндра. Синус угла между прямой BD и плоскостью основания цилиндра равен 0,3, BD =15, объём цилиндра равен π Найдите площадь осевого сечения цилиндра.
12). Точки К и М лежат на окружностях двух оснований цилиндра. Синус угла наклона прямой К М к плоскости основания цилиндра равен 0,6;
К М=10, объём цилиндра равен 150π. Найдите площадь осевого сечения цилиндра.
13) Отрезок АА1 – образующая цилиндра, отрезок АВ – диаметр основания, CD – хорда, перпендикулярная к АВ. Известно, что АА1 =28, А В=16, C D =24 и угол С BD D .
14) Радиус основания цилиндра равен 15, а высота цилиндра равна 16. В окружность основания вписан остроугольный треугольник АВС такой, что ВС=24, и АВ=АС. Отрезки АА1 и ВВ1 – образующие цилиндра. Найдите тангенс угла между плоскостями ВСВ1 и ВА1С.
15) Радиус основания цилиндра равен 6, а высота равна 10. Отрезки АВ и CD – диаметры одного из оснований цилиндра, АС=4√5. Отрезок АА1 – образующая цилиндра. Найдите тангенс угла между прямыми В С и А1 D .
16) Радиус основания цилиндра равен 8, а высота равна 15. Отрезки М N и PQ – диаметры верхнего и нижнего оснований цилиндра, а отрезок ММ1 – образующая цилиндра. Угол между прямыми MN и M 1 P равен 60º. Найдите длину отрезка NQ .
17) Точки М и N расположены на окружностях верхнего и нижнего основания цилиндра, радиус основания которого равен 2, а высота – 3. Длина отрезка MN равна 4. Через отрезок MN проведена плоскость, параллельная образующей цилиндр. Найдите расстояние от оси цилиндра до этой плоскости.
18) Концы отрезка АК лежат на окружностях двух оснований цилиндра. Секущая плоскость проходит через точку А и ось цилиндра. Угол между прямой АК и плоскостью основания цилиндра равен 30º, АК=16, площадь боковой поверхности цилиндра равна 80π. Найдите периметр осевого сечения цилиндра.
19) Через образующую цилиндра проведены две плоскости, пересекающие основание цилиндра: одна – по диаметру АМ, другая – по хорде AD . Угол между этими плоскостями равен 60º. Площадь боковой поверхности цилиндра равна 60π. Найдите площадь сечения цилиндра, проходящего через хорду AD .
20) Через образующую ВС цилиндра проведено сечение BCDE . Объём цилиндра равен 1440π, ВЕ=8, тангенс угла между прямой СЕ и плоскостью основания равен 1,25. Найдите площадь осевого сечения.
21). Цилиндр пересечён плоскостью, параллельной оси и отсекающей от окружностей оснований дуги по 120º. Если высота цилиндра равна 4 см, а радиус основания — 2√3 см, то площадь сечения равна?
22). Радиус основания цилиндра равен 6. Основание ВС равнобедренного треугольника АВС является хордой окружности одного основания этого цилиндра, а вершина С лежит на окружности другого основания. Длина боковой стороны треугольника АВС равна12, а его проекцией на основание цилиндра является правильный треугольник. Найдите площадь осевого сечения цилиндра. (Ответ:72)
23). Высота цилиндра равна 80, а радиус основания – 26. В окружность основания вписан остроугольный треугольник АВС такой, что В С=20,а АВ = АС. Отрезки АА1 и ВВ1 – образующие цилиндра. Найдите котангенс угла между плоскостью СВВ1 и плоскостью ВА1С. (Ответ:1,6)
24). Высота цилиндра равна 40 , а радиус основания 26. В окружность
основания вписан тупоугольный треугольник АВС такой, что В С=20, АВ=АС. Отрезки АА1 и ВВ1 _ образующие цилиндра. Найдите тангенс угла между плоскостью СВВ1 и плоскостью ВА1С. (Ответ:0,05)
Видео:№537. Диаметр основания цилиндра равен 1 м, высота цилиндра равна длинеСкачать
Mn диаметр основания цилиндра mm1 его образующая
Шар вписан в цилиндр. Площадь поверхности шара равна 111. Найдите площадь полной поверхности цилиндра.
Высота цилиндра равна диаметру шара, а радиус основания цилиндра равен радиусу шара (см. рис.).
Площадь основания цилиндра:
Площадь боковой поверхности цилиндра:
Площадь полной поверхности цилиндра:
Поскольку площадь поверхности шара дается формулой имеем:
Высота цилиндра равна 5, а радиус основания 10.
а) Докажите, что площадь боковой поверхности цилиндра равна площади его основания.
б) Найдите площадь сечения цилиндра плоскостью, проходящей параллельно оси цилиндра на расстоянии 6 от неё.
а) Вспомним, что площадь боковой поверхности цилиндра вычисляется по формуле , где — радиус основания, — высота цилиндра. В данном случае , поэтому , откуда и следует требуемое.
б) Сечение цилиндра плоскостью, проходящей параллельно его оси OO1, — прямоугольник ABB1A1 (O и AB — соответственно центр и хорда нижнего основания цилиндра), AA1 = 5. Расстояние от оси цилиндра до плоскости сечения равно высоте OH треугольника OAB. OA = OB = 10, OH = 6, откуда
В условии сказано, что дан цилиндр: «Высота цилиндра. «, а в решении рассмотрен прямой цилиндр. Действительно, ответ такой же получится при решении задачи с наклонным цилиндром, но тем не менее, в сечении образуется параллелограмм, а не прямоугольник: прямая АА1 параллельна и равна прямой ВВ1, как образующие, которые параллельны, в свою очередь оси цилиндра — прямой ОО1. По признаку параллельности прямой и плоскости получаем, что ОО1 параллельна плоскости (АА1ВВ1). И уже нельзя говорить, что ОО1 является высотой, ведь цилиндр может быть и наклонным. Прямая ОО1 является осью цилиндра. А условная прямая О1М может являться высотой цилиндра (точка М может совпасть с точкой О, если цилиндр прямой). Она будет являться и высотой параллелограмма (это может быть и прямоугольник, который по определению также является параллелограммом).
Таким образом, ответ хотя и верный, но рассмотрено частное решение данной задачи. Либо составители допустили ошибку не указав, что дан прямой цилиндр (в 2018-ом же писали: «. образующая перпендикулярна плоскости основания»), либо решение данной задачи следует подправить.
В школьном курсе задачи о наклонных цилиндрах не рассматриваются.
В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки А и В, а на окружности другого основания — точки В1 и С1, причем ВВ1 — образующая цилиндра, а отрезок АС1 пересекает ось цилиндра.
а) Докажите, что угол АВС1 прямой.
б) Найдите площадь боковой поверхности цилиндра, если AB = 20, BB1 = 15, B1C1 = 21.
а) Рассмотрим плоскость, проходящую через ось цилиндра и прямую АС1. Обозначим точку пересечения этой плоскости и окружности основания цилиндра, содержащую точку А, через точку С. Тогда СС1 — образующая цилиндра. Отрезок АС пересекает ось цилиндра. Значит, он проходит через центр окружности основания цилиндра, то есть является ее диаметром. Следовательно, угол АВС прямой.
Прямая СС1 является образующей цилиндра, поэтому она перпендикулярна прямой АВ. Таким образом, прямая АВ перпендикулярна плоскости ВСС1б а значит, угол АВС1 прямой.
б) Отрезок AC является диаметром основания цилиндра. Значит, длина
окружности основания цилиндра равна
Следовательно, площадь боковой поверхности цилиндра равна
В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки А и В, а на окружности другого основания — точки В1 и С1, причем ВВ1 — образующая цилиндра, а отрезок АС1 пересекает ось цилиндра.
а) Докажите, что угол АВС1 прямой.
б) Найдите площадь боковой поверхности цилиндра, если AB = 15, BB1 = 21, B1C1 = 20.
а) Рассмотрим плоскость, проходящую через ось цилиндра и прямую АС1. Обозначим точку пересечения этой плоскости и окружности основания цилиндра, содержащую точку А, через точку С. Тогда СС1 — образующая цилиндра. Отрезок АС пересекает ось цилиндра. Значит, он проходит через центр окружности основания цилиндра, то есть является ее диаметром. Следовательно, угол АВС прямой.
Прямая СС1 является образующей цилиндра, поэтому она перпендикулярна прямой АВ. Таким образом, прямая АВ перпендикулярна плоскости ВСС1б а значит, угол АВС1 прямой.
б) Отрезок AC является диаметром основания цилиндра. Значит, длина
окружности основания цилиндра равна
Следовательно, площадь боковой поверхности цилиндра равна
Аналоги к заданию № 520938: 520945 Все
В прямом кругом цилиндре, осевое сечение которого квадрат со стороной 12, хорда равная перпендикулярна диаметру Найти площадь сечения цилиндра плоскостью если образующая цилиндра.
Из условия задачи следует, что
Если вычислим площадь сегмента то искомую площадь вычислим по формуле где — угол между сечением и плоскостью основания цилиндра, так как сегмент есть ортогональная проекция сечения на основание.
Пусть — центра основания цилиндра, — точка пересечения хорды и диаметра Тогда
Поскольку окружность симметрична относительно диаметра, то
Площадь сегмента вычислим как разность площадей сектора и треугольника
Прежде найдем В (рис.2), где по теореме Пифагора имеем: Итак, катет равен половине гипотенузы названного треугольника, а это значит, что Тогда Из соображений сказанной выше симметрии относительно диаметра
Ортогональная проекция сечения — сегмент
Очевидно, что площадь сегмента CBD равна площади аналогичного сегмента, приведенного в случае 1, т.е.
📺 Видео
Радиус основания цилиндра равен 26, а его образующая равна 9... Найдите площадь сечения.Скачать
РЕШЕНИЕ ЗАДАЧ НА ЦИЛИНДРСкачать
ЕГЭ БАЗА 16 номер Радиус основания цилиндра равен 15, а его образующая равна 14Скачать
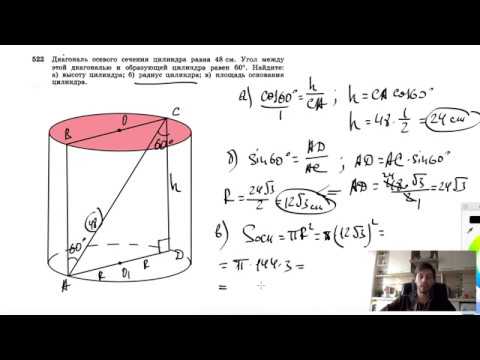
№522. Диагональ осевого сечения цилиндра равна 48 см. Угол между этой диагональю и образующейСкачать
11 класс, 15 урок, Площадь поверхности цилиндраСкачать
Задача 344 Атанасян Геометрия 7 9 2023Скачать
ГЕОМЕТРИЯ 11 класс: Цилиндр. Площадь поверхностиСкачать
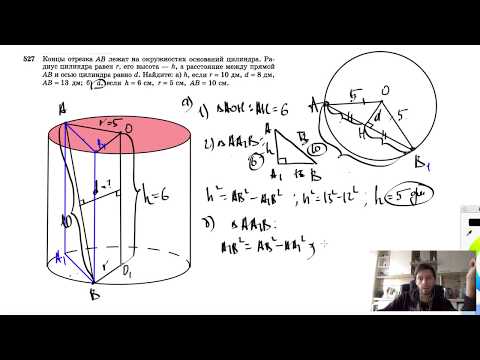
№527. Концы отрезка АВ лежат на окружностях оснований цилиндра. Радиус цилиндра равен г,Скачать
59. Понятие цилиндраСкачать
11 класс, 32 урок, Объем цилиндраСкачать
Цилиндр и конус имеют общее основание и высоту. Высота цилиндра равна радиусу основания... (ЕГЭ)Скачать
Задача 295 Атанасян Геометрия 7 9 2023Скачать
№523. Осевое сечение цилиндра — квадрат, диагональ которого равна 20 см. Найдите: а) высотуСкачать
Профильный ЕГЭ 2024. Вся стереометрия первой части. Задача 3. МиниСИРОПСкачать
11 класс, 14 урок, Понятие цилиндраСкачать
Геометрия 11 класс: Объем призмы и цилиндра. ВидеоурокСкачать
№538. Площадь боковой поверхности цилиндра равна 5. Найдите площадь осевогоСкачать
Объем цилиндра.Скачать
