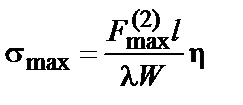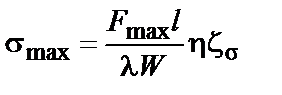Начнем с моментов инерции простых фигур и на их примере выясним для сложных и составных сечений.
Начать объяснение о том, что такое моменты инерции нужно с того, что спросить, а что такое площадь?
Обычная площадь квартиры, огорода сечения стержня? Зачем она и почему?
Так вот площадь это характеристика которую придумали и вывели для разных фигур, чтобы была возможность сравнивать земельные наделы. Не всегда они были прямоугольные или квадратные. А сравнить кто сколько получил в надел было нужно. Вот и вывели такую закономерность для прямоугольника, что если перемножить стороны — получим величину, которую можно будет сравнить с перемноженной высотой на основание деленное пополам для треугольника или для круга Пи умножить на эр в квадрате )). Т.е. площади простых фигур
Что касается моментов инерции в сопротивлении материалов, то тут они появились, когда стало понятно, что есть какая то геометрически измеримая величина для разных форм сечения, которая позволит сравнить сопротивляемость этих сечений изгибу.
Проще говоря бревно, которое выполняет роль балки и изгибается может иметь форму прямоугольника, квадрата или круга, а нам нужно сравнить их сопротивляемость изгибу. Вот для этих целей выводили формулу напряжений и оказалось, что в числителе оказался изгибающий момент, а в знаменателе момент инерции:
Деформированное и не деформированное состояния балки при расчете на изгиб
на балке изображены главные центральные оси z y
прогибы для таких балок будут разными относительно осей z и y, т.к. моменты инерции будут разные.
- Вывод моментов инерции для простых фигур
- Моменты инерции для прямоугольника
- #Сопромат, Моменты инерции. Прямоугольник. Вывод моментов инерции для прямоугольника.
- Моменты инерции для треугольника
- Сопротивление материалов, Моменты инерции для треугольника. Сопромат вывод моментов инерции
- Момент инерции круга. Моменты инерции простых фигур. #сопромат
- Моменты инерции. Оси центральные и главные. Что это и где. #сопромат
- Проверка шинных конструкций с жесткими опорами на электродинамическую стойкость
- 🎦 Видео
Видео:Понимание напряжений в балкахСкачать

Вывод моментов инерции для простых фигур
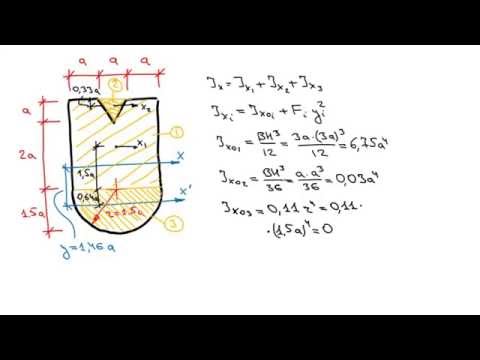
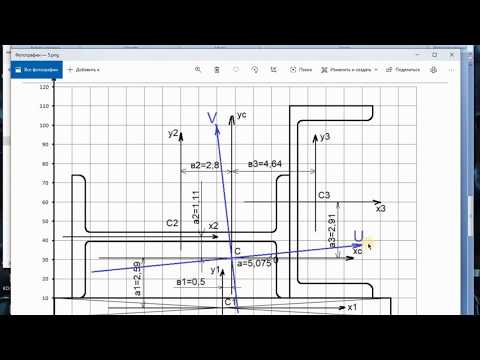
Так вот ниже я приведу видео уроки, плейлист, в котором один за одним выведены моменты инерции для простых фигур, а именно для прямоугольника, треугольника и круга. А затем приводится стандартный расчет моментов инерции для более сложной фигуры, которая состоит из нескольких простых. Всегда сложную фигуру можно разбить на несколько простых. Исходя из этого расчет и ведется.
Моменты инерции измеряются в единицах длины в 4 степени, т.е. см⁴ или м⁴. Чаще всего используется см⁴, т.к. такие единицы измерения приведены в сортаменте прокатной стали.
Момент инерции, это величина, которая показывает сопротивляемость сечения изгибу. На примере линейки хорошо понятно что изгиб в одной плоскости и изгиб в другой плоскости будут сильно отличаться, хотя площадь сечения не меняется. Вот это и было выведено в формуле для напряжений и для прогибов. Что величина, которая сопротивляется изгибающему моменту есть интеграл до координаты центра тяжести площадки в квадрате на площадь элементарной площадки.
Центральными осями называют оси, которые проходят через центр тяжести сечения
Читайте также: Выращивание тыквы в шинах
Главные оси располагаются в сечении таким образом, что центробежный момент относительно них равен нулю. Т.е. это максимальный и минимальный осевые моменты инерции
Оси, которые проходят через центр тяжести сечения и центробежный момент инерции относительно них равен нулю. При этом данные осевые моменты инерции являются экстремальными, т.е. имеют максимальное и минимальное значение. Именно относительно этих осей ведут расчет и к ним приводят нагрузки. Т.е. если какое нибудь внешнее усилие проходит в стороне от главных центральных осей. Это усилие переносят соблюдая правила переноса к главным центральным осям. Только после этого рассматривают действие сил и находят внутренние усилия относительно главных центральных осей инерции.
При вычислении моментов инерции осевых, при переходе от одних осей к другим появляется центробежный момент инерции, как составляющая пары осевых моментов инерции. И только для главных осей центробежные моменты инерции равны нулю. Именно эти оси мы и отыскиваем в наших расчетах. Поэтому мы ищем величину центробежного момента инерции для не главных осей и из свойства, что главные центральные оси это такие оси, относительно которых центробежный момент инерции равен нулю, находим положение главных центральных осей.
Видео:Основы Сопромата. Геометрические характеристики поперечного сеченияСкачать

Моменты инерции для прямоугольника
Видео:Момент инерцииСкачать

#Сопромат, Моменты инерции. Прямоугольник. Вывод моментов инерции для прямоугольника.
Сопротивление материалов и Моменты инерции для прямоугольника. Понятие моментов инерции, формулы и вывод для прямоугольника. Осевые центробежный моменты инерции. для треугольника вывод моментов инерции в этом видео: https://www.youtube.com/embed/_pixohVoc-4?vq=hd720 Тема моментов инерции возникла в связи стем, что для определения напряжений при изгибе понадобилась геометрическая характеристика, которая сопротивляется внутреннему усилию (изгибающему моменту). В результате вывода формулы напряжений и появилась эта формула, выраженная через интеграл от квадрата координаты помноженной на площадь элементарной площадки. Эту геометрическую характеристику и назвали моментом инерции. пройти полный курс обучения сопромату и строймеху онлайн, по скайпу. Задать вопросы можно: — через сайт: https://stroymex.online — skype: zabolotnyiAN — email: zabolotnyiAN@gmail.com — комменты к видео — Телеграм https://t.me/AleksanderCrafts Телеграм канал: https://t.me/sroymexOnline Не тратьте время зря, задавайте вопросы. Узнайте стоимость обучения: https://stroymex.online/usloviya-i-tsena-onlayn-obucheniya-sopromat-i-stroymeh Получите первую консультацию бесплатно! Facebook: https://www.facebook.com/SopromatOnline
2018-04-09
моменты инерции для прямоугольника для главных центральных осей равны, формула
моменты инерции для прямоугольника для осей проходящих через основные размеры равны, формула
Моменты инерции для треугольника
Видео:Как определить сечение провода.Скачать

Сопротивление материалов, Моменты инерции для треугольника. Сопромат вывод моментов инерции
Сопротивление материалов и Моменты инерции для треугольника. Сопромат вывод моментов инерции для простых фигур. Моменты инерции для треугольника. Моменты инерции для осей в треугольнике, которые проходят через основные размеры. Вывод и пояснение к этой теме сопротивления материалов. для прямоугольника вывод моментов инерции в этом видео: https://www.youtube.com/watch?v=v1TE1UW_sRE&feature=youtu.be Тема моментов инерции возникла в связи стем, что для определения напряжений при изгибе понадобилась геометрическая характеристика, которая сопротивляется внутреннему усилию (изгибающему моменту). В результате вывода формулы напряжений и появилась эта формула, выраженная через интеграл от квадрата координаты помноженной на площадь элементарной площадки. Эту геометрическую характеристику и назвали моментом инерции. пройти полный курс обучения сопромату и строймеху онлайн, по скайпу Задать вопросы можно: — через сайт: https://stroymex.online — skype: zabolotnyiAN — email: zabolotnyiAN@gmail.com — комменты к видео — Телеграм https://t.me/AleksanderCrafts Телеграм канал: https://t.me/sroymexOnline Не тратьте время зря, задавайте вопросы. Узнайте стоимость обучения: https://stroymex.online/usloviya-i-tsena-onlayn-obucheniya-sopromat-i-stroymeh Получите первую консультацию бесплатно! Facebook: https://www.facebook.com/SopromatOnline
Читайте также: Шины farroad frd66 характеристики
2018-04-09
Моменты инерции треугольника относительно произвольых осей
Моменты инерции треугольника относительно центральных осей
Видео:Моменты инерции сечения из простых фигурСкачать

Момент инерции круга. Моменты инерции простых фигур. #сопромат
Вывод моментов инерции для круга. Видео урок из темы «Моменты инерции простых фигур». В видео приведен вывод момента инерции полярного, в полярной системе координат Ip Затем выведены моменты инерции осевые Iz, Iy. Задать вопросы можно: — через сайт: https://stroymex.online — skype: zabolotnyiAN — email: zabolotnyiAN@gmail.com — комменты к видео — Телеграм https://t.me/AleksanderCrafts Телеграм канал: https://t.me/sroymexOnline Не тратьте время зря, задавайте вопросы. Узнайте стоимость обучения: https://stroymex.online/usloviya-i-tsena-onlayn-obucheniya-sopromat-i-stroymeh Получите первую консультацию бесплатно! Facebook: https://www.facebook.com/SopromatOnline
2019-09-14
Видео:Теория (часть 1) осевые моменты инерцииСкачать

Моменты инерции. Оси центральные и главные. Что это и где. #сопромат
Центральные оси — любая пара взаимно перпендикулярных осей, которые проходят через центр тяжести фигуры Главные оси — оси для которых центробежный момент инерции равен нулю, а осевые моменты имеют максимум и минимум. Об этом и многом другом в видео уроке по моментам инерции в сопротивлении материалов Задать вопросы можно: — через сайт: https://stroymex.online — skype: zabolotnyiAN — email: zabolotnyiAN@gmail.com — комменты к видео — Телеграм https://t.me/AleksanderCrafts Телеграм канал: https://t.me/sroymexOnline Не тратьте время зря, задавайте вопросы. Узнайте стоимость обучения: https://stroymex.online/usloviya-i-tsena-onlayn-obucheniya-sopromat-i-stroymeh Получите первую консультацию бесплатно! Facebook: https://www.facebook.com/SopromatOnline
2019-09-14
Видео:Техническая механика/Определение общих осевых моментов инерции сложносоставного сечения.Скачать

Проверка шинных конструкций с жесткими опорами на электродинамическую стойкость
7.3.3.1. Шинную конструкцию, изоляторы которой обладают высокой жесткостью и неподвижны при КЗ, при расчете следует представлять как стержень с защемленными концами, имеющий основную частоту собственных колебаний.
Рис. 7.4. Двухполосная шина
Формулы для определения момента инерции J
и момента сопротивления W поперечных сечений шин
| Сечения шин | Расчетные формулы | |
| J, м 4 | W, м 3 | |
 |  |  |
 | 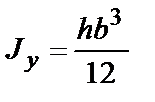 |  |
 |  | 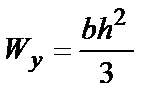 |
 |  |  |
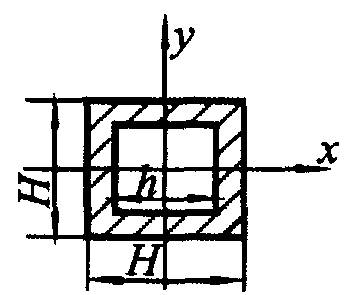 | 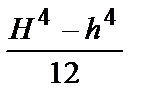 | 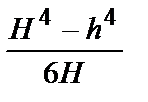 |
 |  |  |
 |  |  |
 | 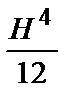 |  |
 | 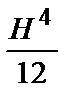 | 0,118Н 3 |
 | 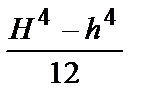 | 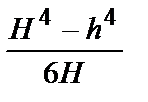 |
 | Для одного элемента  ; ;  | |
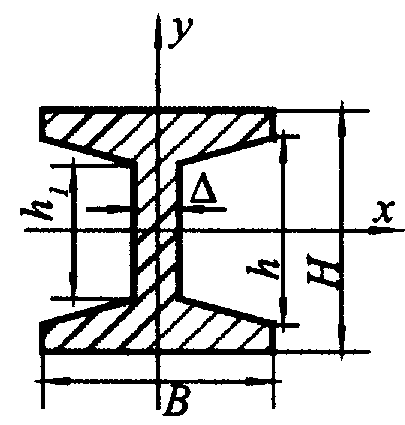 |  ; ;  ; ;  ; ;  ; a»1/6 для стандартных двутавровых профилей ; a»1/6 для стандартных двутавровых профилей | |
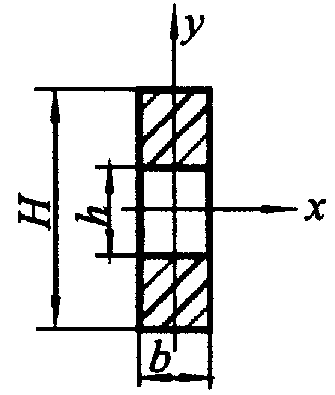 |  ; ; 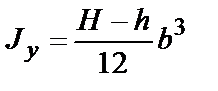 |  ; ;  |
| Сечение прокатных профилей стандартных размеров | Приближенные формулы: двутавровый профиль на «ребро»  швеллерообразный (корытный) профиль на «ребро» швеллерообразный (корытный) профиль на «ребро»  | |
| Сечение любой формы | Ориентировочная оценка момента сопротивления относительно центральной оси: для сплошного симметричного сечения  ; ;  ; для полого симметричного сечения ; для полого симметричного сечения  ; ; 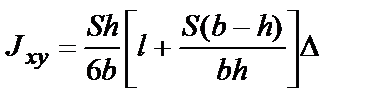 ; где S — площадь сечения; h, b — высота и ширина сечения соответственно; l — длина периметра; D — толщина стенки (для полого сечения) ; где S — площадь сечения; h, b — высота и ширина сечения соответственно; l — длина периметра; D — толщина стенки (для полого сечения) |
* Если прокладки приварены к обеим полосам пакета, моменты инерции и момент сопротивления принимаются равными: 

7.3.3.2. Максимальное напряжение в материале шин и нагрузку на изоляторы шинной конструкции, в которой шины расположены в одной плоскости, а изоляторы обладают высокой жесткостью, следует определять по формулам:
Читайте также: Шина для лечебной иммобилизации это
(7.19)
, (7.20)
(7.21)
, (7.22)
где h — коэффициент динамической нагрузки, зависящий от расчетной основной частоты собственных колебаний шины f1. Значения коэффициента для двухфазного и трехфазного КЗ в зависимости от отношения f1/fc (fc = 50 Гц) следует определять по графику на рис. 7.5.
Значения расчетной частоты собственных колебаний (f1) в герцах следует определять в соответствии с п. 7.3.3.4.
7.3.3.3. Максимальные нагрузки на проходные изоляторы следует определять по формуле
, (7.23)
где lпр — расстояние от торца проходного изолятора до ближайшего опорного изолятора фазы, м.
7.3.3.4. Расчетную частоту собственных колебаний шины в герцах следует определять по формуле
, (7.24)
где Е — модуль упругости материала шины, Па;
J — момент инерции поперечного сечения шины, м 4 ;
т — масса шины на единицу длины, кг/м;
r1 — параметр основной собственной частоты шины.
Значения параметра частоты зависят от типа шинной конструкции и представлены в табл. 7.1.
7.3.3.5. Максимальное напряжение в материале составных шин следует определять по формуле
где sф.max — максимальное напряжение в материале шин, которое следует определять в зависимости от вида КЗ по формуле (7.19) или (7.21);
sэл.max — максимальное напряжение в материале шины, которое следует определять по формуле
, (7.26)
где hэл — коэффициент динамической нагрузки, зависящий от основной частоты (f1эл) собственных колебаний элементов составной шины, который следует определять по расчетному графику, приведенному на рис. 7.5.
Рис. 7.5. Зависимость динамического коэффициента для изоляторов и шин от частоты собственных колебаний шины, где 1 при Куд ³ 1,60; 2 при Куд = 1,40;
Расчетную основную частоту собственных колебаний элементов составной шины фазы в герцах следует определять по формуле
, (7.27)
где lэл — длина пролета элемента шины между прокладками, м;
Jэл — момент инерции поперечного сечения элемента шин, м 4 ;
тэл — масса элемента на единицу длины, кг/м;
аэл — расстояние между осями элементов составных шин (рис. 7.4), м.
7.3.3.6. Максимальные напряжения в материале шин и максимальные нагрузки на опорные и проходные изоляторы при расположении шин по вершинам треугольника (рис. 7.2, б, в, г) следует определять с учетом их пространственных колебаний по формулам
; (7.28)
; (7.29)
, (7.30)
где W — меньший из двух моментов сопротивлений поперечного сечения шины (момента сопротивления WJ при изгибе в плоскости J и момента сопротивления Wt при изгибе шины в плоскости t) (рис. 7.2), м 3 ;


zs, zF — коэффициенты, значения которых для наиболее распространенных типов шинных конструкций (рис. 7.2, б, в, г) приведены в табл. 7.5.
Значения коэффициентов zs и zF шинных конструкций
- Свежие записи
- Нужно ли менять пружины при замене амортизаторов
- Скрипят амортизаторы на машине что делать
- Из чего состоит стойка амортизатора передняя
- Чем стянуть пружину амортизатора без стяжек
- Для чего нужны амортизаторы в автомобиле
🎦 Видео
Определение осевых моментов инерции составного несимметричного сечения. СопроматСкачать
Урок 94. Вычисление моментов инерции телСкачать
Основы сопромата. Задача 4. Момент инерции сложного сеченияСкачать
Момент инерцииСкачать
Как понять, когда протектор износился и шины пора менятьСкачать
7. Подбор сечения при изгибе ( практический курс по сопромату )Скачать
Понимание сопротивления качению!Скачать
У ВАС НЕПРАВИЛЬНОЕ ДАВЛЕНИЕ В ШИНАХ! ТОП-7 дорогих ошибок при проверке давления в шинах!Скачать
Лабораторная работа №2. Определение момента инерции махового колесаСкачать
Измеряем и проверяем остаточную глубину протектора специальнам измерителем СВОИМИ СИЛАМИСкачать
Радиус инерции. Момент сопротивленияСкачать
Определение положения главных центральных осей и главных центральных моментов инерцииСкачать
9.2. Геометрические характеристики плоских сечений. Моменты инерции плоских сеченийСкачать