Момента инерции шин прямоугольного сечения

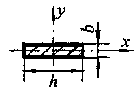
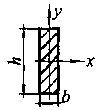
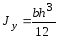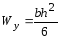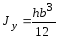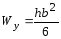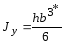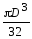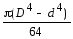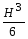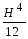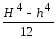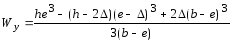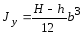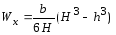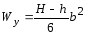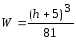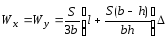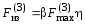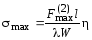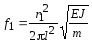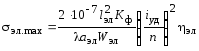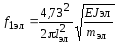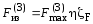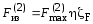Наибольшее удельное усилие при трехфазном КЗ Н/м определяется по формуле:

где i (3)2 _y – ударный ток КЗ;

а_ф – расстояние между фазами, которое составляет 1…2 м при напряжениях 6…10 кВт.

Т.к. расстояние между фазами значительно больше периметра шин а>>2(b+h), то коэффициент формы принят k_ф=1. Наибольшие электродинамические усилия возникают при трехфазном КЗ, поэтому в расчетах учитывается ударный ток трехфазного КЗ (i_y (3) ). Индексы (3) для упрощения опускаются.

Равномерно распределенная сила f создает изгибающий момент, : , (30.6)

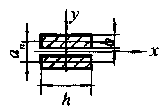
где _пи — длина пролета между опорными изоляторами шинной конструкции, м;

— шина рассматривается как многопролетная балка, свободно лежащая на опорах.

Напряжение в материале шины, возникающее при воздействии изгибающего момента, МПа :

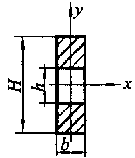
где W – момент сопротивления шины относительно оси, перпендикулярной действию усилия, см 3 ; зависит от размеров, формы и расположения шин.

Шины механически прочны, если

где — допустимое механическое напряжение в материале шин.

Для алюминиевых шин

Механический расчет двухполосных шин

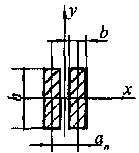
Если каждая фаза выполняется из двух полос, то возникают усилия между полосами и между фазами. Усилие между полосами не должно приводить к их соприкосновению. Для того, чтобы уменьшить это усилие, в пролете между полосами устанавливают прокладки.

Пролет между прокладками _n выбирается таким образом, чтобы электродинамические силы, возникающие при КЗ, не вызывали соприкосновения полос

Механическая система две полосы – изоляторы должны иметь частоту собственных колебаний больше 200 Гц, чтобы не произошло резкого увеличения усилия в результате механического резонанса.

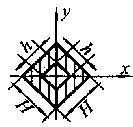
Схема крепления двухполосных шин. График изменения коэффициента формы

Исходя из этого, величина _n выбирается еще по одному условию:

В последних двух формулах:

a_n – расстояние между осями полос, см;

J_n = — момент инерции полосы, см 4 ;

K_ф – коэффициент формы (рисунок 4);

m_n – масса полосы на единицу длины, кг/м;

E – модуль упругости материала (таблица 30.2).

В расчет принимается меньшая из двух l_n величин, определенных по этим формулам.

Таблица 30.2.

Читайте также: Зимние шины yokohama 165

Силу взаимодействия между полосами в пакете из двух полос можно найти по формуле:

где b – толщина полос.

Напряжение в материале шин от взаимодействия полос, МПа:

, (30.11)

где W_n – момент сопротивления одной полосы, см 3 ;

– расстояние между прокладками, м.

Напряжение в материале шин от взаимодействия фаз определяется по формуле :

где _пи – длина пролета между изоляторами, м;

W_ф – момент сопротивления пакета шин , см 3 ;

а_ф – расстояние между осями фаз.

Шины механически прочны, если:

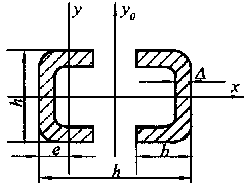
Механический расчет шин коробчатого сечения (Рисунок 30.5)

Шины коробчатого сечения имеют значительно больший момент инерции, чем шины прямоугольного сечения. Например, шина (100 ) мм 2 при расположении на ребро имеет

а одна шина швеллерного профиля сечением 10 мм 2 имеет

Соответственно, при расположении прямоугольной шины плашмя

Следовательно, в шинах коробчатого сечения частота собственных колебаний значительно больше (cм. выше для f₀), чем для шин прямоугольного сечения. Это позволяет производить расчет без учета механических колебаний. Если шины расположены в горизонтальной плоскости (рисунок 30.5,а) и швеллеры соединены жестко между собой, то .

При отсутствии жесткого соединения W_ф = 2W_у-у.

Если шины расположены в вертикальной плоскости (рисунок 30.5,б), то W_ф = 2W_x—x.

Напряжение в материале шин от взаимодействия фаз определяется по формуле (30.12):

В данном случае можно принять l_пи = 0,5 … 1,5м.

Видео:Геометрические характеристики. Моменты инерции. Радиусы инерции. Сопромат.Скачать

Онлайн калькулятор по расчету характеристик прямоугольного сечения

Калькулятор онлайн рассчитывает геометрические характеристики (площадь, моменты инерции, моменты сопротивления изгибу, радиусы инерции) плоского сечения в виде прямоугольника по известным линейным размерам и выводит подробное решение.

Видео:Сопротивление материалов. Лекция: геометрические характеристики сечений - моменты инерцииСкачать

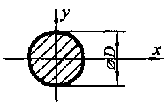
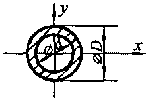
Формулы для определения момента инерции j и момента сопротивления w поперечных сечений шин

;

;

;

;

;

a»1/6 для стандартных двутавровых профилей

;

;

Сечение прокатных профилей стандартных размеров

двутавровый профиль на «ребро»

швеллерообразный (корытный) профиль на «ребро»

Ориентировочная оценка момента сопротивления относительно центральной оси:

для сплошного симметричного сечения

; ;

для полого симметричного сечения

;

;

где S — площадь сечения; h, b — высота и ширина сечения соответственно; l — длина периметра; D — толщина стенки (для полого сечения)

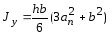
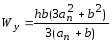
* Если прокладки приварены к обеим полосам пакета, моменты инерции и момент сопротивления принимаются равными: и .

7.3.3.2. Максимальное напряжение в материале шин и нагрузку на изоляторы шинной конструкции, в которой шины расположены в одной плоскости, а изоляторы обладают высокой жесткостью, следует определять по формулам:

(7.19)

, (7.20)

(7.21)

, (7.22)

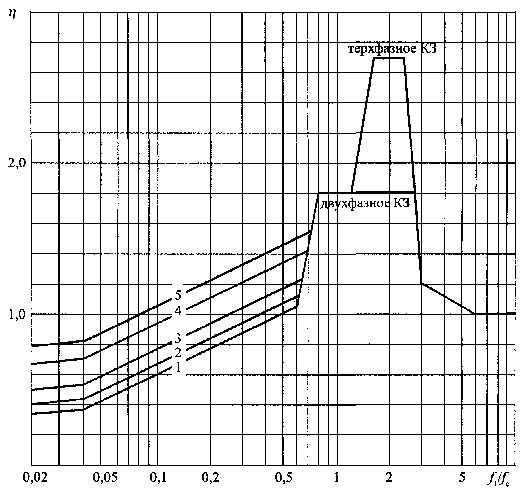
где h — коэффициент динамической нагрузки, зависящий от расчетной основной частоты собственных колебаний шины f₁. Значения коэффициента для двухфазного и трехфазного КЗ в зависимости от отношения f₁/f_c (f_c = 50 Гц) следует определять по графику на рис. 7.5.

Значения расчетной частоты собственных колебаний (f₁) в герцах следует определять в соответствии с п. 7.3.3.4.

7.3.3.3. Максимальные нагрузки на проходные изоляторы следует определять по формуле

, (7.23)

где l_пр — расстояние от торца проходного изолятора до ближайшего опорного изолятора фазы, м.

7.3.3.4. Расчетную частоту собственных колебаний шины в герцах следует определять по формуле

, (7.24)

где Е — модуль упругости материала шины, Па;

J — момент инерции поперечного сечения шины, м 4 ;

т — масса шины на единицу длины, кг/м;

r₁ — параметр основной собственной частоты шины.

Значения параметра частоты зависят от типа шинной конструкции и представлены в табл. 7.1.

7.3.3.5. Максимальное напряжение в материале составных шин следует определять по формуле

где s_ф.max — максимальное напряжение в материале шин, которое следует определять в зависимости от вида КЗ по формуле (7.19) или (7.21);

s_эл.max — максимальное напряжение в материале шины, которое следует определять по формуле

, (7.26)

где h_эл — коэффициент динамической нагрузки, зависящий от основной частоты (f_1эл) собственных колебаний элементов составной шины, который следует определять по расчетному графику, приведенному на рис. 7.5.

Рис. 7.5. Зависимость динамического коэффициента для изоляторов и шин от частоты собственных колебаний шины, где 1 при К_уд ³ 1,60; 2 при К_уд = 1,40;

Расчетную основную частоту собственных колебаний элементов составной шины фазы в герцах следует определять по формуле

, (7.27)

где l_эл — длина пролета элемента шины между прокладками, м;

J_эл — момент инерции поперечного сечения элемента шин, м 4 ;

т_эл — масса элемента на единицу длины, кг/м;

а_эл — расстояние между осями элементов составных шин (рис. 7.4), м.

7.3.3.6. Максимальные напряжения в материале шин и максимальные нагрузки на опорные и проходные изоляторы при расположении шин по вершинам треугольника (рис. 7.2, б, в, г) следует определять с учетом их пространственных колебаний по формулам

; (7.28)

; (7.29)

, (7.30)

где W — меньший из двух моментов сопротивлений поперечного сечения шины (момента сопротивления W_J при изгибе в плоскости J и момента сопротивления W_t при изгибе шины в плоскости t) (рис. 7.2), м 3 ;

, — электродинамические силы, определяемые соответственно по формулам (7.10) и (7.11);

z_s, z_F — коэффициенты, значения которых для наиболее распространенных типов шинных конструкций (рис. 7.2, б, в, г) приведены в табл. 7.5.

• Свежие записи
  • Нужно ли менять пружины при замене амортизаторов
  • Скрипят амортизаторы на машине что делать
  • Из чего состоит стойка амортизатора передняя
  • Чем стянуть пружину амортизатора без стяжек
  • Для чего нужны амортизаторы в автомобиле

  🎬 Видео

  Моменты инерции Прямоугольника ► Вывод моментов инерции для прямоугольникаСкачать

  

  Теория (часть 1) осевые моменты инерцииСкачать

  

  7. Момент инерции треугольника и конусаСкачать

  

  Момент инерцииСкачать

  

  Урок 98. Задачи на вычисление моментов инерции (ч.1)Скачать

  

  Моменты инерции простейших фигур. Оси центральные и главные. Что это и где. #сопроматСкачать

  

  Основы Сопромата. Геометрические характеристики поперечного сеченияСкачать

  

  Моменты инерции для треугольника. Вывод моментов инерции для треугольниковСкачать

  

  Основы сопромата. Задача 4. Момент инерции сложного сеченияСкачать

  

  Урок 94. Вычисление моментов инерции телСкачать

  

  5. Момент инерции простейших телСкачать

  

  Расчет момента инерции тонкого стержняСкачать

  

  Расчет момента инерции шараСкачать

  

  Расчет момента инерции цилиндраСкачать

  

  Момент инерции шара и сферы. Как интегрировать "на пальцах"?Скачать

  

  Момент инерции круга. Моменты инерции простых фигур. #сопроматСкачать

  

  Конструкция ЦМК (шина с цельнометаллическим кордом). Радиальная грузовая шина. Основные элементы.Скачать

  

  Механика | динамика | вращательное движение | момент инерции диска | для взрослыхСкачать