- Oo1 ось цилиндра aa1b1b осевое сечение цилиндра найти высоту цилиндра
- Презентация по геометрии на тему «Цилиндр. Сечения цилиндра»
- Дистанционное обучение как современный формат преподавания
- Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Математика: теория и методика преподавания в образовательной организации
- Оставьте свой комментарий
- Подарочные сертификаты
- Цилиндры
- Основные определения и свойства цилиндра
- Сечения цилиндра
- Объем цилиндра. Площадь боковой поверхности цилиндра. Площадь полной поверхности цилиндра
- Oo1 ось цилиндра aa1b1b осевое сечение цилиндра найти высоту цилиндра
- Oo1 ось цилиндра aa1b1b осевое сечение цилиндра найти высоту цилиндра
- 📺 Видео
Видео:Задача на вычисление высоты цилиндраСкачать

Oo1 ось цилиндра aa1b1b осевое сечение цилиндра найти высоту цилиндра
Высота цилиндра равна 3, а радиус основания равен 13.
а) Постройте сечение цилиндра плоскостью, проходящей параллельно оси цилиндра, так, чтобы площадь этого сечения равнялась 72.
б) Найдите расстояние от плоскости сечения до центра основания цилиндра.
а) Пусть OO1 — ось цилиндра. Проведем AB и CD параллельно оси цилиндра. Проведем BD и AC. Так как через две параллельные прямые проходит единственная плоскость, то прямоугольник BDCA — искомое сечение (см. рис.).
б) В этом прямоугольнике одна сторона будет равняться высоте цилиндра, а вторая — хорде окружности, лежащей в основании. Так как то где x — хорда AC. Проведем OH перпендикулярно AC. В силу того, что треугольник ACO равнобедренный, точка H также будет являться серединой AC. Тогда из прямоугольного треугольника, у которого гипотенуза — радиус OC, а один катет — половина этой хорды, находим второй катет OH по теореме Пифагора.
Таким образом, расстояние от центра окружности до сечения равно 5.
при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки,
Видео:№525. Площадь осевого сечения цилиндра равна 10 м2, а площадь основания — 5 м2.Скачать

Презентация по геометрии на тему «Цилиндр. Сечения цилиндра»
Ищем педагогов в команду «Инфоурок»
Описание презентации по отдельным слайдам:
Пособие по геометрии для 11 класса Составила Учитель математики СШ №115 г. Донецка Корсун Людмила Николаевна
Цилиндром (круговым цилиндром) называется тело, состоящее из двух кругов, которые не лежат в одной плоскости, а совмещаются параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих кругов.
Круги – основания цилиндра. Отрезки, соединяющие соответствующие точке окружностей кругов, — образующие. AB – образующая цилиндра. Цилиндр называется прямым, если его образующие перпендикулярны плоскостям оснований. O1A – радиус основания цилиндра.
Свойства цилиндра Основания цилиндра равны и параллельны. Образующие цилиндра параллельны и равны. AA1=BB1 Высота цилиндра (расстояние между плоскостями оснований) равна образующей. Hцил. = AA1 = OO1
При вращении прямоугольника около его стороны как оси образуется цилиндр. AA1 O1O – прямоугольник. OO1 – ось образованного цилиндра.(OO1 || AA1) Rцил. = OA = O1A1
Площадь поверхности и объем цилиндра
Сечения цилиндра плоскостями. Осевое сечение цилиндра. AA1 B1B – осевое сечение (сечение, проходящее через ось цилиндра OO1) AA1 B1B – прямоугольник (если AA1 B1B – квадрат, то цилиндр называется равносторонним). AB = dосн. = 2R; AA1 = Hцил.
Сечение цилиндра плоскостью, параллельной его оси. (ABC) || OO1; ABCD – прямоугольник; AB и CD – образующие цилиндра; AB = Hцил.
Сечение цилиндра плоскостью, параллельной его оси Плоскость, параллельная плоскости основания цилиндра, пересекает его боковую поверхность по окружности основания. Rпер. = Rцил.
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
Международная дистанционная олимпиада Осень 2021
Вам будут интересны эти курсы:
Оставьте свой комментарий
Минтруд предложил проект по реабилитации детей-инвалидов
Школьников не планируют переводить на удаленку после каникул
В школе в Пермском крае произошла стрельба
Минобрнауки утвердило перечень олимпиад для школьников на 2021-2022 учебный год
Минобразования Кузбасса рекомендовало техникумам и школам уйти на каникулы до 7 ноября
В Москве стартует онлайн-чемпионат для школьников Soft Skills — 2035
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Видео:№523. Осевое сечение цилиндра — квадрат, диагональ которого равна 20 см. Найдите: а) высотуСкачать

Цилиндры
Видео:№529. Высота цилиндра равна 8 см, радиус равен 5 см. Найдите площадь сечения цилиндраСкачать

Основные определения и свойства цилиндра
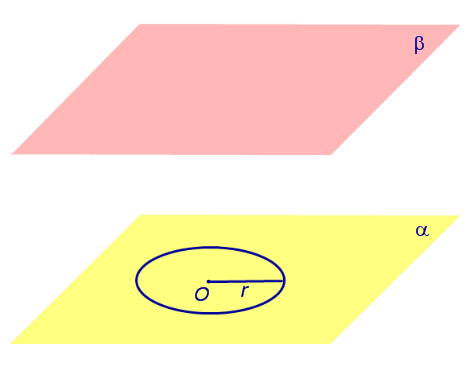
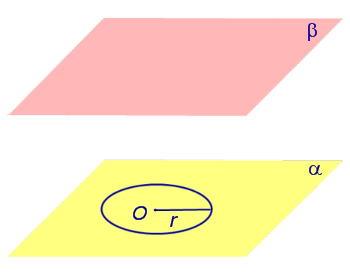
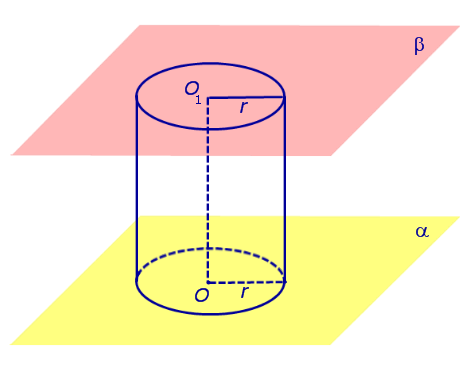
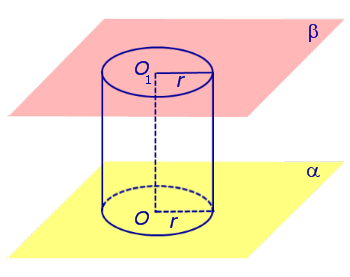
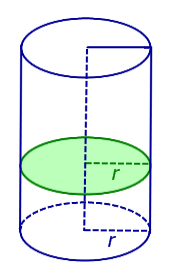
Если из каждой точки окружности опустить перпендикуляр на плоскость β , то основания этих перпендикуляров образуют на плоскости β окружность радиуса r , центр O1 которой является основанием перпендикуляра, опущенного из точки O на плоскость β (рис.2).
Отрезок перпендикуляра, опущенного из любой точки окружности с центром O на плоскость β , который заключен между плоскостями α и β , называют образующей цилиндра .
Совокупность всех образующих цилиндра называют цилиндрической поверхностью .
Фигуру, ограниченную цилиндрической поверхностью и плоскостями α и β, называют цилиндром .
Отрезок OO1 называют осью цилиндра .
Радиус окружности Радиус окружности на плоскости α с центром в точке O называют радиусом цилиндра .
Круги с центрами O и O1 на плоскостях α и β , называют основаниями цилиндра .
Замечание 1. Цилиндрическую поверхность часто называют боковой поверхностью цилиндра . Боковая поверхность цилиндра и основания цилиндра вместе составляют полную поверхность цилиндра .
Замечание 2. Каждая образующая цилиндра параллельна оси цилиндра, а длина каждой образующей цилиндра равна высоте цилиндра.
Замечание 3. Прямая OO1 является осью симметрии цилиндра, а середина отрезка OO1 является центром симметрии цилиндра.
Видео:Видеоурок по математике "Цилиндр"Скачать

Сечения цилиндра
Определение 2. Сечением цилиндра называют пересечение цилиндра с плоскостью.
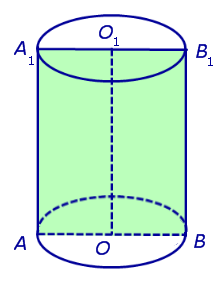
Если сечение проходит через ось цилиндра, то такое сечение называют осевым сечением цилиндра (рис. 3).
На рисунке 3 изображено одно из осевых сечений цилиндра – прямоугольник AA1B1B .
Замечание 4. Каждое осевое сечение цилиндра с радиусом r и высотой h является прямоугольником со сторонами 2r и h .
Определение 3. Перпендикулярным сечением цилиндра называют сечение, перпендикулярное оси цилиндра (рис. 4).
Замечание 5. Любым перпендикулярным сечением цилиндра будет круг радиуса r .
Замечание 6. Более подробно случаи взаимного расположения цилиндра и плоскости рассматриваются в разделе нашего справочника «Взаимное расположение цилиндра и плоскости в пространстве».
Видео:11 класс. Геометрия. Объем цилиндра. 14.04.2020Скачать

Объем цилиндра. Площадь боковой поверхности цилиндра.
Площадь полной поверхности цилиндра
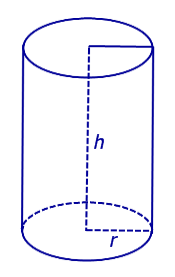
Для цилиндра с радиусом r и высотой h (рис. 5)
введем следующие обозначения
| V | объем цилиндра |
| Sбок | площадь боковой поверхности цилиндра |
| Sполн | площадь полной поверхности цилиндра |
| Sосн | площадь основания цилиндра |
Тогда справедливы следующие формулы для вычисления объема, площади боковой и полной поверхности цилиндра:
при помощи предельного перехода, когда число сторон правильной призмы n неограниченно возрастает. Однако доказательство этого факта выходит за рамки школьной программы.
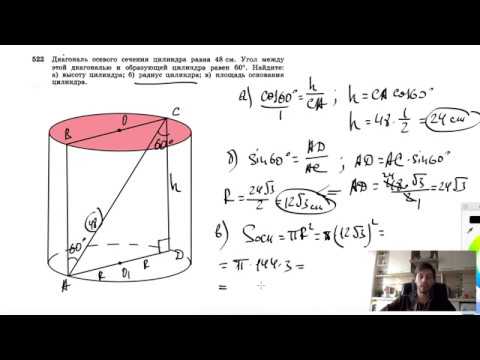
Видео:№522. Диагональ осевого сечения цилиндра равна 48 см. Угол между этой диагональю и образующейСкачать
Oo1 ось цилиндра aa1b1b осевое сечение цилиндра найти высоту цилиндра
Высота цилиндра равна 3, а радиус основания равен 13.
а) Постройте сечение цилиндра плоскостью, проходящей параллельно оси цилиндра, так, чтобы площадь этого сечения равнялась 72.
б) Найдите расстояние от плоскости сечения до центра основания цилиндра.
а) Пусть OO1 — ось цилиндра. Проведем AB и CD параллельно оси цилиндра. Проведем BD и AC. Так как через две параллельные прямые проходит единственная плоскость, то прямоугольник BDCA — искомое сечение (см. рис.).
б) В этом прямоугольнике одна сторона будет равняться высоте цилиндра, а вторая — хорде окружности, лежащей в основании. Так как то где x — хорда AC. Проведем OH перпендикулярно AC. В силу того, что треугольник ACO равнобедренный, точка H также будет являться серединой AC. Тогда из прямоугольного треугольника, у которого гипотенуза — радиус OC, а один катет — половина этой хорды, находим второй катет OH по теореме Пифагора.
Таким образом, расстояние от центра окружности до сечения равно 5.
при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки,
Видео:№537. Диаметр основания цилиндра равен 1 м, высота цилиндра равна длинеСкачать

Oo1 ось цилиндра aa1b1b осевое сечение цилиндра найти высоту цилиндра
Высота цилиндра равна 5, а радиус основания 10.
а) Докажите, что площадь боковой поверхности цилиндра равна площади его основания.
б) Найдите площадь сечения цилиндра плоскостью, проходящей параллельно оси цилиндра на расстоянии 6 от неё.
а) Вспомним, что площадь боковой поверхности цилиндра вычисляется по формуле , где — радиус основания, — высота цилиндра. В данном случае , поэтому , откуда и следует требуемое.
б) Сечение цилиндра плоскостью, проходящей параллельно его оси OO1, — прямоугольник ABB1A1 (O и AB — соответственно центр и хорда нижнего основания цилиндра), AA1 = 5. Расстояние от оси цилиндра до плоскости сечения равно высоте OH треугольника OAB. OA = OB = 10, OH = 6, откуда
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получен верный ответ. | 2 |
| Решение содержит обоснованный переход к планиметрической задаче, но получен неверный ответ или решение не закончено, или при правильном ответе решение недостаточно обосновано. | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 2 |
В условии сказано, что дан цилиндр: «Высота цилиндра. «, а в решении рассмотрен прямой цилиндр. Действительно, ответ такой же получится при решении задачи с наклонным цилиндром, но тем не менее, в сечении образуется параллелограмм, а не прямоугольник: прямая АА1 параллельна и равна прямой ВВ1, как образующие, которые параллельны, в свою очередь оси цилиндра — прямой ОО1. По признаку параллельности прямой и плоскости получаем, что ОО1 параллельна плоскости (АА1ВВ1). И уже нельзя говорить, что ОО1 является высотой, ведь цилиндр может быть и наклонным. Прямая ОО1 является осью цилиндра. А условная прямая О1М может являться высотой цилиндра (точка М может совпасть с точкой О, если цилиндр прямой). Она будет являться и высотой параллелограмма (это может быть и прямоугольник, который по определению также является параллелограммом).
Таким образом, ответ хотя и верный, но рассмотрено частное решение данной задачи. Либо составители допустили ошибку не указав, что дан прямой цилиндр (в 2018-ом же писали: «. образующая перпендикулярна плоскости основания»), либо решение данной задачи следует подправить.
В школьном курсе задачи о наклонных цилиндрах не рассматриваются.
📺 Видео
Радиус основания цилиндра равен 26, а его образующая равна 9... Найдите площадь сечения.Скачать

11 класс, 32 урок, Объем цилиндраСкачать

№521. Докажите, что осевое сечение цилиндра является прямоугольником, две противоположныеСкачать

11 класс, 15 урок, Площадь поверхности цилиндраСкачать

Объем цилиндра.Скачать

Нахождение площади боковой поверхности цилиндраСкачать

ЦИЛИНДР геометрия егэ по математике профильный уровень ЯщенкоСкачать

№538. Площадь боковой поверхности цилиндра равна 5. Найдите площадь осевогоСкачать

ЕГЭ БАЗА 16 номер Радиус основания цилиндра равен 15, а его образующая равна 14Скачать

Объем цилиндраСкачать

№532. Через образующую АА1 цилиндра проведены две секущие плоскости, одна из которыхСкачать

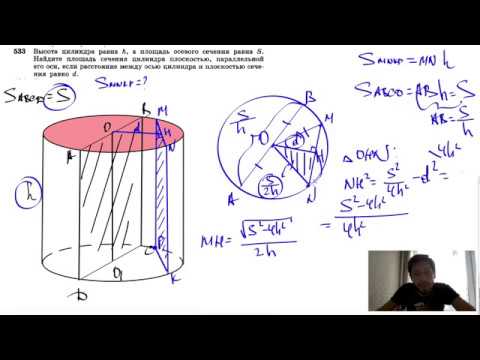
№533. Высота цилиндра равна h, а площадь осевого сечения равна 5. Найдите площадь сеченияСкачать