На вал 1 ворота намотана веревка, удерживающая груз Q (рис. 164). Радиус колеса 2 ворота в четыре раза больше радиуса вала. Веревка, прикрепленная к ободу колеса и натягиваемая грузом силой Р=80 н, сходит с колеса в точке F по касательной; радиус DF колеса образует с вертикалью угол α=60°. Определить величину груза Q, при котором ворот остается в равновесии, а также реакции подшипников A и В, если общий вес вала и колеса G=600 н и приложен в точке С (AC=0,4 м).
Видео:Термех. Статика. Решение задач на равновесие пространственной системы телСкачать

Решение задачи
1. Три нагрузки – вес G и грузы Q и Р, приложенные к вороту, уравновешиваются реакциями подшипников А и В. Нагрузки действуют в плоскостях, перпендикулярных к оси вала, и, следовательно, не смещают вал вдоль оси, поэтому и реакции подшипников расположатся в плоскостях, перпендикулярных к этой же оси. Заменим их составляющими XA, ZA и XB, ZB (рис. 164). Следует учесть, что обычный подшипник не создает реакции, направленной вдоль оси вала. Если на вал действуют нагрузки, смещающие вал вдоль оси, то один из подшипников должен быть заменен подпятником.
2. Изобразим ворот со всеми действующими на него силами в трех проекциях (рис. 165 а, б, в) и при помощи их составим уравнения равновесия.
Так же как и в предыдущей задаче, уравнение проекций на ось у превратится в тождество вида 0=0. При составлении уравнения моментов относительно оси у нужно учитывать, что радиус колеса R в четыре раза больше радиуса вала r (R=4r).
Видео:Термех. Статика. Равновесие пространственной системы силСкачать

Случаи пространственно нагруженных валов
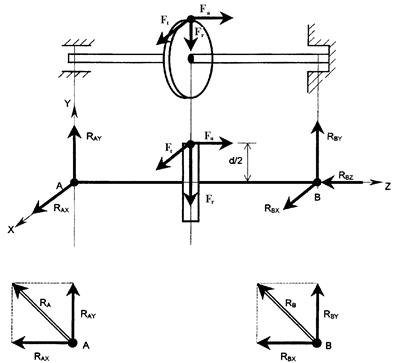
Силы в зацеплении зубчатых колес (рисунок 69):
Ft – окружное усилие, оно заставляет вращаться колесо и направлено по касательной к окружности колеса;
Fr – радиальное усилие, оно всегда направлено к центру колеса;
Fa – осевое усилие, сдвигает колесо вдоль оси вала.
Радиальные реакции подшипников:
При расчете валов необходимо составлять шесть уравнений равновесия (26). Причем, рассматривая схемы для составления уравнений моментов сил относительно осей, можно для этих схем составить также и уравнения проекций сил. В этом случае задача разбивается на три части (см. таблицу 11).
Читайте также: Размеры центровок для валов
| Уравнение равновесия | Плоскость, перпендикулярная оси, на которую проецируют силы и уравнение моментов | Дополнительные уравнения |
| Боковая плоскость XY (вид сбоку), (рассматривается, если не известны вращающие силы, например Ft): | ||
| Вертикальная плоскость YZ (вид спереди): | ||
| Горизонтальная плоскость XZ (вид сверху): |
Подумай и ответь на вопросы
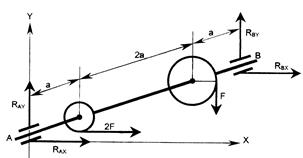
38Составить уравнение равновесия вала (рисунок 70) .
2) F·3а + RBY·4а = 0; 4) -RBY·3а – F·3а = 0.
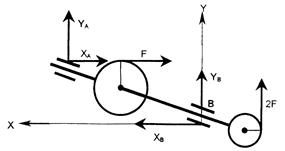
39 Составить уравнение равновесия вала (рисунок 71) .
studopedia.org — Студопедия.Орг — 2014-2021 год. Студопедия не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования (0.001 с) .
Видео:Определение опорных реакции в пространственной конструкции. ТермехСкачать

Примеры решения задач
Пример 1. На тело в форме куба с ребром а = 10 см действуют три силы (рис. 7.6). Определить моменты сил относительно осей координат, совпадающих с ребрами куба.
1. Моменты сил относительно оси Ох:
2. Моменты сил относительно оси Оу.
Пример 2. На горизонтальном валу закреплены два колеса, г1 = 0,4 м; г2 = 0,8 м. Остальные размеры — на рис. 7.7. К колесу 1 приложена сила F1, к колесу 2 — силы F2 = 12 кН, F3 = 4кН.
Определить силу F1 и реакции в шарнирах А и В в состоянии равновесия.
1. При равновесии выполняются шесть уравнений равновесия.
Уравнения моментов следует составлять относительно опор А и В.
Моменты этих сил относительно соответствующих осей равны нулю.
3. Расчет следует завершить проверкой, использовав дополнительные уравнения равновесия.
1. Определяем силу F\, составив уравнение моментов сил относительно оси Oz:
2. Определяем реакции в опоре А. На опоре действуют две составляющие реакции (YA; XA).
Составляем уравнение моментов сил относительно оси Ох’ (в опоре В).
Поворот вокруг оси Ох’ не происходит:
Знак «минус» означает, что реакция направлена в противоположную сторону.
Поворот вокруг оси Оу’ не происходит, составляем уравнение моментов сил относительно оси Оу’ (в опоре В):
3.Определяем реакции в опоре В. На опоре действуют две составляющие реакции (XB, YB). Составляем уравнение моментов сил относительно оси Ох (опора А):
Составляем уравнение моментов относительно оси Оу (опора А):
Читайте также: Ременная передача между валами
4.Проверка. Используем уравнения проекций:
Пример 3. Определить численное значение силы P1, при котором вал ВС (рис. 1.21, а) будет находиться в равновесии. При найденном значении силы Р1определить опорные реакции.
Действующие на зубчатые колеса силы Ри Р1направлены по касательным к начальным окружностям колес; силы Т и Т1 — по радиусам колес; силы А1 параллельны оси вала. Т = 0,36Р, 7Т1 = Р1; А1 = 0,12P1.
Опоры вала, изображенные на рис. 1.21, а, надо рассматривать как пространственные шарнирные опоры, препятствующие линейным перемещениям в направлениях осей и и v (выбранная система координат показана на рис. 1.21, б).
Освобождаем вал от связей и заменяем их действие реакциями VВ, НВ,VC, НС (рис. 1.21, б). Получили пространственную систему сил, для которой составляем уравнения равновесия, пользуясь выбранной системой координат (рис. 1.21,6):
где А1*1,25D/2 — момент относительно оси и силы A1, приложенной к правому зубчатому колесу.
Моменты относительно оси и сил Т1 и А1 (приложенных к среднему зубчатому колесу), Р1 (приложенной к правому зубчатому колесу) и Р равны нулю, так как силы Р, T1, Р1 параллельны оси и, а сила А1 пересекает ось и.
Составим проверочное уравнение:
следовательно, реакции VB и VС определены верно;
где А1* 1,25D/2 — момент относительно оси v силы А1, приложенной к среднему зубчатому колесу.
Моменты относительно оси v сил Т, Р1 (приложенной к среднему зубчатому колесу), А1 и Т1 (приложенных к правому зубчатому колесу) равны нулю, так как силы Т, Р1, Т1 параллельны оси v, сила А1 пересекает ось v.
Составим проверочное уравнение:
следовательно, реакции НВ и НС определены верно.
В заключение отметим, что опорные реакции получились со знаком плюс. Это указывает на то, что выбранные направления VB, НВ, VC и НС совпадают с действительными направлениями реакций связей.
Пример 4. Сила давления шатуна парового двигателя Р = 25 кН передается на середину шейки коленчатого вала в точке D под углом α = 30° к горизонту при вертикальном расположении щек колена (рис. 1.22). На конец вала насажен шкив ременной передачи. Натяжение ведущей ветви ремня в два раза больше, чем ведомой, т.е. S1 = 2S2. Сила тяжести маховика G = 10 кН.
Читайте также: Валы виды валов их нагружение
Определить натяжения ветвей ременной передачи и реакции подшипников А и В, пренебрегая массой вала.
Рассматриваем равновесие горизонтального коленчатого вала со шкивом. Прикладываем в соответствии с условием задачи заданные силы Р, S1, S2 иG. Освобождаем вал от опорных закреплений и заменяем их действие реакциями VA, НА, VB и НВ. Координатные оси выбираем так, как показано на рис. 1.22. В шарнирах А и В не возникает реакций вдоль оси w, так как натяжение ветвей ремня и все остальные силы действуют в плоскостях, перпендикулярных этой оси.
Составим уравнения равновесия:
Кроме того, по условию задачи имеем еще одно уравнение
Таким образом, здесь имеется шесть неизвестных усилий S1, S2, НА, VA, НВ иVB и шесть связывающих их уравнений.
Уравнение проекций на ось w в рассматриваемом примере обращается в тождество 0 = 0, так как все силы лежат в плоскостях, перпендикулярных оси w.
Подставляя в уравнения равновесия S1=2S2 и решая их, находим:
Значение реакции НВ получилось со знаком минус. Это значит, что в действительности ее направление противоположно принятому на рис. 1.22.
Контрольные вопросы и задания
1. Запишите формулы для расчета главного вектора пространственной системы сходящихся сил.
2. Запишите формулу для расчета главного вектора пространственной системы произвольно расположенных сил.
3. Запишите формулу для расчета главного момента пространственной системы сил.
4. Запишите систему уравнений равновесия пространственной системы сил.
5. Какое из уравнений равновесия нужно использовать для определения реакции стержня R1 (рис. 7.8)?
6. Определите главный момент системы сил (рис. 7.9). Точка приведения — начало координат. Координатные оси совпадают с ребрами куба, ребро куба равно 20 см;F1 — 20кН;F2 — 30кН.
7. Определите реакцию Хв (рис. 7.10). Вертикальная ось со шкивом нагружена двумя горизонтальными силами. Силы F1 и F2 параллельны осиОх. АО = 0,3 м; ОВ = 0,5 м; F1 = 2кН; F2 = 3,5 кН.
- Свежие записи
- Чем отличается двухтактный мотор от четырехтактного
- Сколько масла заливать в редуктор мотоблока
- Какие моторы бывают у стиральных машин
- Какие валы отсутствуют в двухвальной кпп
- Как снять стопорную шайбу с вала
🔥 Видео
Термех. Статика. Равновесие плоской произвольной системы силСкачать
Статика. 2.2. Пространственная произвольная система сил. Реакции связей прямоугольной плиты.Скачать
5.6. Равновесие произвольной пространственной системы силСкачать
Статика. Условия равновесия плоской системы сил (23)Скачать
§ 5.1. Уравнения равновесия произвольной системы силСкачать
Пространственная система сил. Часть 1Скачать
Условия равновесия систем силСкачать
Равновесие полкиСкачать
5.3. Главный момент произвольной пространственной системы силСкачать
Пространственная система силСкачать
Приведение системы сил к простейшему видуСкачать
Термех. Статика. Приведение пространственной системы сил к центруСкачать
Равновесие вала. Реакции опорСкачать
11. Произвольная пространственная система сил.(часть 1)Скачать
5.7. Равновесие системы тел под действием пространственной системы сил (1 из 2)Скачать
Статика #2Скачать
Пространственная система силСкачать