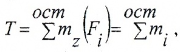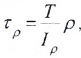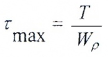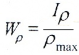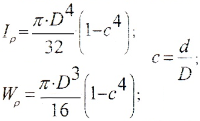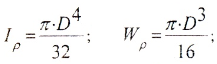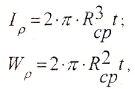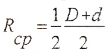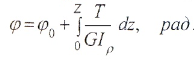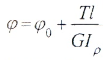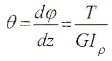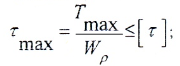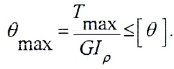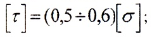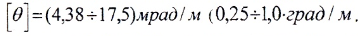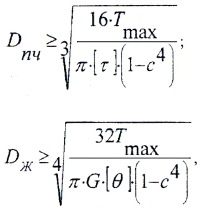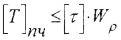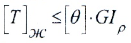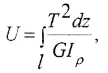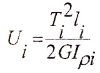Сдвиг вала при кручении (7 видео)

Кручением называется такой вид деформации бруса, при котором в его поперечных сечениях возникает только один внутренний силовой фактор – крутящий момент T.

Брусья, испытывающие кручение, принято называть валами.

Содержание

Внутренний крутящий момент
Напряжения при кручении
Деформации
Деформация кручения
Основные понятия
Напряжения кручения
🎥 Видео

Видео:Кручение. Часть 6 Жесткость валаСкачать

Внутренний крутящий момент

Внутренние скручивающие моменты появляются под действием внешних крутящих моментов m_i, расположенных в плоскостях, перпендикулярных к продольной оси бруса.

Скручивающие моменты передаются на вал в местах посадки зубчатых колес, шкивов ременных передач и т.п.

Величина крутящего момента в любом сечении вала определяется методом сечений:

т.е. крутящий момент численно равен алгебраической сумме скручивающих моментов m_i, расположенных по одну сторону от рассматриваемого сечения.

Правило знаков внутренних скручивающих моментов:
Положительными принимаются внутренние моменты, стремящиеся повернуть рассматриваемую часть вала против хода часовой стрелки, при рассмотрении со стороны отброшенной части вала.

В технике наиболее широко используются валы круглого поперечного сечения.

Теория кручения круглых валов основана на следующих гипотезах:

поперечное сечение, плоское до деформации вала, остается плоским и после деформации;
радиусы, проведенные мысленно в любом поперечном сечении, в процессе деформации вала не искривляются.

Видео:КРУЧЕНИЕ ВАЛА. Касательные напряжения. Сопромат.Скачать

Напряжения при кручении

В поперечных сечениях вала при кручении имеют место только касательные напряжения.
Касательные напряжения, направленные перпендикулярно к радиусам, для произвольной точки, отстоящей на расстоянии ρ от центра, вычисляются по формуле:

где I_ρ — полярный момент инерции.
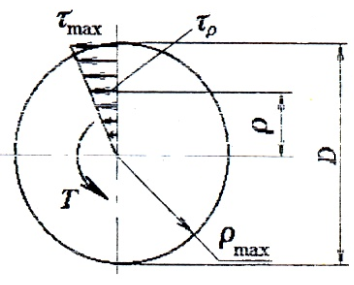
Эпюра касательных напряжений при кручении имеет следующий вид:

Касательные напряжения меняются по линейному закону и достигают максимального значения на контуре сечения при ρ= ρ_max:

Здесь:

— полярный момент сопротивления.
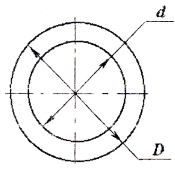
Геометрические характеристики сечений:
а) для полого вала:

б) для вала сплошного сечения (c=0)

в) для тонкостенной трубы (t 0,9)

где

— радиус срединной поверхности трубы.

Видео:Правило знаков при крученииСкачать

Деформации

Деформации валов при кручении заключаются в повороте одного сечения относительно другого.

Угол закручивания вала на длине Z определяется по формуле:

Если крутящий момент и величина GI_ρ, называемая жесткостью поперечного сечения при кручении, постоянны, для участка вала длиной l имеем:

Угол закручивания, приходящийся на единицу длины, называют относительным углом закручивания:

Расчет валов сводится к одновременному выполнению двух условий:

условию прочности:
условию жесткости:

Для стальных валов принимается:

допускаемое касательное напряжение
допускаемый относительный угол закручивания

Используя условия прочности и жесткости, как и при растяжении – сжатии можно решать три типа задач:

проверочный расчет, заключающийся в проверке выполнения условий прочности и жесткости при известных значениях крутящего момента, размеров и материала вала.
Проектировочный расчет, при котором вычисляются диаметры:

при этом берется большее из найденных значений, а затем принимается стандартное значение по ГОСТ.
Определение грузоподъемности вала:
- из условия прочности
- из условия жесткости

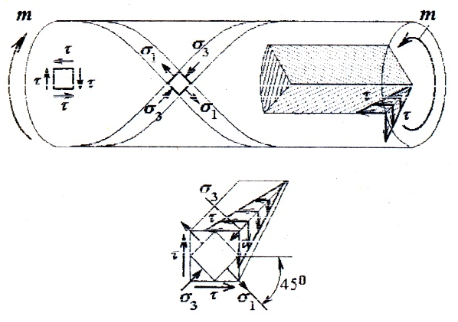
При кручении, наряду с касательными напряжениями в поперечных сечениях, в соответствии с законом парности, касательные напряжения возникают и в продольных сечениях. Таким образом, во всех точках вала имеет место чистый сдвиг.

Главные напряжения σ₁ = τ, σ₃ = -τ наклонены под углом α=±45 о к образующей.

Потенциальная энергия упругой деформации определяется по формуле

или для участка вала при постоянном T и GI_ρ

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Видео:Кручение валаСкачать

Деформация кручения

В различных механизмах детали подвергаются влиянию разных сил, приводящих к возникновению деформаций. Далее рассмотрена деформация кручения: факторы и закономерности ее проявления, формирующие ее силы, особенности деформации изделий различной формы.

Видео:11. Кручение ( практический курс по сопромату )Скачать

Основные понятия

Под кручением понимают вид деформации, свойственный для условий приложения к телу силы в поперечной плоскости. В результате этого в поперечном разрезе формируется крутящий момент. Деформациям кручения подвергаются валы и пружины.

Валом называют функционирующую на кручение вращающуюся деталь в виде стержня.

Под торсионом понимают функционирующий на кручение стержень, применяемый в качестве упругого элемента.

Для круглых валов, наиболее обширно применяемых в технике, разработана теория кручения. Она основана на трех положениях:

После деформации сохраняется плоское поперечное сечение детали.
При деформации радиусы, проходящие поперек детали, не искривляются и проворачиваются на равный угол.
При деформации продольные волокна сохраняют размеры, следовательно, разделяющие поперечные сечения расстояния неизменны.

Из приведенных положений следует, что кручение представлено деформацией сдвига материала между соседними поперечными сечениями, обусловленной проворотом последних вокруг оси.

Деформациями при кручении считают взаимный проворот сечений. Они формируются вследствие воздействия на стержень пар сил с перпендикулярными к его продольной оси плоскостями действия.

Величина деформаций описывается углом закручивания. Под полным понимают угол поворота свободного конца. Относительным считают значение для определенной длины вала. Данные параметры рассчитывают с учетом прочности и жесткости деталей.

Угол закручивания стержня цилиндрической конфигурации в границах упругих деформаций определяется уравнением закона Гука для кручения, представляющего отношение произведения момента и длины вала к произведению геометрического полярного инерционного момента и модуля сдвига.

Относительный угол закручивания вычисляют как частное угла закручивания и длины стержня.

Под вращающими либо скручивающими моментами понимают показатели пар сил, воздействующих на вал. Их подразделяют на внешние, называемые вращающими и скручивающими, и внутренние (крутящие). Под влиянием перпендикулярных продольной оси бруса внешних крутящих моментов формируются внутренние. Они передаются на деталь в точках установки шкивов ременных передач, зубчатых колес и т. д.

Крутящий момент представлен силовым фактором, обуславливающим круговое передвижение сечения относительно перпендикулярной ему оси или препятствующим ему. Его значение равно сумме скручивающих усилий по одну сторону от данной точки. Положительными считают внутренние моменты, направленные против часовой стрелки со стороны внешней нормали (отброшенной части). При этом соответствующий внешний момент имеет направление, совпадающее с ходом часовой стрелки.

Условия прочности и жесткости применяют для решения следующих задач:

Выполнения проверочного расчета данных условий для конкретных значений крутящего момента и валов определенного размера и материала.
Выполнения проектировочного расчета для вычисления диаметров и нахождения большего из них.
Определения грузоподъемности вала путем вычисления крутящего момента из обоих условий и нахождения меньшего из них.

Под эпюрой крутящих моментов понимают график, отображающий закон их изменения по длине либо сечению детали.

При разделении детали по длине на три участка в соответствии с методом сечений получится, что для первого (правого) фрагмента наблюдается линейная зависимость крутящего момента от координаты сечения ввиду влияния равномерно распределенной нагрузки, для второго и третьего участков данная зависимость отсутствует. При этом в точках приложения внешних сосредоточенных усилий наблюдаются скачки, соответствующие их величине.

В сечении наблюдается линейное изменение, определяемое законом касательных напряжений, в прямой зависимости от расстояния от центра.

Таким образом, в продольном разрезе наибольшие деформации кручения характерны для точки, наиболее удаленной от места закрепления детали. В поперечном разрезе максимальные деформации кручения наблюдаются на поверхности.

Полярный инерционный момент сечения представляет собой геометрическую характеристику жесткости при кручении для круглого вала. Полярный момент сопротивления сечения является аналогичным параметром для его прочности.

Следует отметить, что большинство приведенных выше понятий описывается с применением формул.

Видео:Кручение. Часть 5 Условие прочностиСкачать

Напряжения кручения

Исходя из приведенного выше определения деформации кручения, при данном процессе в поперечном сечении наблюдаются лишь касательные напряжения, направленные перпендикулярно к радиусам. Их определяют для конкретной точки как произведение соотношения крутящего момента к геометрическому полярному инерционному моменту и расстояния данной точки от оси кручения.

Изменение касательных напряжения линейно, и максимальной величины они достигают на поверхности при наибольших значениях крутящего момента и расстояния от оси кручения, поэтому ее значение вычисляют как частное наибольшего крутящего и полярного моментов сопротивления.

С применением данного условия возможно вычислить прочие параметры: по силовым факторам, создающим крутящий момент – показатель сопротивления и далее размеры сечения в зависимости от формы, либо по размеру сечения – максимально допустимое для него значение крутящего момента и на основе последней допустимые значения внешних нагрузок.

Касательные напряжения, по закону парности, формируются при кручении как в поперечных, так и в продольном направлениях. Вследствие этого во всех точках вала наблюдается деформация в виде чистого сдвига. Главные напряжения направлены к образующей под углом 45°.

Помимо скручивающих усилий возможно воздействие на вал моментной нагрузки.

Из изложенных выше данных следует, что удаление материала в районе оси вала незначительно сказывается на прочности ввиду того, что данная часть мало нагружена. При равных площади сечения и массе деталей кольцевые варианты характеризуются большими полярными моментами сопротивления и инерции по сравнению со сплошными валами. То есть при равной массе полые варианты прочнее и жестче, а при одинаковых показателях прочности и жесткости легче. Названные параметры определяют устойчивость данных изделий к деформации.

Выше были рассмотрены особенности деформации кручения круглых в поперечном разрезе предметов. Для треугольных, прямоугольных, эллиптических и прочих вариантов не применима гипотеза плоских сечений. Это обусловлено тем, что поверхности данного типа при кручении искривляются. Данный процесс их коробления вследствие смещения отдельных точек при деформации вдоль оси называют депланацией. Вследствие этого методы сопротивления материалов для вычисления кручений и напряжений неприменимы. Вместо них используют методы теории упругости.

Для изделий произвольной поперечной формы касательные напряжения имеют направление по касательной к контуру, однако при наличии внешних углов они отсутствуют. Так, при разложении напряжения вблизи угла по нормалям к его сторонам надвое из закона парности следует формирование касательных напряжений на свободной поверхности. Однако в данном случае она свободна от нагрузки, поэтому у внешнего угла касательные напряжения обнуляются.

Для наиболее распространенных среди вариантов некруглого сечения прямоугольных валов наибольшие напряжения характерны для поверхностных участков в середине длинных сторон. Следовательно, там наблюдается наибольшая деформация кручения.

Прямоугольные детали в сравнении с круглым характеризуются значительно меньшими жесткостью и прочностью. Причем это отличие увеличивается с ростом отношения сторон. Следовательно, они более подвержены деформации.

источники:

https://evakuatorinfo.ru/sdvig-vala-pri-kruchenii