Сила трения при вращении вала

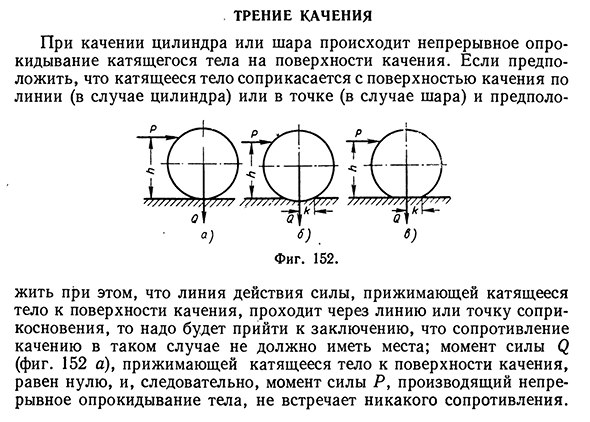
поверхности качения, равен нулю, и, следовательно, момент силы Р, производящий непре­рывное опрокидывание тела, не встречает никакого сопротивления.142 Трение в кинематических парах Между тем опыт показывает, что сопротивление качению имеет место. Сопротивление качению возникает потому, что тела, прижимаемые одно к другому некоторой, хотя бы и незначительной силой, деформируются и в деформированном состоянии соприкасаются не по линии или в точке,

а по некоторой поверхности, примыкающей к линии или точке. При деформации поверхности под катящимся Людмила Фирмаль

телом (фиг. 152, б) и при деформации катящегося тела (фиг. 152, в), а следовательно, при деформации и тела и поверхности одновременно линия или точка, около которой происходит опрокидывание, отхо­дит на некоторое расстояние k от линии действия силы Q. Вследствие этого создается плечо k силы Q и момент Qk, противодействующий опрокидывающему моменту Ph. При качении с постоянной скоростью должно иметь место оче­видное соотношение Ph = Qk, где k — величина, характеризующая условия, при которых проис­ходит качение; она называется к о э ф ф и ц и е н т о м т р е н и я к а ч е н и я. В отличие от коэффициента трения скольжения коэф­фициент трения качения является величиной с линейной размер­ностью. Явление качения наблюдается благодаря наличию трения сколь­жения:

качение одного тела по другому может происходить только в том случае, если сопротивление скольжению превышает сопро­тивление качению. Для того, чтобы заставить тело катиться по плоскости, надо при­ложить к телу силу, равную а для скольжения необходимо приложить силу, равную Pc = Qf-Если и, следовательно, Рк Людмила Фирмаль

парах общий вес колес и 2) момент силы трения скольжения frQ, где г — радиус осей колес. Поэтому получаем p ^ = = (Q + G )& +/rQ , откуда п _ (Q + G) & + frQ. г

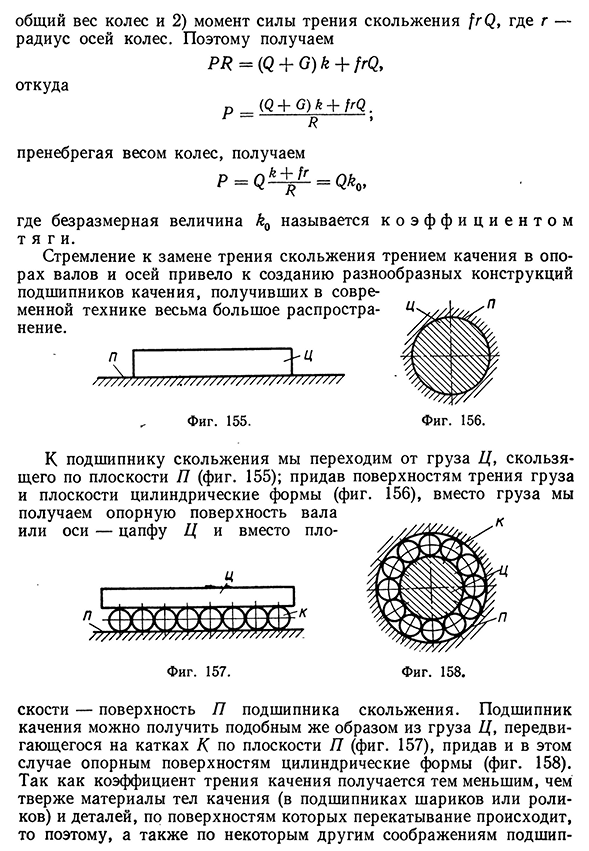
Я пренебрегая весом колес, получаем P = Q ^ = Qo> где безразмерная величина kQ называется к о э ф ф и ц и е н т о м т я г и. Стремление к замене трения скольжения трением качения в опо­рах валов и осей привело к созданию разнообразных конструкций подшипников качения, получивших в совре­менной технике весьма большое распростра­нение. Фиг. 155. Фиг. 156. К подшипнику скольжения мы переходим от груза Ц, скользя­щего по плоскости П (фиг. 155); придав поверхностям трения груза и плоскости цилиндрические формы (фиг. 156), вместо груза мы получаем

опорную поверхность вала или оси — цапфу Ц и вместо плоФиг. 158. скости — поверхность П подшипника скольжения. Подшипник качения можно получить подобным же образом из груза Ц, передви­гающегося на катках Д по плоскости П (фиг. 157), придав и в этом случае опорным поверхностям цилиндрические формы (фиг. 158). Так как коэффициент трения качения получается тем меньшим, чем тверже материалы тел качения (в подшипниках шариков или роли­ков) и деталей, по поверхностям которых перекатывание происходит, то поэтому, а также по некоторым другим соображениям подшип-Трение качения 145 ники качения изготовляются из твердых материалов в виде двух колец с шариками или роликами между ними. Для того чтобы рас­стояния между телами качения при

перекатывании их по поверхно­стям колец оставались неизменными, в современных подшипниках тела качения отделяются одно от другого при помощи особых деталей, называемых сепараторами. В СССР подшипники качения изготовляются на больших механи­зированных заводах и являются объектами массового производства. Многочисленные типы, конструкции и размеры подшипников качения стандартизованы. На фиг. 159 приведена одна из стандартных конструкций ради­ального подшипника, т. е. подшипника, предназначенного для вос­приятия усилий в радиальном направлении; такие подшипники могут воспринимать усилия и в осевом направлении, приблизи­тельно в 1,5 раза меньше радиальных. На фиг. 160 приведена одна из стандартных конструкций упорного

Читайте также: Компрессор от мастер кит для чего он

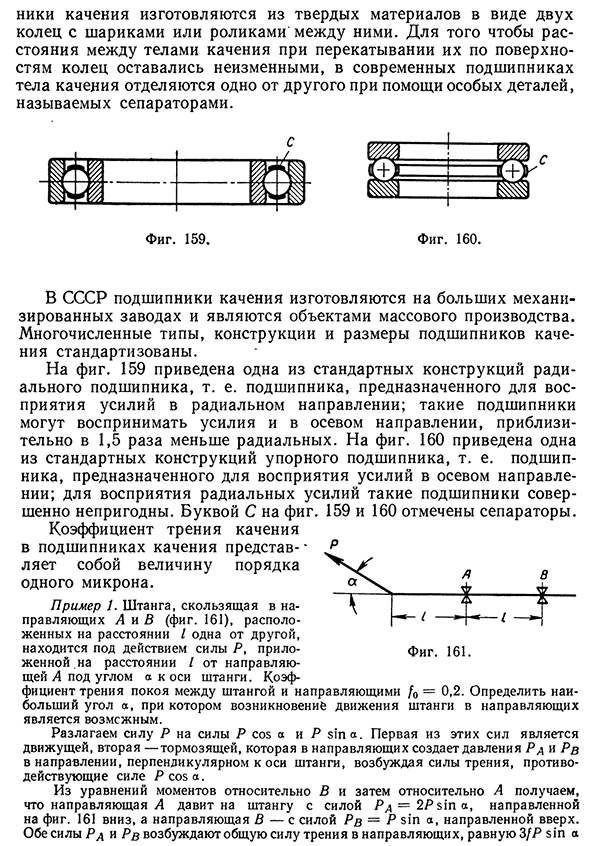
подшипника, т. е. подшип­ника, предназначенного для восприятия усилий в осевом направле­нии; для восприятия радиальных усилий такие подшипники совер­шенно непригодны. Буквой С на фиг. 159 и 160 отмечены сепараторы. Коэффициент трения качения в подшипниках качения представ ляет собой величину порядка одного микрона. Пример 1. Штанга, скользящая в на­правляющих А и В (фиг. 161), располо­женных на расстоянии / одна от другой, находится под действием силы Р, прило­женной. на расстоянии I от направляю­щей А под углом а к оси штанги. Коэф­фициент трения покоя между штангой и направляющими /0 = 0,2. Определить наи­больший угол а, при котором возникновение движения штанги в направляющих является возможным. Разлагаем силу Р на силы Р cos а и Р sin а. Первая из этих сил является движущей, вторая —тормозящей, которая в направляющих создает давления Рд и Рв в направлении, перпендикулярном к оси штанги, возбуждая силы трения,

Видео:Сила тренияСкачать

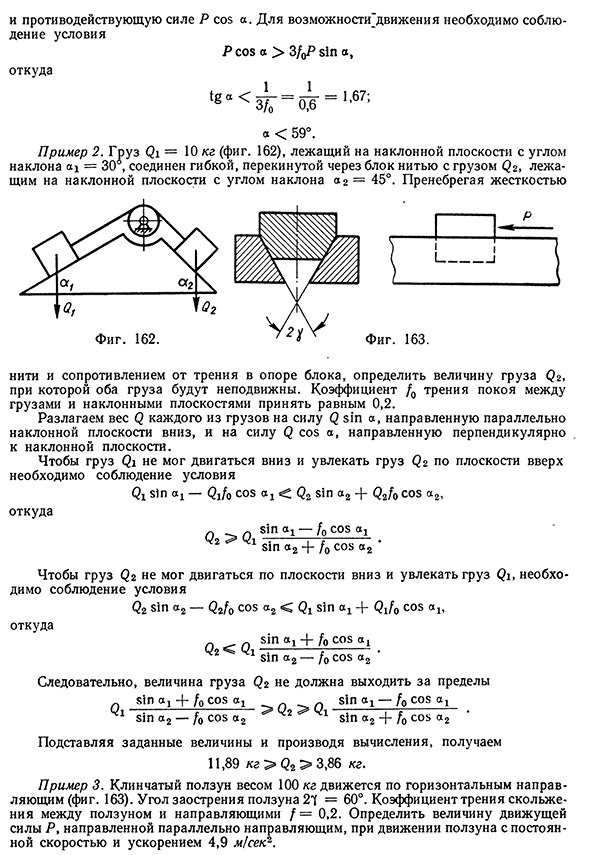
противодействующие силе P c o sa. Из уравнений моментов относительно В и затем относительно А получаем, что направляющая А давит на штангу с силой Рд = 2Psin а, направленной на фиг. 161 вниз, а направляющая В — с силой Рв = Р sin а, направленной вверх. Обе силы Рд и Рв возбуждают общую силу трения в направляющих, равную 3fP sin a 10 Зиновьев 612146 Трение в кинематических парах и противодействующую силе Р cos а. Для возможности’движения необходимо соблю­дение условия Р cos а > 3/qP sin а, откуда а Q i S i n a i T V ° S a i • Sin a2 + 7o COS a2 Чтобы груз Q2 не мог двигаться по плоскости вниз и увлекать груз Qi, необхо­димо соблюдение условия Q2 sin a2 — Q2/0 cos a2 Q sin ax — fo cos a, Q2 > 3,86 кг. Пример 3. Клинчатый ползун весом 100 кг движется по горизонтальным направ­ляющим (фиг. 163). Угол заострения ползун

а 27 = 60°. Коэффициент трения скольже­ния между ползуном и направляющими f — 0,2. Определить величину движущей силы Р, направленной параллельно направляющим, при движении ползуна с постоян­ной скоростью и ускорением 4,9 м/сек2.Примеры 147 Фиктивный коэффициент трения f f sin i sin 30 ° = 2/ = 0,4. Сила трения F = 100 кг-0,4 = 40 кг. Сила, необходимая для поддержания постоянной скорости движения, Р = F = 40 кг. Масса ползуна 1 0 0 2/ т — кг-сек^/м. У, о Сила, необходимая для движения ползуна с ускорением 4,9 м/сек?, Р = F + 4,9т = 40 + 4,9 т-з= 90 кг. 9,о Пример 4. Ведущее фрикционное колесо с диаметром Di = 300 мм (фиг. 164) и числом оборотов в минуту Л1 — 300 передает мощность N = 4 л. с. ведомому колесу с диаметром D 2 = = 450 мм. Коэффициент трения в месте соприкосновения ободов

колес f — 0,2. Валы, на которых наса­жены колеса, вращаются в подшипни­ках с диаметрами 40 мм. Коэффициент трения в опорах валов /1 = 0,08. Определить потери мощности от трения в опорах валов при колесах с цилин­дрическими ободами и колесах с клин­чатыми ободами. Угол заострения клинчатого обода 21 = 30° (фиг. 165). Угловая скорость вращения Фиг. 165. ведущего колеса При мощности N = 4 л. с. — 4-75 кем! сек = ЗШкгм/сек момент на валу ведущего колеса М — 300 кем)сек: 31,4 сек1 = 9,55 кем. Окружное усилие Р — 9,55 кем: М = 63,7 & 64 кг. Сила, с которой колеса должны быть прижаты одно к другому при цилиндри-ческих ободах, 10148 Трение в

кинематических парах Сила S, воспринимаемая опорами каждого из валов, является геометрической суммой двух слагающих: окружного усилия и силы Q. Так как линии действия этих £ил перпендикулярны одна к другой, то S = У/>2 +

Трение во вращательной кинематической паре

Рассмотрим вращательную кинематическую пару в наиболее часто встречающемся случае, когда сопряжение вала с отверстием осуществляется с зазором (рис. 5.11). На указанном рисунке зазор между валом и отверстием весьма преувеличен для того, чтобы лучше видеть элементы сопряжения. Вал нагружен поперечной силой , которая является известной величиной. При отсутствии вращения окружность вала касается окружности отверстия в точке на его вертикальном диаметре. Когда вал вращается в направлении , то, в результате действия силы трения , он «взбирается» на стенку вала и в равновесном состоянии устанавливается, касаясь окружности отверстия в точке . При этом реакция стенки отверстия равна и противоположна силе . Нормальная реакция направлена вдоль нормали в точке касания окружностей, то есть вдоль линии, проходящей через точку касания и их центры. Сила трения направлена по касательной к окружностям, проходящей также через точку касания , навстречу окружной скорости вала. Радиус цапфы вала обозначен r (цапфой называется участок вала, который находится внутри отверстия опоры).

Читайте также: Какие трамваи ходят до госпитального вала

Сопротивление вращению вала создаётся моментом трения , равным произведению силы трения на радиус цапфы, то есть . Сила трения, как известно, определяется формулой . Из силового треугольника по теореме Пифагора имеем , или , откуда . Поэтому сила трения , а момент трения . Так как коэффициент трения , то , тогда (например, , , а ). Поэтому можно принять, что . Произведение радиуса цапфы на коэффициент трения является для данных условий постоянной величиной, определяемой только геометрией вала и условиями трения. Эта величина измеряется в линейных единицах, обозначается и называется кругом трения, который описывается этим радиусом при вращении вала (круг трения на рис. 5.11 заштрихован). Так что радиус круга трения . Таким образом, при известном момент трения вычисляется по формуле .

Значение круга трения заключается в том, что полная реакция во вращательной паре проходит по касательной к нему, никогда не пересекая его. При этом её направление таково, что момент реакции относительно центра вала направлен против скорости вращения вала.

Видео:Урок 39 (осн). Сила трения. Коэффициент тренияСкачать

Р а с ч ё т п о т е р ь м о щ н о с т и н а т р е н и е в о в р а щ а т е л ь -н о й п а р е. Реакции в кинематических парах, вычисляемые с помощью методов планов сил и других методов, являются, по существу, нормальными реакциями, так как они определялись в предположении отсутствия трения. Это значит, что коэффициент трения предполагался равным нулю, и, соответственно угол трения также принимался равным нулю. Поэтому для определения мощности трения необходимо знать момент силы трения и относительную угловую скорость одного звена пары по отношению к другому, то есть . Представим на рис. 5.12 вращательную пару, образованную звеньями 1 и 2, с увеличенным изображением её элементов. Предположим, что касание элементов пары происходит в точке A. В этой точке действуют реакции со стороны первого звена на второе и со стороны второго звена на первое. В этой же точке приложена сила трения , препятствующая движению второго звена относительно первого. Сила трения определяется формулой (здесь и далее имеется в виду, что рассматривается движение второго звена относительно первого, а не наоборот). Из рисунка видно, что момент трения может быть определён как , где d – диаметр цапфы вала. Относительная угловая скорость определяется с помощью метода обращения движения: если обоим звеньям пары сообщить движение с угловой скоростью, равной и противоположно направленной угловой скорости звена 1, то это звено остановится, а второе будет вокруг него вращаться с угловой скоростью , которая и будет относительной скоростью звена 2 относительно звена 1. Таким образом, мощность трения, равная , окончательно выразится формулой

Трение качения

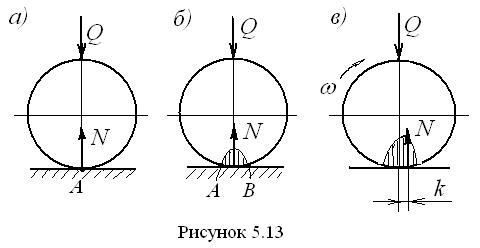
Как было указано выше, трение качения относится к трению II рода и является характерным для высших кинематических пар. Происхождение сопротивления при качении можно объяснить следующим образом. Предположим, имеется каток (цилиндр) на плоскости (рис. 5.13). Если и цилиндр, и плоскость – абсолютно твёрдые тела, то в их контакте нет никаких деформаций, и они касаются друг друга в точке A. При этом, если на каток действует вертикальная сила Q (рис. 5. 13, а), то она вызывает появление реакции плоскости, которая равна и противоположна силе Q, то есть .

Читайте также: Шпонку из приводного вала

Реакция плоскости приложена точно в точке A её касания с цилиндром. Однако, в связи с тем, что абсолютно твёрдые тела в природе не существуют, в месте касания цилиндра и плоскости образуется площадка смятия A–B, на которой, согласно Г. Герцу, при неподвижном цилиндре давление распределяется по закону эллипса (рис. 5.13, б). Равнодействующая сил этого распределения проходит точно по вертикальному диаметру цилиндра и уравновешивает силу Q. Если цилиндр катится по плоскости, то распределение сил в контакте перестаёт быть эллиптическим (рис. 5.13, в), и равнодействующая этого распределения смещается с вертикального диаметра навстречу окружной скорости цилиндра, создавая относительно его центра момент на плече . Этот момент и препятствует качению цилиндра. Смещение равнодействующей вызвано наличием упругого гистерезиса в материале цилиндра и плоскости, причиной которого является внутреннее трение в материале. В результате перед катящимся цилиндром возникает подпорная волна (редан), которая и смещает результирующую реакцию.

Расстояние , на которое смещается реакция N, называется коэффициентом трения качения. Он измеряется в сантиметрах (см). Приведём в качестве примера несколько значений коэффициентов трения качения для различных сочетаний материалов:

Ролики или шарики из закалённой стали по стали….0,0005 – 0,0010

У с л о в и я п е р е х о д а т р е н и я к а ч е н и я в т р е н и е с к о л ь- ж е н и я. Из практики известно, что если к цилиндру, находящемуся на плоскости, приложить силу достаточно высоко от плоскости, то цилиндр будет катиться. Если силу приложить очень низко, то цилиндр будет скользить по плоскости, но не катиться. Выясним, при каких условиях возможно качение, и при каких – скольжение. Для этого обратимся к рис. 5.14. На нём показан цилиндр на плоскости, на который действует сверху вниз сила Q, нормальная реакция плоскости N, равная силе Q, сила трения со стороны плоскости и, наконец, сила P, перемещающая цилиндр по плоскости. Реакция плоскости N смещена вправо от вертикального диаметра цилиндра на величину коэффициента трения качения k. Условие качения цилиндра можно определить так: , скольжение требует обратного неравенства: . Сила трения . Составим уравнение равновесия цилиндра в форме моментов: . Из этого уравнения получаем . Тогда условие качения получится как , или . Так как и являются величинами постоянными, а изменить можно только , то условие качения целесообразно записать в виде . Обратное неравенство соответствует условию скольжения: .

Видео:Момент инерцииСкачать

Потери мощности на трение качения определяются произведением момента трения качения на угловую скорость качения, то есть . Момент трения качения равен произведению , или , поэтому окончательно .

Вопросы для самопроверки

1. Назовите виды трения, характерные для низших, высших кинематических пар.

2. Как объяснить наличие трения скольжения?

3. Каким закономерностям подчиняется трение скольжения?

4. Как вычисляется сила трения скольжения?

5. Что такое коэффициент трения? От чего зависит величина коэффициента трения?

6. Что такое угол трения, конус трения?

7. Какую роль играют угол и конус трения в поступательной паре?

8. При каком условии движущая сила не может осуществить движение ползуна по плоскости?

Видео:Физика 7 класс (Урок№16 - Сила трения. Трение в природе и технике.)Скачать

9. В каком случае наклонная плоскость является самотормозящейся?

11. Что такое коэффициент потерь?

12. Что такое приведённый коэффициент трения клинчатого ползуна?

13. Как определяется мощность трения в поступательной паре?

14. Как определяется КПД винтовой пары?

15. Что такое круг трения во вращательной паре?

16. В чём значение круга трения во вращательной паре?

17. В чём существо трения качения?

18. Как определить момент трения качения?

19. Как определить мощность трения качения?

Видео:Силы трения между соприкасающимися поверхностями твердых тел | Физика 10 класс #15 | ИнфоурокСкачать

20. Как определяется КПД механизма?

Динамика машин

В динамике рассматривается движение машин (или механизмов) в связи с силами, действующими на их звенья. Основными задачами этого раздела являются:

1. Определение фактической угловой скорости ведущего звена механизма.

2. Определение момента инерции маховика, необходимого для поддержания изменения угловой скорости в заданных пределах.

3. Уравновешивание и балансировка вращающихся звеньев.

4. Уравновешивание механизмов.

5. Виброзащита и виброизоляция машин и устройств.

• Свежие записи
  • Чем отличается двухтактный мотор от четырехтактного
  • Сколько масла заливать в редуктор мотоблока
  • Какие моторы бывают у стиральных машин
  • Какие валы отсутствуют в двухвальной кпп
  • Как снять стопорную шайбу с вала

  
  

  источники:

  Видео:Трение каченияСкачать

  

  https://evakuatorinfo.ru/sila-treniya-pri-vraschenii-vala

  📽️ Видео

  Сила трения. Трение покоя | Физика 7 класс #23 | ИнфоурокСкачать

  

  Определение работы силы тренияСкачать

  

  Физика 10 класс (Урок№10 - Силы трения.)Скачать

  

  Сила трения. Закон Кулона - Амонтона. 10 класс.Скачать

  

  9 класс, 20 урок, Сила тренияСкачать

  

  Сила трения покоя и сила трения скольженияСкачать

  

  Урок 44. Вращение твердого тела. Линейная и угловая скорость. Период и частота вращения.Скачать

  

  Урок 40 (осн). Трение качения. Трение в жидкостях и газахСкачать

  

  Лабораторная работа «Измерение работы силы трения»Скачать

  

  Работа силы тренияСкачать

  

  Сила трения (для чайников)Скачать

  

  Сила тренияСкачать

  

  Момент силыСкачать

  

  Физика 7 класс. §32 Сила тренияСкачать