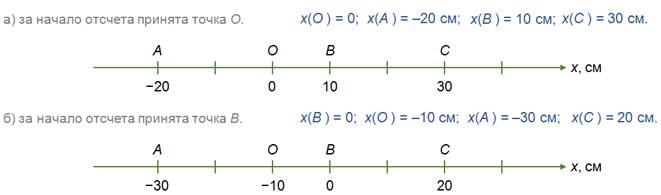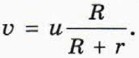Скорость движения точек цепи относительно велосипеда скорости движения точек шины

На приведённом рисунке хорошо видно, что все точки расположенные на радиусе колеса при совершении им одного оборота занимают те же самые места, на которых они были до начала вращения. Иными словами все точки радиуса колеса за один оборот перемещаются на одно и то же расстояние.

В то же время из школьного курса математики известно, что длина окружности равна:

Если прокатить колесо по поверхности и затем замерить пройденный им путь, то он будет точно соответствовать длине его окружности. Таким образом, две точки колеса: центр вращения и точка на внешней окружности проходят путь точно соответствующий приведённому расчёту. Но вот в отношении меньших радиусов мы приходим к выводу, что траектория их движения противоречит каноническому утверждению.

Так путь пройденный точкой, расположенной на половине радиуса колеса (r = R/2) должен быть равен:

C(r) = пиR, т.е. в половину меньше траектории точки расположенной на внешней окружности.

Но на самом деле она проходит фактически путь вдвое больший.

Соотношение фактически пройденной траектории и фактической дины окружности описываемый соответствующим радиусом растёт с уменьшением радиуса, фактически до бесконечности. Но в точке вращения он вновь возвращается к единице.

Самое удивительное в том, что если вырезать любую внутреннюю часть колеса и измерить его окружность, то она точно будет соответствовать вычисленной по канонической формуле.

Рассмотренный парадокс усиливается в случае, если колесо прокатывается с внешней стороны другой окружности. В этом случае траектория внутренних радиусов становится больше траектории точки на внешнем радиусе. И, наоборот, при прокатывании с внутренней стороны их траектория становится меньше.

Таким образом, можно сделать вывод о том, что траектория точек расположенных на внутренних радиусах колеса зависти не от величины собственного радиуса, а от радиуса внешней окружности. Что при этом происходит с материальными точками колеса расположенных на этих радиусах в пространстве остаётся загадкой.

Единственно разумное объяснение этого феномена предложил Галилей. Он считал, что поскольку фактическая траектория движения внутренних точек значительно больше фактической длины окружности, то точки внутренних радиусов проходят наблюдаемую траекторию с большей скоростью, чем это предписано им физикой [1]:

V = w*R, где w — угловая скорость вращения колеса.

Фактически линейная скорость внутренних точек колеса должна описываться уравнением:

V = n*w*r, где n = R/r
R – внешний радиус колеса;
r – внутренний радиус.

Иными словами линейная скорость точек внутренних радиусов является величиной постоянной и зависит только от внешнего радиуса колеса.

Вывод прямо скажем обескураживающий, но иного разумного объяснения пока ни кто не предложил.

Математически парадокс колеса в интерпретации Галилея описывается следующим уравнением:

dV = w*(R-r), где
dV – изменение скорости движения внутренних точек колеса;
R – внешний радиус колеса;
r – внутренний радиус колеса.
При r = R dV = 0
При r = 0 dV = w*R

Иными словами, изменение скорости точек расположенных на внутренних радиусах колеса меняется пропорционально от 0 на внешнем радиусе до V=w*R в центре вращения колеса. Поэтому ось колеса перемещается в пространстве с той же скоростью, которая соответствует линейной скорости вращающегося движения внешней окружности колеса при его прямолинейном движении. Соответственно такую же скорость имеют и все внутренние точки колеса.

Читайте также: Зимние шины в тихорецке

С физической точки зрения полученный результат интерпретируется как движение жёсткого стержня, расположенного перпендикулярно направлению линейного движения оси вращения. Если рассмотреть движение такого стержня без привязки его к вращательному движению, то не трудно заметить, что все материальные точки стержня имеют одну и ту же скорость.

Преобразование вращательного движения в линейно-поступательное в данном случае решается методом рычага в рамках курса теоретической механики, которой к сожалению во времена Галилея ещё не существовало.

[1] Очевидно, именно по этому, этот парадокс практически не обсуждается в научной литературе.

Поскольку один из комментаторов так возбудился после прочтения этой статьи, что внёс меня в свои чёрные списки, и у меня нет возможности ему ответить иным путём, поэтому использую материал статьи не по назначению.

Сазонов Сергей 3 сентября 2019 года в 12:54

Писать рецензию на Вашу бредятину «Парадокс колеса» считаю излишним (много чести) — найдите в детском журнале «Квант» за 1975 год статью «ЦИКЛОИДА» . Там — примерно этот круг вопросов. Парадокса нет.
(конец цитаты)

К сожалению, найти указанный журнал в Интернете не смог, поэтому не смог лично ознакомиться со статьёй. Но уже само её название «ЦИКЛОИДА» говорит о том, Сергей Сазонов не видит разницы между прямой и циклоидой. В парадоксе колеса траектория меньшего радиуса разворачивается не в виде циклоиды, а в виде прямой линии. В этом то, как раз, и заключается парадокс. С другой стороны, то, что этим парадоксом интересовались Аристотель, Галилей, и возможно другие, не менее, замечательные умы человечества, говорит о том, что парадокс действительно существовал.
Уничижительное отношение к оппонентам явный признак ограниченной умственной деятельности. Конечно, можно было и не обращать внимание на подобные выпады, но, к сожалению, подобный уровень комментаторов встречается не так уж редко, поэтому считаю необходимым противостоять банальному хамству.

Видео:Как это сделано. Трансмиссия велосипеда. Фильм Дискавери. How Do They Do It Discovery channelСкачать

Основные понятия кинематики. Относительность движения (практика)

Урок 2. Подготовка к ЕГЭ по физике. Часть 1. Механика.

Видео:Две цепи на велосипед?😳Скачать

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Основные понятия кинематики. Относительность движения (практика)»

В данной теме будет рассмотрено решение некоторых типовых задач по кинематике.

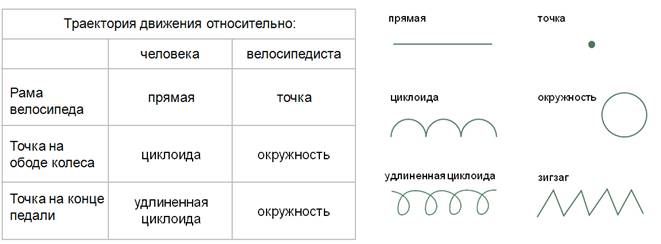
Задача 1. Велосипедист движется по прямолинейному гладкому участку дороги. Каковы траектории движения относительно велосипедиста и относительно стоящего на обочине человека рамы велосипеда; точки на ободе колеса; точки на конце педали?

Начнем с определения вида траектории рамы велосипеда. Здесь все очень просто: так как относительно велосипедиста рама неподвижна, то траекторией ее движения будет являться точка.

Читайте также: Кто носил шину шанца для новорожденных

Относительно же человека, стоящего на обочине дороги, рама будет двигаться прямолинейно, «вычерчивая» в воздухе прямую линию.

Теперь исследуем движение точки, располагающейся на ободе колеса, относительно велосипедиста. Представьте, что вы сели на велосипед, приметили положение ниппеля на переднем колесе и не спеша надавили на педаль, не выпуская ниппель из поля зрения. Какую траекторию описывает ниппель.

Точка, располагающаяся на ободе колеса, относительно велосипедиста, описывает окружность. Аналогично будет себя вести и точка, находящаяся на конце педали

Теперь разберемся с траекторией движения точки на ободе колеса, относительно человека, стоящего на обочине. Вновь обратимся к мысленному эксперименту. Мы стоим на обочине, а мимо нас проезжает велосипедист. Зафиксировали взгляд на какой-либо точке колеса (пусть это будет, например, светоотражатель на конце спицы) и проследим за ее траекторией.

Получаются кривые, которые принадлежат семейству циклоид. Значит траекторией движения точки на ободе колеса относительно неподвижного человека на обочине является циклоида.

Траекторией движения точки на конце педали относительно неподвижного человека на обочине будет являться удлиненная циклоида.

Задача 2. Можно ли принять Землю за материальную точку при расчете: а) расстояния от Земли до Солнца; б) пути, пройденного Землей по орбите вокруг Солнца за месяц; в) длины экватора и г) скорости движения Земли по орбите вокруг Солнца?

Тело можно принять за материальную точку, если:

1) тело движется поступательно;

2) размеры тела много меньше расстояния, которое оно проходит;

3) размеры тела много меньше расстояния до тела отсчета.

Рассмотрим вариант а более подробно. Для это проверим выполнение выше названных условий. Согласно первому условию, тело должно двигаться поступательно. Для этого случая оно не выполняется, так как о движении Земли в условии задачи ничего не говорится. Второе условие материальной точки также не выполняется, так как не известно расстояние, пройденное Землей. По третьему условию размеры тела должны быть намного меньше расстояния до тела отсчета. В данном случае, тело отсчета — это Солнце. Среднее расстояние от Земли до Солнца составляет 149,6 миллионов км, а средний радиус нашей планеты всего 6371 км, что, конечно же, намного меньше среднего расстояния до Солнца.

Следовательно, в первом примере Землю можно принять за материальную точку, так как выполняется третье условие.

Во втором примере Землю можно принять за МТ, т. к. ее размеры много меньше расстояния, которое она проходит по орбите за месяц.

В примере «в» Землю нельзя считать МТ, т. к. при расчете длины экватора Земли нельзя пренебречь ее размерами.

В последнем примере Землю можно считать МТ, т. к. размеры Земли (радиус 6371 км) во много раз меньше расстояния до Солнца (149,6 млн. км).

Задача 3. На рисунке указаны положения точек А, О, В, С и направление оси Х. Перерисуйте рисунок и определите координаты точек, если: а) за начало отсчета принята точка О; б) за начало отсчета принята точка В.

Читайте также: Как узнать дату производства шин йокогама

Задача 4. Мяч вертикально упал с высоты 3 м, отскочил от пола и был пойман на высоте 1 м. Сделайте чертеж. Найдите путь и модуль перемещения мяча.

«Упражнение, друзья, даёт больше,

Видео:ЧТО ТАКОЕ ЧЕЙНЛАЙН?Скачать

Катящееся колесо

Рассмотрим движение различных точек колеса автомобиля.

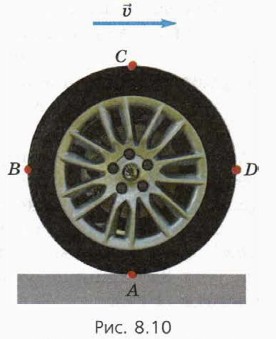
Пусть автомобиль едет со скоростью (рис. 8.10), причём его колёса катятся без проскальзывания.

Что означают слова «без проскальзывания»? Это значит, что нижняя точка колеса А покоится относительно земли (при этом шины оставляют чёткие следы). Этот факт — отправная точка для нахождения скорости всех других точек колеса — например, точек В, С, D на рисунке 8.10.

Чтобы найти скорость этих точек, удобно перейти в систему отсчёта, связанную с автомобилем, а потом вернуться в систему отсчёта, связанную с дорогой.

В системе отсчёта, связанной с автомобилем, все точки обода колеса движутся по окружности с равными по модулю скоростями. Обозначим υ_вр модуль этой скорости, обусловленной вращением колеса вокруг своей оси. Выясним: как связаны скорость автомобиля и и скорость вращения υ_вр точек его колеса? Именно тут нам и поможет тот факт, что нижняя точка колеса А покоится относительно земли.

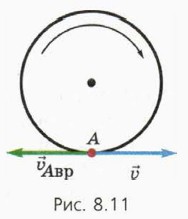
Заметим, что скорость _Авр вращения нижней точки А направлена противоположно скорости автомобиля (рис. 8.11).

_А = _Авр + .

Итак, скорости _Авр и направлены противоположно, а их сумма _А = 0. Следовательно,

то есть скорость движения точек обода колеса в системе отсчёта, связанной с автомобилем, равна по модулю скорости автомобиля.

15. Докажите, что скорость точки С (см. рис. 8.10) относительно дороги равна 2υ.

16. Найдите направление и модуль скорости точек В и D (см. рис. 8.10) относительно земли.

17. Катушка с ниткой (рис. 8.12) может катиться по горизонтальному столу без проскальзывания. Конец нити тянут в горизонтальном направлении со скоростью, равной по модулю u (рис. 8.13). Внутренний радиус катушки r, а внешний R. Докажите, что катушка будет двигаться вправо со скоростью

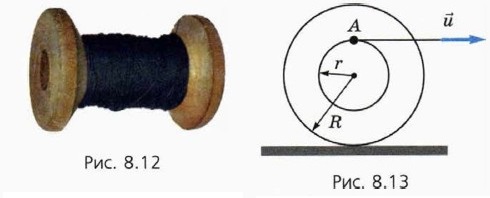
П о д с к а з к а. Рассмотрите движение точки А, воспользовавшись сложением скоростей, а также тем фактом, что точка катушки, касающаяся стола, покоится относительно стола.

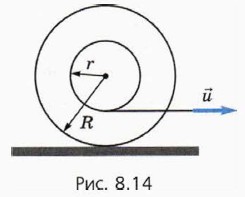
18. С какой скоростью υ и в каком направлении будет двигаться катушка в случае, изображённом на рисунке 8.14?

Если вы выполнили это задание правильно, ответ может показаться вам неправдоподобным. Попробуйте проверить его на опыте, проследив за тем, чтобы катушка катилась без проскальзывания.

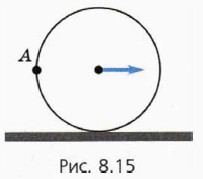
19. С какой скоростью едет велосипедист, если сорвавшаяся с колеса в точке А (рис. 8.15) капелька попала снова в эту же точку? Радиус колеса 30 см.

П о д с к а з к а. Перейдите в систему отсчёта, связанную с велосипедистом.

• Свежие записи
  • Нужно ли менять пружины при замене амортизаторов
  • Скрипят амортизаторы на машине что делать
  • Из чего состоит стойка амортизатора передняя
  • Чем стянуть пружину амортизатора без стяжек
  • Для чего нужны амортизаторы в автомобиле

  🔍 Видео

  Ремень vs ЦепьСкачать

  

  Какая мощность? #электровелосипед #diy #surronСкачать

  

  Складной велосипед SKILL BIKE 3052Скачать

  

  Тест на скорость после снятия ограничения Колхозник SV16 48В-500ВтСкачать

  

  Эксплуатация привода в три цепиСкачать

  

  Как размер звезд влияет на износ и эффективность?!Скачать

  

  Как определить оптимальную длину цепи велосипеда.Скачать

  

  Ремённая передача на велосипеде | Преимущества и недостаткиСкачать

  

  CeramicSpeed Driven 99 | Революционная трансмиссия будущего - подробно!Скачать

  

  Передаточное число на велосипеде (соотношение звезд на Bmx и Singlespeed)Скачать

  

  Выжимаем 800Ватт из 350Ваттного велосипедного двигателя (Ч4: тест)Скачать

  

  Студенты российского вуза разработали вечный двигатель #вечныйдвигатель #изобретенияСкачать

  

  2 Особенности электронных скоростей в контроллере электро велосипеда.Скачать

  

  Как увеличить скорость электротранспорта , если у вас паспортная скорость 25км/ч Часть 2Скачать

  

  Schindelhauer Viktor - ГОРОДСКОЙ КАЙФ! Тест велосипеда с ремнем вместо цепи.Скачать

  

  ЛАЙФХАК Что-бы у вас не украли велосипед #shortsСкачать

  

  Как выглядит 70 кг сухой мышечной массы в футболке и без неё.Скачать