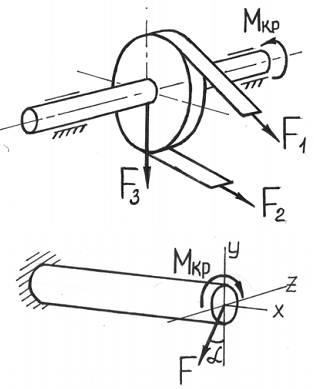
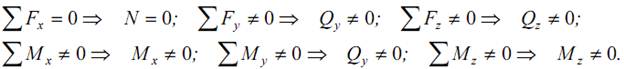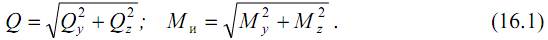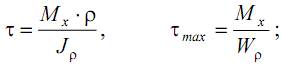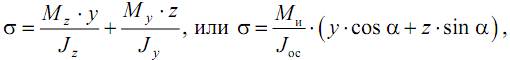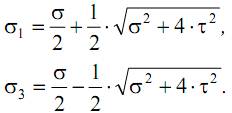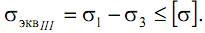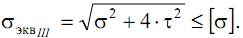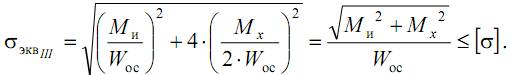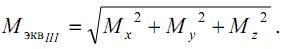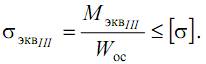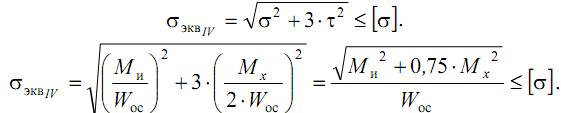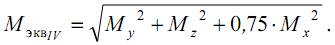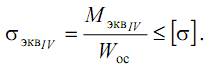Сложное сопротивление – одновременное действие на брус нескольких простых видов деформаций: растяжения-сжатия, сдвига, кручения и изгиба. Например, совместное действие растяжения и кручения.
Видео:Лекция "Сложное сопротивление" (теор. прочности, косой изгиб, внецетр. раст.-сж.,кручение с изгибом)Скачать

Косой изгиб.
Косой изгиб – это изгиб, при котором плоскость действия изгибающего момента не совпадает ни с одной из главных плоскостей инерции сечения бруса.
В общем случае при косом изгибе в поперечных сечениях возникают четыре внутренних силовых фактора: поперечные силы Qx, Qy и изгибающие моменты Mx , My. Таким образом, косой изгиб можно рассматривать как сочетание двух плоских поперечных изгибов во взаимно перпендикулярных плоскостях. Влиянием поперечных сил на прочность и жесткость бруса обычно пренебрегают.
Нейтральная линия при косом изгибе всегда проходит через центр тяжести сечения.
Условие прочности при косом изгибе:
где ymax, xmax — координаты точки сечения, наиболее удаленной от нейтральной оси.
Для сечений, имеющих две оси симметрии, максимальные напряжения будут в угловых точках, а условие прочности:
где Wx , Wy – осевые моменты сопротивления сечения относительно соответствующих осей.
Если материал бруса не одинаково работает на растяжение и на сжатие, то проверку его прочности выполняют по допускаемым и растягивающим и сжимающим напряжениям.
Прогибы при косом изгибе определяют, используя принцип независимости действия сил, геометрическим суммированием прогибов вдоль направления главных осей:
Видео:Изгиб с кручениемСкачать

Изгиб с растяжением (сжатием).
При таком виде сложного сопротивления внутренние силовые факторы приводятся к одновременному действию продольной силы N и изгибающего момента M.
Рассмотрим случай центрального растяжения бруса в сочетании с косым изгибом. На консольный брус действует сила F, составляющая некоторый угол с продольной осью бруса и не лежащая ни в одной из главных плоскостей сечения. Сила приложена в центре тяжести торцевого сечения бруса:
К расчёту на прочность бруса при изгибе с растяжением:
a — нагружение бруса; б — внутренние силовые факторы в поперечном сечении;
Разложим силу F на три составляющие. Тогда внутренние силовые факторы приобретут следующий вид:
Напряжение в произвольно выбранной точке Д, имеющей координаты (хд, уд), пренебрегая действием поперечных сил, будут определяться по формуле:
где А — площадь поперечного сечения.
Если сечение имеет две оси симметрии (двутавр, прямоугольник, круг), наибольшее напряжение определяют по формуле:
Условие прочночти имеет вид:
Также как и в случае косого изгиба, если материал бруса не одинаково работает на растяжение и на сжатие, то проверку прочности проводят по допускаемым растягивающим и сжимающим напряжениям.
Видео:КРУЧЕНИЕ ВАЛА. Касательные напряжения. Сопромат.Скачать

Внецентренное растяжение или сжатие.
При таком виде сложного сопротивления продольная сила приложена не в центре тяжести поперечного сечения бруса.
К расчёту на прочность бруса при внецентренном растяжении
a — нагружение бруса; б — внутренние силовые факторы в поперечном сечении;
Приведём силу F к центру тяжести:
где уF , xF — координаты точки приложения силы F.
В произвольной точке Д, с координатами (хд, уд), нормальное напряжение определяется по фомуле:
Условие прочности для бруса, изготовленного из материала, одинаково сопротивляющегося растяжению и сжатию, имеет вид:
Для бруса, который неодинаково работает на растяжение и на сжатие проверка прочности по допускаемым растягивающим и сжимающим напряжениям.
Видео:Расчет вала на прочность и жесткость. Эпюра крутящих моментовСкачать

Кручение с изгибом.
Сочетание деформаций изгиба и кручения характерно для работы валов машин.
Напряжения в сечениях вала возникают от кручения и от изгиба. При изгибе появляются нормальные и касательные напряжения:
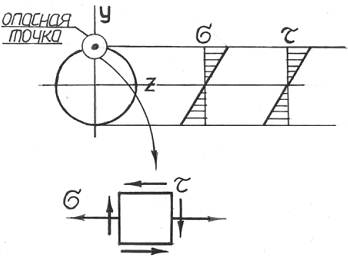
Эпюры напряжений в сечении бруса при кручении с изгибом
Нормальное напряжение достигает максимума на поверхности:
Касательное напряжение от крутящего момента Mz достигает максимума также на поверхности вала:
Из третьей и четвёртой теории прочности:
При кручении с изгибом условие прочности имеет вид:
Видео:Понимание напряжений в балкахСкачать

СЛОЖНОЕ СОПРОТИВЛЕНИЕ. КРУЧЕНИЕ С ИЗГИБОМ
16.1. Общие понятия и определения
Ранее нами был рассмотрен расчет на прочность валов при чистом кручении. Однако круглые валы редко работают на чистое кручение. Как правило, при работе вал изгибается собственным весом, весом шкивов, давлением на зубья шестерен, натяжением ремней и т. д. В таком случае вал будет находиться в условиях сложного сопротивления и испытывать совместное действие кручения и изгиба.
Кручение с изгибом – частный случай сложного сопротивления, который может рассматриваться как сочетание чистого кручения и поперечного изгиба.
Читайте также: Фиксатор распределительного вала 3391
16.2. Определение внутренних усилий и напряжений при кручении с изгибом
Для определения внутренних усилий воспользуемся методом мысленных сечений:
Обычно две составляющие поперечной силы (Qy, Qz) и изгибающего момента (My, Mz) приводят к их полным результирующим
Заметим, что часто поперечной силой пренебрегают (для достаточно длинных валов) и рассматривают кручение с изгибом как совместное действие крутящего (Mx, Mкр, T) и изгибающего (Mи) моментов.
Опасное сечение вала будем искать, как и прежде, по эпюрам внутренних усилий. При построении эпюр внутренних усилий при кручении с изгибом необходимо иметь ввиду следующие правила:
1) эпюры крутящего момента Mx, а также эпюры составляющих поперечной силы Qy, Qz и изгибающего момента My, Mz строятся по той же процедуре, что и ранее;
2) результирующая поперечная сила Q может не лежать в плоскости действия результирующего изгибающего момента Mи, а потому между ними уже не будет соблюдаться зависимость Журавского (dM/dx=Q), а, следовательно, и правила проверки эпюр, введенные для плоского изгиба;
3) согласно (16.1), эпюра полного изгибающего момента будет прямой только на тех участках, где My и Mz ограничены прямыми с общей нулевой точкой, на участках, где такая общая точка отсутствует эпюра Mи будет описываться вогнутой кривой и строится по точкам (связано с тем, что вектор Mи в разных сечениях имеет различное направление).
Опасное сечение при кручении с изгибом устанавливается из совместного анализа эпюр крутящего Mx и полного изгибающего Mи моментов. Опасным будет считаться то сечение, где оба момента достигают своей максимальной величины. Если моменты достигают максимума в разных сечениях, необходимо проверить все сечения, в которых эти внутренние усилия достаточно велики.
Для определения максимальных напряжений ис-пользуем принцип независимости действия сил и найдем напряжения отдельно от кручения и отдельно от изгиба:
а) напряжения при кручении
где Jос – осевой момент инерции для круглого сечения (Jос=Jz=Jy). Вводя обозначение , можем записать
Wос – осевой момент сопротивления для круглого сечения(Wос=Jос/ρmax, ρmax=d/2).
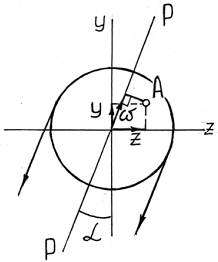
Опасными точками в сечении будут являться точки наиболее удаленные от нейтральной оси (для круглого сечения – линии, перпендикулярной плоскости действия результирующего изгибающего момента). При этом в токах сечения будет возникать плоское напряженное состояние, а потому расчет на прочность необходимо проводить с привлечением известных теорий прочности.
16.3. Определение главных напряжений и расчет на прочность при кручении с изгибом
Подставив величины максимальных нормальных и касательных напряжений в формулу для главных напряжений (σ2=0), получим:
Расчет брусьев при изгибе с кручением проводится с применением теорий прочности. При этом расчет элементов из пластичных материалов выполняется на основе III или IV теорий прочности, а из хрупких – по теории Мора. Проанализируем расчет на прочность по III теории прочности
Подставляя в эту формулу выражения для главных напряжений, получим:
Запишем условие прочности через крутящий и изгибающий моменты, учитывая, что для круглого сечения Wp=2·Wос:
Выражение под корнем называют приведенным (эквивалентным) моментом по третьей теории:
Окончательно условие прочности запишем в виде
Проанализируем расчет на прочность по IV теории прочности
Приведенный (эквивалентный) момент по четвертой теории:
Окончательно условие прочности запишем в виде
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Видео:23. Кручение с изгибом ( практический курс по сопромату )Скачать

Сложное сопротивление. Кручение и изгиб
Шкив с диаметром D1 и с углом наклона ветвей ремня к горизонту α1 делает n оборотов в минуту и передает мощность P кВт. Два других шкива имеют одинаковый диаметр D2, одинаковые углы наклона ветвей ремня к горизонту α2 и каждый из них передает мощность P/2 (рисунок 33). Необходимо подобрать диаметр вала d при [σ] = 100 МПа.
| Номер | Номер | P | n | а | в | с | D1 | D2 | α1 | α2 |
| строки | схемы | кВт | об/мин | м | м | м | м | м | град | град |
| 1 | 1 | 10 | 100 | 1,1 | 1,1 | 1,1 | 1,1 | 1,1 | 10 | 10 |
| 2 | 2 | 20 | 200 | 1,2 | 1,2 | 1,2 | 1,2 | 1,2 | 20 | 20 |
| 3 | 3 | 30 | 300 | 1,3 | 1,3 | 1,3 | 1,3 | 1,3 | 30 | 30 |
| 4 | 4 | 40 | 400 | 1,4 | 1,4 | 1,4 | 1,4 | 1,4 | 40 | 40 |
| 5 | 5 | 50 | 500 | 1,5 | 1,5 | 1,5 | 1,5 | 1,5 | 50 | 50 |
| 6 | 6 | 60 | 600 | 1,6 | 1,6 | 1,6 | 1,6 | 1,6 | 60 | 60 |
| 7 | 7 | 70 | 700 | 1,7 | 1,7 | 1,7 | 1,7 | 1,7 | 70 | 70 |
| 8 | 8 | 80 | 800 | 1,8 | 1,8 | 1,8 | 1,8 | 1,8 | 80 | 80 |
| 9 | 9 | 90 | 900 | 1,9 | 1,9 | 1,9 | 1,9 | 1,9 | 90 | 90 |
| 10 | 100 | 1000 | 2 | 2 | 2 | 2 | 2 | 0 | 0 | |
| Е | Д | В | Г | Д | Б | А | Е | Д | Е |
Читайте также: 70mai автомобильный компрессор xiaomi 70mai air compressor midrive tp01 black
Рисунок 33 − Схемы к задаче 10
УСТОЙЧИВОСТЬ СЖАТЫХ СТЕРЖНЕЙ
Основные понятия
Под действием сжимающей силы стержень может утратить первоначальную форму равновесия и искривиться. Произойдет потеря устойчивости стержня. Наименьшая сила, при которой происходит потеря устойчивости, называется критической и определяется по формуле Эйлера:
Е – модуль упругости материала стержня;
Imin– минимальный осевой момент инерции сечения стержня;
μ – коэффициент приведения длины, зависящий от способа закрепления концов стержня (рисунок 64);
μ ∙ l = lпр – приведенная длина стержня.
Рисунок 34 − Значения коэффициента μ приведенной длины и критической
силы Fкр для сжатых стержней при различных способах закрепления концов
Напряжения, вызванные критической силой, называются критическими и определяются по формуле Эйлера:
где λ – гибкость стержня, ;
– минимальный радиус инерции сечения;
А – площадь поперечного сечения стержня.
Формула Эйлера применима при условии, что критическое напряжение не превышает предела пропорциональности материала σкр. Обычно это условие выражают через гибкость стержня и записывают в виде
где λпр – предельное значение гибкости, которое определяет границу применимости формулы Эйлера.
Формулой Эйлера можно пользоваться, если гибкость стержня λ ≥ λпр,
где а, b , с – коэффициенты, зависящие от материала и имеющие размерность напряжения. Они приведены в таблице 12.
Опытные коэффициенты для определения σкр, МПа
| Материал | а | b | с |
| Сталь Ст3 Сталь Ст5 Чугун Сосна (сжатие вдоль волокон) | 310 464 776 29,3 | 1,14 3,62 12 0,194 | 0 0 0,053 0 |
Критическая сила является недопустимой для сжатых стержней.
Определение допускаемой сжимающей силы [F] производят двумя способами. Первый способ используется, когда для рассчитываемого стержня известны длина, способ закрепления концов, форма и размеры поперечного сечения, материал, коэффициент запаса на устойчивость. Вначале определяют критическую силу Fкр = sкр ∙ А, а затем допускаемую силу [F]: ,
де [nу] – допускаемый коэффициент запаса на устойчивость.
Значения допускаемых коэффициентов запаса на устойчивость [nу] для различных материалов приведены в таблице 13.
Допускаемые коэффициенты запаса на устойчивость для различных материалов
| Материал | [ny] |
| Сталь Ст 3 | 1,8 3 |
| Сталь Ст 5 | 1,8 3 |
| Чугун | 5 5,5 |
| Сосна (сжатие вдоль волокон) | 2,8 3,2 |
Второй способ основан на применении таблиц j (l). Сначала определяют гибкость стержня λ, затем по таблице находят j (l) и вычисляют [F] по формуле: [F] = j (l) . [sс] . А ,
где j(l)– коэффициент уменьшения допускаемого напряжения при сжатии [sс].
Значения коэффициента j в зависимости от гибкости λ и материала стержня приведены в таблице 14.
Для расчета критического напряжения, критической силы, допускаемой сжимающей силы и коэффициента запаса на устойчивость можно использовать блок-схему, представленную на рисунке 35.
Значение коэффициента продольного изгиба j (l)
Практически расчет на устойчивость ведется с использованием коэффициента j – коэффициента уменьшения допускаемого напряжения при сжатии [sс].
Условие устойчивости имеет вид
Читайте также: Датчика положения коленчатого вала ниссан альмера классик
Расчет на устойчивость сводится к недопущению потери устойчивости, т.е. искривления стержня.
Подбор поперечного сечения стержня при заданных длине, сжимающей силе и материале выполняется с использованием таблиц значений j (l) методом последовательных приближений в следующем порядке.
1. Задают произвольное значение j. Например, полагают j = 0,5.
2. Вычисляют допускаемое напряжение на устойчивость:
3. Определяют площадь поперечного сечения из условия
4. Подбирают размеры сечения или номер профиля. Вычисляют
площадь А, минимальный момент инерции Imin, минимальный радиус инерции iminпоперечного сечения.
5. Определяют гибкость стержня l.
6. Если гибкость стержня l > 220, то считают, что заданная сила
F равна допускаемой [F]: ,
где Fкр – критическая сила (определяется по формуле Эйлера), а nу – коэффициент запаса на устойчивость (выбирается по таблице 13).
Тогда можно определить значение наименьшего момента инерции Imin по формуле
7. Если гибкость стержня l 220, то для полученной гибкости
находят истинное значение jи.
8. Вычисляют действующее напряжение s = .
9. Вычисляют допускаемое напряжение [sу] = j и ∙[sс].
10. Сравнивают действующее напряжение с допускаемым, вычисляя относительную разницу k:
11. Если k > 0, то имеем недонапряжение, если k 5%, то в качестве второго приближения берут
j2 = j + jи и повторяют расчет, пока не будет выполняться условие |k| £ 5%.
Подбор сечения по изложенному алгоритму представлен в виде
В сопротивлении стержней продольному изгибу основную роль играет
гибкость стержня и, следовательно, величина наименьшего радиуса инерции сечения, поэтому существенным является вопрос не только величины площади сечения, как при расчете на прочность, но и формы поперечного сечения.
Для наиболее оптимального выбора сечения необходимо конструировать
сечение так, чтобы при определенной площади величина наименьшего радиуса инерции была бы возможно большей. Для этого прежде всего следует стремиться к тому, чтобы центральные моменты инерции сечения были равны. Такой стержень будет оказывать одинаковое сопротивление потере устойчивости в любом направлении.
Далее, необходимо стремиться к получению при данной площади
наибольших центральных моментов инерции. Для этого надо разместить материал сечения по возможности дальше от центра тяжести. Этим условиям хорошо удовлетворяют трубчатое сечение или сечение, составленное из двух швеллеров, раздвинутых на определенное расстояние.
На выбор материала для сжатых стержней влияют два фактора:
1. Если sкр λпр, то Fкр можно определить по формуле Эйлера:
Колонна, составленная из двух швеллеров (рисунок 38), нагружена силой
Рисунок 38 − Подбор поперечного сечения колонны з расчета на устойчивость
Подобрать номер швеллера, если
Сначала нужно выявить главную центральную ось заданного сечения из двух швеллеров с минимальным значением момента инерции. В нашем примере такой осью будет ось симметрии oy (рисунок 38).
Момент инерции произвольного сечения относительно оси oy, параллельной главной оси сечения oy1 и удаленной от нее на расстояние a, можно вычислить по формуле
где площадь сечения.
Так как наша колонна состоит из двух одинаковых швеллеров, состыкованных вплотную друг к другу, то
где А0 – площадь одного швеллера.
Подбор размеров сечения ведется путем последовательного приближения. Обычно задают значение φ и определяют A. Для первого приближения примем произвольно Тогда из условия устойчивости
По сортаменту (ГОСТ 8240 – 72) исследуем швеллер № 10:
Для рассматриваемого сечения, состоящего из двух швеллеров
Гибкость колонны Для стержня с защемленным концом
По таблице для стали марки Ст3, интерполируя, находим истинное значение для выбранного профиля
Перенапряжение составляет 28,4%.
Исследуем швеллер № 12,
Недонапряжение составляет 15,1%.
Анализируя расчеты, заметим, что сечение из двух швеллеров № 10 дает большое перенапряжение, а из двух швеллеров № 12 – существенное недонапряжение. Уменьшить это недонапряжение мы не можем, так как ближайший стандартный профиль с меньшим поперечными размерами – это уже рассмотренный нами швеллер № 10.
Поскольку размеры сечений прокатных профилей от номера к номеру изменяются скачкообразно, во многих случаях не удается подобрать такое сечение, чтобы расхождение в напряжениях не превышало 5 %.
Итак, принимаем сечение из двух швеллеров № 12.
Устойчивость сжатых стержней.
- Свежие записи
- Чем отличается двухтактный мотор от четырехтактного
- Сколько масла заливать в редуктор мотоблока
- Какие моторы бывают у стиральных машин
- Какие валы отсутствуют в двухвальной кпп
- Как снять стопорную шайбу с вала
- Правообладателям
- Политика конфиденциальности
Механика © 2023
Информация, опубликованная на сайте, носит исключительно ознакомительный характер🌟 Видео
11. Кручение ( практический курс по сопромату )Скачать
17. Ломаный брус. Эпюры N, Q, M ( практический курс по сопромату )Скачать
Расчет вала на изгиб с кручениемСкачать
Кручение с изгибом (часть 1)Скачать
Изгиб с кручением пример решения задач по сопротивлению материалов. Теории прочностиСкачать
БАЛКА - 90 СТУДЕНТОВ САМОСТОЯТЕЛЬНО СТРОЯТ ЭПЮРЫ после просмотра этого видео!Скачать
Сопромат. Практическое занятие №1.4Скачать
Основы Сопромата. Виды деформацийСкачать
Кручение. Часть 6 Жесткость валаСкачать
Сопротивление материалов. Лекция: кручение круглого стержняСкачать
22. Косой изгиб ( практический курс по сопромату )Скачать
Кручение валаСкачать