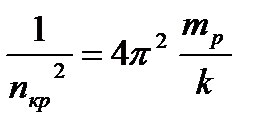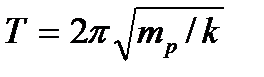Видео:Определение частоты вращения вала мотораСкачать
Собственные частоты колебаний и критические частоты вращения валопровода. Резонансы
Появляющийся прогиб валопровода зависит, прежде всего, от частоты вращения: при постепенном и медленном увеличении частоты вращения прогиб медленно увеличивается, затем резко возрастает, достигая максимума, и снова быстро убывает практически до нуля. Частота вращения, при которой наблюдается резкий всплеск динамического прогиба вала, называется критической, или резонансной.
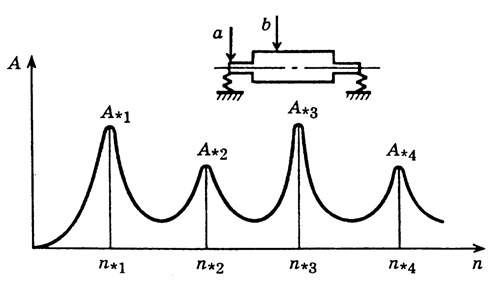
Критические частоты вращения ротора обнаруживаются при снятии амплитудно-частотной характеристики ротора. Если неуравновешенный ротор привести во вращение с переменной частотой и измерить амплитуды А (рис.22.8) колебаний в некоторой точке (точка а или b), то получим характерную кривую, имеющую несколько максимумов. Частоты вращения ротора, при которых амплитуды колебаний достигают максимальных значений – называются критическими.
Рис.22.8 Амплитудно-частотная зависимость колебаний ротора
Наряду с критическими частотами вращения существуют собственные частоты колебаний вращающегося ротора, которые могут быть обнаружены при неизменной частоте вращения и при возбуждении вращающегося с постоянной частотой ротора возбуждающей силой с неизменной амплитудой, но изменяющейся по частоте.
Можно сказать, что критические частоты вращения суть собственные частоты системы ротор – опоры на критических частотах вращения валопровода.
При критических частотах вращения ротора nкр, которые определяются из равенства
, (22.3)
имеет место явление резонанса, когда период вращения колеса на валу совпадает с собственным периодом колебаний системы «вал-турбина». Отсюда, если критическая частота вращения ротора превышает рабочую частоту (nкр>nраб) то ротор (вал) называют жестким, и наоборот, если nкр
Чем больше жесткость конструкции ротора (больше его диаметр и меньше длина), тем большую критическую частоту вращения он имеет. В этой связи жесткие ротора предпочтительней в применении, но в практике из-за больших длин роторов они встречаются редко.
Под вибрационными характеристиками валопровода понимают его критические частоты и соответствующие им главные формы – формы начального изгиба ротора, которые будут давать строго синусоидальные колебания во времени. Воздействие неуравновешенной силы эквивалентно действию двух сил: в горизонтальной и вертикальной плоскостях и изменяющихся во времени, соответственно, по законам косинуса и синуса. Тогда движение центра вала по сложной кривой в пространстве можно представить как наложение движений в горизонтальной и вертикальной плоскостях. Совокупность главной формы колебаний и соответствующей ей частоты называют тоном колебаний. Тон колебаний, отвечающий самой низкой частоте, называют основным. На рис.22.9 показаны три главные формы колебаний для вала, которые являются синусоидами, а соответствующие им частоты собственных колебаний пропорциональны квадрату номера тона колебаний. Обычно интерес представляют первые несколько критических частот, наибольшие значения которых не превышают удвоенной рабочей частоты вращения. Например, для турбины ПТ-80/100-12,8/1,3 ЛМЗ первая критическая частота валопровода nкр1=26,3 с -1 (1580 об/мин), вторая – nкр2=36,9 с -1 (2214 об/мин), третья — nкр3=41,2 с -1 (2470 об/мин).
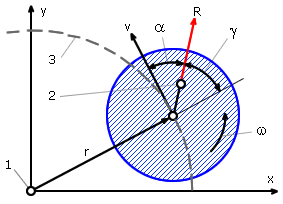
Рабочая частота вращения ротора турбоагрегата должна отличаться от критической с достаточным запасом (± 10-15 %). При совпадении частоты вращения с критическими частотами возникает явление резонанса, сопровождающееся повышенной вибрацией ротора. Известно, что мощность, передаваемая внешней силой телу, равна произведению действующей силы на скорость тела и косинус угла между векторами силы и скорости (рис.22.10): N=Rv×cosa.
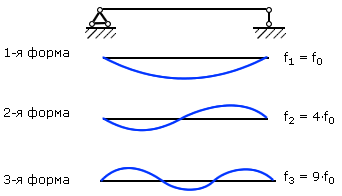
Рис. 22.9. Три главные формы колебаний Рис. 22.10. Движение шейки вала ротора
Читайте также: Какие крестовины карданного вала для нивы лучше
1 — центр вкладыша; 2 — центр масс;
2 — траектория движения центра шейки вала
Максимальный эффект от действия неуравновешенной силы на ротор будет иметь место, когда векторы R и vнаправлены в одну сторону. При малых частотах вращения вектор прогиба вала r будет следовать за возмущающей силой R, т.е. угол g будет равен нулю. С ростом частоты вращения из-за инерции ротора вектор прогиба rвала начнет отставать от вектора возмущающей силы, причем с ростом n отставание будет расти. При критической частоте векторы R и v совпадут, и в этот момент мощность, передаваемая силой валу, будет максимальной. Это и есть момент резонанса. При дальнейшем росте частоты вращения между векторами R и v вновь появится угол и эффект возмущающей силы уменьшится. Итак, причиной повышенной вибрации ротора при резонансе является совпадение направлений действия неуравновешенной силы и скорости прецессионного движения ротора.
Дата добавления: 2017-11-21 ; просмотров: 4890 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Видео:Урок 87 (осн). Вращательное движение. Период и частота вращенияСкачать
Центробежный насос. Резонансная частота и критическая скорость вращения вала.
Joe Evans, Ph.D. December 17, 2011, University of Michigan.
Если Вы думаете, что гидравлика – это сложный предмет, обратите внимание на современную теорию в физике, известную как теория струн. Эта теория претендует на единое объяснение всех фундаментальных основ физики, включая теорию относительности и квантовую механику. Основная гипотеза состоит в том, что все пространство, время и материя представляют собой тонкие струны-частицы, вибрирующие на резонансных частотах. Если теория струн получит подтверждение, мы будем иметь единую унифицированную теорию, объясняющую все.
Вы, наверное, подумали, какой стороной все вышесказанное относится к насосам? Общая точка соприкосновения – резонансная частота. Резонансом в механической системе называют вибрацию с высокой амплитудой, спровоцированную относительно небольшим внешним воздействием частоты с таким же периодом, как и период естественной вибрации самой системы. Другими словами, резонанс – это вибрация в результате, когда один объект, выполненный из упругого материала, подвергается воздействию вибрации на «собственной» частоте. Воздействие может быть механическим или электромагнитным.
Одним из наиболее известных примеров резонанса есть выложенное в Интернете видео с вибрирующим от воздействия голоса певца стаканом из тонкого стекла. Когда певец удерживает голос на частоте собственных колебаний стакана, последний начинает вибрировать и, в конечном счете, разрушается. На современном этапе развития техники этот эксперимент можно повторить, заменив уникальный голос певца на генератор частоты. Увидеть пульсации стекла можно с помощью стробоскопа в замедленной съемке. Этот опыт наглядно может показать начало резонанса и продемонстрировать его разрушительное действие.
Вернемся к насосам. Насколько резонанс и резонансная частота оказывают влияние на применение насосов? Обратим внимание на один из внешних стимулов, который может привести к резонансу во вращательных машинах, к которым относятся центробежные насосы. На сегодняшний день изменение скорости вращения вала насоса часто осуществляется с помощью преобразователя частоты. Так называемые «критические скорости» вращения способны инициировать резонансные частоты.
Отрасль механики с названием «роторная динамика» определяет критическую скорость как угловую скорость, возбуждаемую собственной частотой вращающегося объекта. В случае с валом насоса измеряют скорость вращения, при которой появляется естественная вибрация. Было бы необычно ожидать, что радиальное отклонение вала, вызванное переменным напряжением от веса рабочего колеса, не могло бы привести к вибрации горизонтального насоса даже при условии совершенной балансировки рабочего колеса. Но такие же вибрации имеют место и в вертикальных насосах даже когда вовсе не обнаруживаются радиальные отклонения, вызванные весом колеса.
Читайте также: Замена подшипника в компрессоре кондиционера пассат б6
Причиной увеличивающихся вибраций в роторе с хорошей динамической балансировкой на обычной скорости вращения могут быть небольшие различия в плотности самого ротора и незначительные дефекты его механической обработки. Это приводит к незначительному отклонению центра масс от центральной оси вращения. При наборе скорости вращения упругость металла и радиальные силы создают дисбаланс вращения и приводят к вибрации. Эта вибрация увеличивает отклонение вала, ведет к износу компонентов насоса (механических уплотнений, подшипников, подшипниковых опор, сненных уплотнительных колец), а в отдельных случаях и к разрушению вала. С дальнейшим ростом скорости эта собственная частота исчезает, вибрация прекращается, но на другой более высокой скорости собственная частота снова будет появляться. Наименьшую скорость вращения, при которой появилась естественная вибрация, называют «первой критической скоростью».
В итоге резонанс не является проблемой, когда насосы с коротким жестким валом работают с проектной скоростью вращения. Даже если собственная частота находится в пределах от нуля до полной скорости, ее прохождение при старте осуществляется быстро. Однако, широкое распространение преобразователей частоты заставляет многих принимать во внимание эффект резонансной частоты и критические скорости при работе насоса. Сегодня привычно видеть спецификации инженеров-проектировщиков, требующие обеспечить вращение насоса несколько ниже первой критической скорости. Расчет первой критической скорости – тяжелая задача, но, к счастью, более общие измерения могут привести нас к решению задачи.
Первая критическая скорость вала насоса прямо связана с собственным статическим отклонением, статическим отклонением, обусловленным весом ротора, общей длиной ротора и его диаметром. Фактически отклонение может быть более сложным из-за упругости материала, инерции, зазоров в подшипниковых опорах, вариаций в диаметре вала. Это также принимают во внимание при расчете. К счастью, нам не придется совершать эти вычисления, так как производитель насоса их уже выполнил. Мы должны получить только данные о максимальном статическом отклонении вала от производителя и внести его в простое эмпирическое уравнение:
NC – первая критическая скорость, об/мин;
Большинство производителей насосов устанавливают ограничение отклонения вала от 0,127 до 0,152 мм. При максимальном отклонении 0,152 мм наше уравнение определяет первую критическую скорость, равную 2420 об/мин. Очевидно, что электродвигатели насосов с четырьмя и более полюсами (скорость вращения 1450 об/мин и ниже) работаю значительно ниже значения первой критической скорости, не достигая его. Для того, чтобы первая критическая скорость стала проблемой для 4-х полюсного двигателя, отклонение вращающегося вала должно было бы превышать 0,25 мм.
Насос с отклонением вала в 0,152 мм, приводимый в действие двухполюсным асинхронным двигателем (≈2950 об/мин) будет работать со скоростью, которая значительно превышает первую критическую скорость. Как сказано ранее это не представляет проблему в задачах с постоянной скоростью, так как вал проходит через критическую скорость очень быстро. Даже плавный пуск, обеспечиваемый преобразователем частоты, не оказывает влияние, так как время набора скорости остается достаточно коротким.
Читайте также: Воздушный поршневой безмасляный компрессор аэрус 180 6
Однако, проблема появляется тогда, когда критическая скорость находится в пределах требуемого диапазона скорости. К счастью, большинство современных преобразователей частоты могут программироваться на обход отдельных диапазонов частот. Например, если критическая скорость находится в пределах 41-43 Гц, преобразователь частоты будет пропускать эти частоты и заменять их на 40 или 44 Гц соответственно. Вал насоса будет проходить критическую скорость, но преобразователь частоты не будет позволять удерживать эту скорость.
Также стоит отметить то, что приведенное уравнение используется для расчета критической скорости ротора в воздухе. При работе в жидкости вокруг вала и рабочего колеса возникают определенные гидродинамические силы, которые могут обеспечить дополнительную стабильность и валу, и рабочему колесу. Эти, известные под названием «центрирующий эффект Ломакина-Этингера», гидродинамические силы могут снижать отклонение и увеличивать первую критическую скорость до значения, значительно превышающего расчетное.
Видео:Физика.Узнать за 2 минуты.Основные понятия.Что такое частотаСкачать
Собственная частота вращения вала
Валы (роторы) являются одним из наиболее распространенных элементов машин. При расчете вал рассматривается как стержень. Такая модель пригодна для большинства валов. Исключение могут составить тонкостенные полые валы (роторы), для которых оказываются существенными оболочечные эффекты, и очень короткие валы, где следует учитывать пространственное напряженное состояние.
При построении динамических моделей валов следует учитывать критические частоты вращения и возможность крутильных колебаний.
Рис. 12.16. Критическая частота вращения двухопорного вала с диском посредине: а — идеально уравновешенный диск; б — диск с начальным эксцентриситетом
Понятие о критической частоте вращения.
Рассмотрим вращение двухопорного вала с диском посредине (рис. 12.16). Для того чтобы выяснить, является ли вращение вала с прямолинейной осью устойчивым, дадим ему некоторое отклонение v. Центр тяжести диска будет двигаться по окружности радиусом v, и возникнет центробежная сила
где — частота вращения вала ; — масса диска. Отклонение вала приведет к появлению силы упругости, стремящейся вернуть вал в не деформированное состояние:
где — прогиб сечения вала от единичной силы в том же сечении.
Для вала постоянного сечения (см. разд. 42)
где — момент инерции поперечного сечения (индекс опускается, так как сечение вала предполагается круглым). Пренебрегая весом диска, можно заключить, что при вращение вала будет устойчивым, так как после отклонения вал вернется в первоначальное положение. В момент равновесия, когда прогибы вала могут неограниченно возрастать: в любом отклоненном положении центробежные силы и восстанавливающие силы упругости равны.
Частота вращения вала, при которой наступает равенство центробежных сил и сил упругости при отклоненном положении вала, называется критической. Приравнивая значения С и F, находим
Критическая частота вращения (в оборотах в минуту) равна
Можно представить, что при критической частоте вращения вал совершенно теряет жесткость на изгиб — даже малая внешняя сила может вызвать опасные прогибы.
Замечание. Из равенства (115) и формулы (14) получается, что критическая частота вращения вала равна круговой частоте собственных изгибных колебаний. Этот вывод справедлив и в более общих случаях (вал с распределенными массами и т. п.), если детали, закрепленные на валу, рассматриваются как точечные массы, т. е. когда пренебрегают инерцией поворота.
- Свежие записи
- Чем отличается двухтактный мотор от четырехтактного
- Сколько масла заливать в редуктор мотоблока
- Какие моторы бывают у стиральных машин
- Какие валы отсутствуют в двухвальной кпп
- Как снять стопорную шайбу с вала
- Правообладателям
- Политика конфиденциальности
🔍 Видео
Ременная передача. Урок №3Скачать
Работает датчик частоты вращения валаСкачать
Определение резонансной частоты колебательного контураСкачать
Датчик частоты вращения выходного вала MMC Pagero 2 датчик частоты вращения выходного вала митсубисиСкачать
Гибкий валСкачать
Урок 44. Вращение твердого тела. Линейная и угловая скорость. Период и частота вращения.Скачать
Наглядное сравнение частоты вращения различных орудий расчистки под разные задачиСкачать
Собственные частоты колебаний точкиСкачать
Измерение частоты вращения стробоскопическим тахометром ChipTip StrobeСкачать
Как посчитать обороты и передаточное число.Скачать
Измерение числа оборотов двигателя в домашних условияхСкачать
Датчик частоты вращения входного вала акппСкачать
Преодоление ХРОНИЧЕСКИХ заболеваний - поиск причины и решениеСкачать
Замена датчика частоты вращения входного вала АКПП FN4A-EL на Mazda Demio. Ошибка P0715Скачать
Кадыров уволил и отправил домойСкачать
как сменить датчик частоты вращения входного вала КПП ,Мазда 6Скачать
ТЕХНИКА БЕЗОПАСНОСТИ. Вид Грубейшего Нарушения ТРЕБОВАНИЙ ТБ при работе на СТАНКАХ.Скачать
