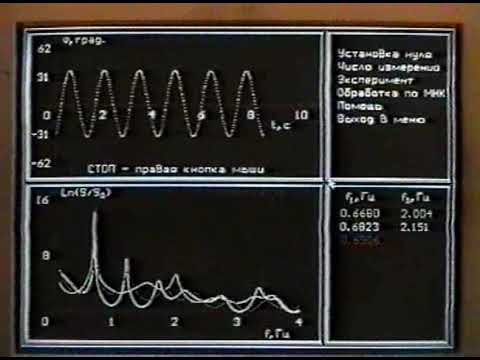
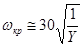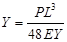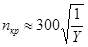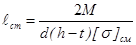Описываются факторы — влияющие на частоту собственных колебаний вала насоса . Рассматриваются колебания вала с учетом гидродинамических сил в уплотнениях и сил магнитного притяжения в электродвигателе. Показывается влияние гидростатических подшипников. [8]
Эта сила приводит к некоторому изменению частоты собственных колебаний вала . Очевидно, что растягивающая сила увеличивает частоту колебаний, а сжимающая уменьшает ее. [9]
Обычно в качестве резонансной частоты рассматривают частоту собственных колебаний недемпфированного вала , хотя известно, что максимум перемещений получается под влиянием демпфирования при более низкой частоте колебаний. Однако различие между этими двумя частотами колебаний при обычном демпфировании незначительно. [10]
С / т ю2 — есть квадрат частоты собственных колебаний вала . [12]
Если частота возмущающих сил совпадает или кратна частоте собственных колебаний вала ( оси), то при критической частоте вращения ( пк) возникает резонанс. Различают несколько разновидностей колебаний валов и осей: поперечные ( изгибные) колебания, угловые ( крутильные) и изгибно-крутильные. Последние две разновидности колебаний характерны для специальных устройств ( турбины, буровые станки и др.) и рассмотрены в особых курсах. [13]
Потеря устойчивости движения ротора возможна также при совпадении частоты собственных колебаний вала ротора с угловой скоростью распространения волны в жидкости. [14]
Видео:Свободные колебания механических систем, 1972Скачать
Расчет валов на колебания
Для большинства быстроходных валов причинами, вызывающими колебания являются силы от неуравновешенных масс деталей. При совпадении или кратности частоты возмущающей силы и частоты собственных колебаний вала наступает явление резонанса, при котором амплитуда колебаний вала резко возрастает и может достигнуть опасных значений. Соответствующие резонансу угловую скорость (ω) и частоту вращения (n) называют критическими (ωкр, nкр).
Различают следующие виды колебаний валов: поперечные или изгибные угловые или крутильные; и изгибно-крутильные. В курсе ДМ рассматривают только поперечные колебания, а остальные – в специальных курсах.
Расчет осей и валов на поперечные колебания заключается в проверке условия отсутствия резонанса при установившемся режиме.
Читайте также: Вибрация от карданного вала газель
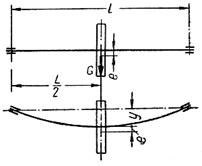
Рис. 20.6. Схема для определения критической частоты
Исследованиями установлено, что для отсутствия явления резонанса скорость вращения оси или вала при установившемся движении должна быть меньше или больше критической скорости.
,
где Y – прогиб вала от действия веса установленных на нем деталей.
Например, для простейшей схемы, когда на валу симметрично относительно опор установлена деталь, весом (Р) со смещенным центром тяжести на величину (е).
.
Критическое число оборотов равно:
.
О приближении скорости вращения вала к критической можно судить по появлению увеличивающейся вибрации вала.
Большинство валов и осей работают в докритической области. Для уменьшения опасности резонанса повышают жесткость валов и уменьшают их частоту вращения n ≤ 0,7 nкр.
При больших скоростях вращения применяют валы (турбины, центрифуги), работающие в закритической области. Сами валы изготавливают повышенной податливости, кроме того, принимают n ≥ 0,7 nкр.
Переход через ωкр осуществляют возможно быстрее и предусматривают специальные ограничители колебаний.
20.14. К определению расстоянии между опорами
ведомого вала
Расстояние между опорами вала:
где ℓст не меньше b = ψа ·аW + 3…6. (мм) или из условия прочности шпоночного соединения
.
Длина ступицы должна быть согласована с диаметром вала ℓст ≈ (0,8…1,5)d чаще всего ℓст ≈ 1,2d;
х – зазор между ступицей и внутренними стенками корпуса х ≈ 5…100 мм;
W – ширина бобышки в корпусе под подшипник (по табл. 25…50 мм);
f – в том же диапазоне 50…100 мм.
Видео:МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ период колебаний частота колебанийСкачать
Собственные колебания вала это
Видео:Собственные частоты колебаний точкиСкачать
ОСНОВНЫЕ ПОНЯТИЯ О КОЛЕБАНИЯХ КОЛЕНЧАТОГО ВАЛА
Для коленчатых валов автомобильных двигателей наибольшую опасность представляют крутильные колебания, хотя и изгибные колебания в некоторых конструкциях могут привести кполомкеколенчатоговала.
Крутильные колебания опасны не только для деталей криво-шипно-шатунного механизма, но также и для всех механических передач, соединенных упругой связью с коленчатым валом. Поэтому при проектировании двигателей и механических передач всю систему (двигатель + трансмиссия) рассчитывают на крутильныеколебания.
Крутильные колебания вызываются периодическими изменениями тангенциальных сил, приложенных к коленам вала двигателя, и являются следствием крутильной упругости вала.
Для упрощения расчета действительную крутильную систему заменяют эквивалентной (рис. 175, а и б). Последняя представляет собой вал постоянного диаметра,не обладающий массой, с насаженными на нем дисками (сосредоточенными массами) с моментами инерции JuJt, …, заменяющими связанные с валом массы.
Действительная и эквивалентная системы имеют одинаковые частоты собственных (свободных) колебаний и почти точное совпадение форм этих колебаний.
Частотой собственных колебаний системы вала называются частота, с которой колеблется выведенная из покоя система без воздействия внешних сил. Система вала с к дисками имеет к—1 частот собственных колебаний. Если систему вывести из покоя произвольным образом (например, закрутить вал за концы в противоположные стороны и осовободить его), то одновременно возникнут собственные колебания с различной частотой, наложенные одно на другое.
Амплитудой колебаний (в радианах или градусах) называется наибольшее угловое отклонение колеблющегося диска от положения покоя.
Читайте также: Датчик положения коленчатого вала тигуан
Формой колебаний вала называется график амплитудных отклонений масс от положения покоя по длине эквивалентного вала.
Каждой частоте собственных колебаний соответствует определенная форма колебаний. Те сечения вала, которые при колебаниях не отклоняются от положения покоя, называются узлами колебания.
Форма колебаний обозначается по числу узлов (одноузло-вая форма, двухузловая форма и т. д.). Форма с самой высокой для «йстемы из к масс частотой колебаний имеет к — 1 узлов.
Отдельные свободные колебания масс на валу для данной формы могут быть гармоническими. При этом деформация валов должна быть прямо пропорциональна приложенному моменту. Если на валу установлена муфта с резиновыми элементами (предварительно сжатыми пружинами и т. п.) и зависимость угла закручивания вала от момента нелинейна, то колебания системы не будут гармоническими.
Крутящий момент, под действием которого вращается коленчатый вал, можно рассматривать, пользуясь методами гармонического анализа, как состоящий из суммы синусоидальных моментов (гармоник) с различными частотой, амплитудой и фазой.
Число периодов гармоники, приходящееся на один оборот двигателя, называется порядком гармоники. Так как основной период крутящего момента в четырехтактном двигателе равен двум оборотам, то полученные из гармонического анализа крутящего момента гармоники с периодами 1, 2, 3 … обозначаются как гармоники 1/2-го, 1-го, 1*/2-го … порядков; для двухтактных двигателей дробных порядковнет.
Вынужденные колебания системы вала под действием крутящего момента рассматривают как сумму гармонических колебаний, вызываемыхгармоникамиотдельныхпорядков.
Резонансными колебаниями называются колебания под действием гармоники какого-либо порядка, частота которой равна частоте собственных колебаний системы. Возникающие при резонансе сильные (вынужденные) колебания системы образуют форму, практически совпадающую с формой собственных колебаний соответствующей частоты. Поэтому различают резонанс одноузловой формы, двухузловой и т. д., рассматривая его Как результат действия возбуждающих сил и обозначают как резонанс гармоники 1/2-го порядка, резонанс гармоники 4V2-roпорядка и т. д.
Число оборотов двигателя, при котором возникает резонанс, называют резонансным числом оборотов (рис. 175, г).
Резонансы крутильных колебаний в рабочем диапазоне оборотов коленчатого вала двигателя являются не только нежелательными, но и в ряде случаев недопустимыми. При работе двигателе на резонансном режиме наблюдаетсяследующее:
1.Работа двигателя сопровождается усилением стуков и вибрации как самого двигателя, так и основания; при этом заметныевибрации ощущаются и в кузове автомобиля.
При увеличении или уменьшении числа оборотов коленчатого вала неприятные стуки и вибрации в двигателе уменьшаются или исчезают совсем.
2.Нагреваются отдельные участки коленчатого вала. Это явление чаще всего возникает в валах приводов от стационарных двигателей, если энергия крутильных колебаний расходуется на работу внутреннего (межмолекулярного) трения.
3.Уменьшается мощность двигателя при увеличении числа оборотов коленчатого вала. Это объясняется наличием в системе коленчатого вала крутильных колебаний, при которых некоторая часть мощности двигателя затрачивается на работу внутреннего межмолекулярного трения, а также на работу внешнего трения, возникающего при этих колебаниях и вибрации двигателя в целом.
Читайте также: Карданные валы краз размеры
Способы устранения колебаний могут быть различными. К ним относятся: 1) увеличение или уменьшение частот собственных колебаний системы путем изменения конструкции двигателя (увеличение или уменьшение движущихся масс или жесткостей участков между массами); 2) изменение работы возбуждающих моментов путем выбора другого порядка работы двигателя; 3) постановка специальных устройств (гасителей, или демпферов) для гашения крутильных колебаний.
Первые две меры борьбы с крутильными колебаниями весьма органичены посвоимвозможностям,атретья — универсальна.
Гасители крутильных колебаний можно разделить на три группы: 1) устройства, поглощающие энергию, подводимую возбуждающим моментом, вследствие чего уменьшается амплитуда колебаний; к этой группе относятся гасители сухого трения, гидравлические и ударные; 2) устройства, уравновешивающие возбуждающий момент или изменяющие частоту системы без рассеяния энергии; к ним относятся добавочные массы на пружине (динамический гаситель, устройства для отключения маховых масс при приближении к резонансу, муфты, маятниковые гасители); 3) смешанные устройства, действие которых основано частично на изменении жесткости системы или уравновешивании возбуждающего момента, частично на рассеянии энергии: резиновые гасители, динамические гасители с рессорными пружинами и др.
Широкое применение в автомобильных двигателях получили резиновые гасители крутильных колебаний (рис. 175, д). Маховая масса 1 в этом гасителе присоединена к кожуху 3 через слой резины 2. Резина одновременно является элементом, рассеивающим энергию, и пружиной, с помощью которой к системе присоединяется маховая масса.
Видео:Собственные колебания физического маятникаСкачать
Расчеты валов на колебания
В колебаниях, наблюдаемых в машинах, обычно участвует значительная часть системы, в частности основная кинематическая цепь машины, основные несущие детали.
Основное практическое значение для валов имеют расчеты частот собственных колебаний для предотвращения резонанса колебаний, т. е. нарастания амплитуд колебаний при совпадении или кратности частоты возмущающих сил и собственной частоты колебаний. В валах наблюдаются: поперечные или изгибные колебания, угловые или крутильные колебания, а также изгибно-крутильные колебания.
Наибольшее распространение имеют расчеты основных частот колебаний, так как эти колебания обычно являются наиболее опасными.
Основная частота собственных колебаний валов и осей может быть определена по формуле
где Wi — вес насаженных на вал деталей и отдельных участков вала; yi — прогибы вала от всей нагрузки (с учетом упругих перемещений в опорах) в сечениях действия Wi; g — ускорение силы тяжести.
Как известно из теории колебаний, после перехода через критические частоты вращения наступает динамическое центрирование вала. Большинство валов работает в дорезонансной зоне, причем для уменьшения опасности резонанса повышают их жесткость и, следовательно, собственные частоты колебаний. при больших частотах вращения, например в быстроходных турбинах и центрифугах, применяют валы, работающие в зарезанансной зоне. для того чтобы отойти от области резонанса, валы делают повышенной податливости. Проход через критические частоты вращения во избежание аварий осуществляют с возможно большей скоростью; применяют специальные ограничители амплитуд колебаний; быстровращающиеся детали тщательно балансируют.
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
- Свежие записи
- Чем отличается двухтактный мотор от четырехтактного
- Сколько масла заливать в редуктор мотоблока
- Какие моторы бывают у стиральных машин
- Какие валы отсутствуют в двухвальной кпп
- Как снять стопорную шайбу с вала
🎦 Видео
Расчет коленчатого вала на крутильные колебания с использованием среды MATLABСкачать
Расчет собственных частот и форм колебаний металлоконструкцииСкачать
Анализ частот собственных колебанийСкачать
Свободные колебания многомассовой системыСкачать
Свободные электромагнитные колебания. 11 класс.Скачать
Свободные колебания двухмассовой системыСкачать
Основы динамических расчет в ЛИРА САПР | Собственные колебания стойкиСкачать
Простая рама. Определение частот и форм собственных колебаний системы с сосредоточенными массамиСкачать
19.05.2023 Собственные частоты, колебанияСкачать
Зависимость частоты собственных колебаний маятника от амплитудыСкачать
Расчёт собственных частот и форм колебаний опорных и пролётных конструкций дорожных эстакадСкачать
Зависимость частоты собственных колебаний маятника от амплитудыСкачать
Зависимость частоты собственных колебаний маятника от амплитудыСкачать
Расчёт на динамические воздействия в Lira Sapr Урок 2 Колебания плоской рамыСкачать
Урок 333. "Энергетический" метод расчета частоты свободных колебанийСкачать
Логос 5.3.23: Циклическая симметрия. Собственные частоты циклически симметричной конструкции.Скачать
