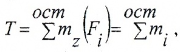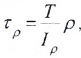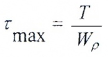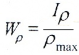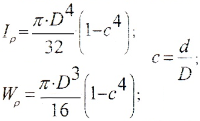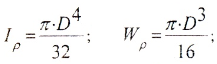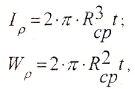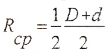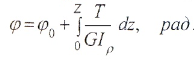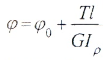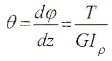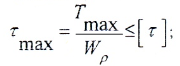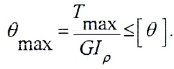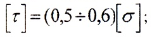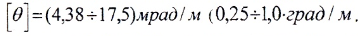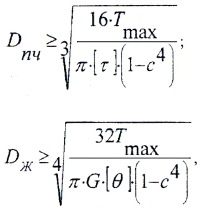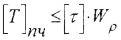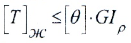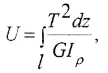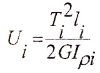Участок вала не испытывающий кручение это (2 видео)

Кручением называется такой вид деформации бруса, при котором в его поперечных сечениях возникает только один внутренний силовой фактор – крутящий момент T.

Брусья, испытывающие кручение, принято называть валами.

Содержание

Внутренний крутящий момент
Напряжения при кручении
Деформации
Тема 2.4. Кручение
КРУЧЕНИЕ
💥 Видео

Видео:Кручение валаСкачать

Внутренний крутящий момент

Внутренние скручивающие моменты появляются под действием внешних крутящих моментов m_i, расположенных в плоскостях, перпендикулярных к продольной оси бруса.

Скручивающие моменты передаются на вал в местах посадки зубчатых колес, шкивов ременных передач и т.п.

Величина крутящего момента в любом сечении вала определяется методом сечений:

т.е. крутящий момент численно равен алгебраической сумме скручивающих моментов m_i, расположенных по одну сторону от рассматриваемого сечения.

Правило знаков внутренних скручивающих моментов:
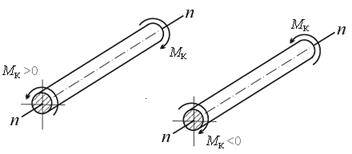
Положительными принимаются внутренние моменты, стремящиеся повернуть рассматриваемую часть вала против хода часовой стрелки, при рассмотрении со стороны отброшенной части вала.

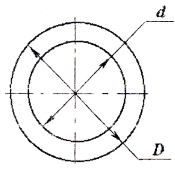
В технике наиболее широко используются валы круглого поперечного сечения.

Теория кручения круглых валов основана на следующих гипотезах:

поперечное сечение, плоское до деформации вала, остается плоским и после деформации;
радиусы, проведенные мысленно в любом поперечном сечении, в процессе деформации вала не искривляются.

Видео:КРУЧЕНИЕ ВАЛА. Касательные напряжения. Сопромат.Скачать

Напряжения при кручении

В поперечных сечениях вала при кручении имеют место только касательные напряжения.
Касательные напряжения, направленные перпендикулярно к радиусам, для произвольной точки, отстоящей на расстоянии ρ от центра, вычисляются по формуле:

где I_ρ — полярный момент инерции.
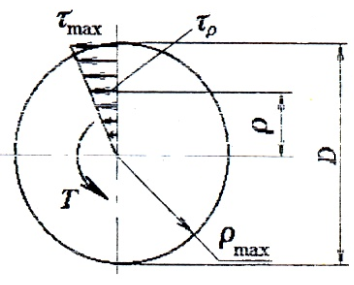
Эпюра касательных напряжений при кручении имеет следующий вид:

Касательные напряжения меняются по линейному закону и достигают максимального значения на контуре сечения при ρ= ρ_max:

Здесь:

— полярный момент сопротивления.
Геометрические характеристики сечений:
а) для полого вала:

б) для вала сплошного сечения (c=0)

в) для тонкостенной трубы (t 0,9)

где

— радиус срединной поверхности трубы.

Видео:Расчет вала на прочность и жесткость. Эпюра крутящих моментовСкачать

Деформации

Деформации валов при кручении заключаются в повороте одного сечения относительно другого.

Угол закручивания вала на длине Z определяется по формуле:

Если крутящий момент и величина GI_ρ, называемая жесткостью поперечного сечения при кручении, постоянны, для участка вала длиной l имеем:

Угол закручивания, приходящийся на единицу длины, называют относительным углом закручивания:

Расчет валов сводится к одновременному выполнению двух условий:

условию прочности:
условию жесткости:

Для стальных валов принимается:

допускаемое касательное напряжение
допускаемый относительный угол закручивания

Используя условия прочности и жесткости, как и при растяжении – сжатии можно решать три типа задач:

проверочный расчет, заключающийся в проверке выполнения условий прочности и жесткости при известных значениях крутящего момента, размеров и материала вала.
Проектировочный расчет, при котором вычисляются диаметры:

при этом берется большее из найденных значений, а затем принимается стандартное значение по ГОСТ.
Определение грузоподъемности вала:
- из условия прочности
- из условия жесткости

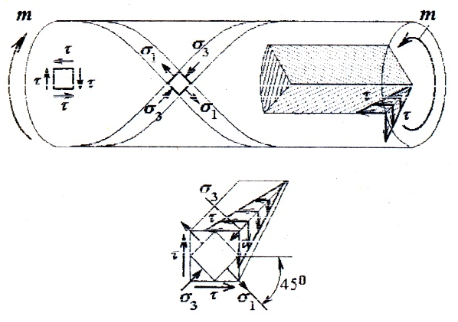
При кручении, наряду с касательными напряжениями в поперечных сечениях, в соответствии с законом парности, касательные напряжения возникают и в продольных сечениях. Таким образом, во всех точках вала имеет место чистый сдвиг.

Главные напряжения σ₁ = τ, σ₃ = -τ наклонены под углом α=±45 о к образующей.

Потенциальная энергия упругой деформации определяется по формуле

или для участка вала при постоянном T и GI_ρ

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Видео:КРУЧЕНИЕ. ЭПЮРЫ ЗАКРУЧИВАНИЯ. Углы поворота. СопроматСкачать

Тема 2.4. Кручение

Под кручением понимается такой вид деформации, когда в поперечных сечениях бруса действует только крутящий момент M_k, (другое обозначение T, M_z), а остальные силовые факторы (нормальная и поперечная силы и изгибающие моменты) отсутствуют.

Или другое определение кручением называют деформацию, возникающую при действии на стержень пары сил, расположенной в плоскости, перпендикулярной к его оси (рис.1).

Кручение возникает в валах, винтовых пружинах, в элементах пространственных конструкций и т.п.

Деформация кручения наблюдается если прямой брус нагружен внешними моментами (парами сил M), плоскости действия которых перпендикулярны к его продольной оси

В чистом виде деформация кручения встречается редко, обычно присутствуют и другие внутренние силовые факторы (изгибающие моменты, продольные силы).

Стержни круглого или кольцевого сечения, работающие на кручение, называют валами.

Внешние крутящие моменты передаются на вал в местах посадки на него шкивов, зубчатых колес, там, где поперечная нагрузка смещена относительно оси вала.

Мы будем рассматривать прямой брус только в состоянии покоя или равномерного вращения. В этом случае алгебраическая сумма всех внешних скручивающих моментов, приложенных к брусу, будет равна нулю.

При расчете брусьев, испытывающий деформацию кручения, на прочность и жесткость при статическом действии нагрузки, надо решить две основные задачи. Это определение напряжений (от M_k), возникающих в брусе, и нахождение угловых перемещений в зависимости от внешних скручивающих моментов.

При расчете валов обычно бывает известна мощность, передаваемая на вал, а величины внешних скручивающих моментов, подлежат определению. Внешние скручивающие моменты, как правило, передаются на вал в местах посадки на него шкивов, зубчатых колес и т.п.

В ряде случаев величины внешних крутящих моментов определяются по величине потребляемой мощности и по скорости вращения вала. Если вал делает в минуту n оборотов (n- частота вращения, единицы измерения — об/мин.), то вращающий момент можно найти по формуле: М_вр=P/n,

эта формула дает значение момента в Н·м, если мощность выражена в Вт, а частота вращения n — об/мин.

§2. Построение эпюр крутящих моментов

Для определения напряжений и деформаций вала необходимо знать значения внутренних крутящих моментов M_k (M_z) в поперечных сечениях по длине вала. Диаграмму, показывающую распределение значений крутящих моментов по длине бруса, называют эпюрой крутящих моментов. Зная величины внешних скручивающих моментов и используя метод сечений, мы можем определить крутящие моменты, возникающие в поперечных сечениях вала.

В простейшем случае, когда вал нагружен только двумя внешними моментами (эти моменты из условия равновесия вала ΣM_z=0 всегда равны друг другу по величине и направлены в противоположные стороны), как показано на рис. 1, крутящий момент M_z в любом поперечном сечении вала (на участке между внешними моментами) по величине равен внешнему моменту |M₁|=|M₂|.

Видео:11. Кручение ( практический курс по сопромату )Скачать

КРУЧЕНИЕ

ОСНОВНЫЕ ПОНЯТИЯ. КРУТЯЩИЕ МОМЕНТЫ И ИХ ЭПЮРЫ

Кручение – это такой вид нагружения стержня, при котором в его поперечных сечениях возникает единственный внутренний силовой фактор — крутящий момент, обозначаемый M_к (или М_z).Стержень, работающий на кручение, называют валом.

Деформация кручения возникает при нагружении стержня парами сил, плоскости действия которых перпендикулярны к его продольной оси. Моменты этих пар будем называть скручивающими и обозначать буквой М.

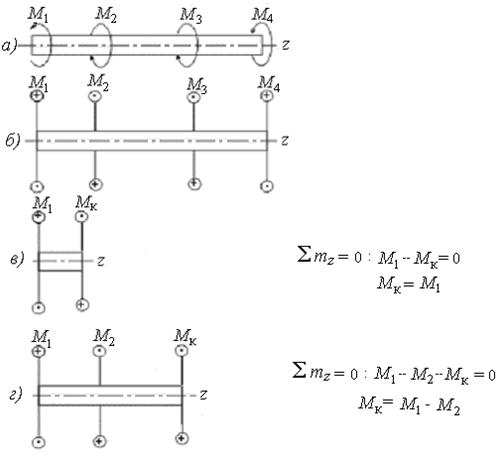
На рис. 6.1,а представлен вал, работающий на кручение под действием приложенных к нему скручивающих моментов. При этом на рис. 6.1,б внешний момент условно изображён в виде двух кружков: кружок с точкой обозначает силу, направленную на наблюдателя, а кружок с крестом – силу, направленную от наблюдателя.

Во всех случаях будем считать, что алгебраическая сумма скручивающих моментов равна нулю, т.е. вал находится в равновесии.

Условимся о следующем правиле знаков: крутящий момент считается положительным, если при взгляде на сечение со стороны внешней нормали п он направлен против хода часовой стрелки (рис. 6.2). Соответствующий внешний скручивающий момент направлен по ходу часовой стрелки.

Применяя метод сечений и рассматривая равновесие отсечённой части (рис. 6.1,в,г), приходим к выводу, что крутящий момент в произвольном поперечном сечении вала численно равен алгебраической сумме скручивающих моментов, приложенных к отсечённой части:

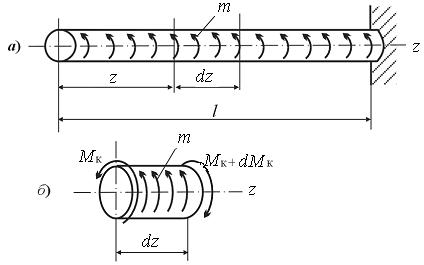
Помимо сосредоточенных скручивающих моментов на вал может действовать и распределённая по некоторому закону моментная нагрузка интенсивностью m(z).

Установим дифференциальную зависимость между интенсивностью m и крутящим моментом М_к. Для этого рассмотрим стержень с моментной нагрузкой m (рис. 6.3,а), из которого вырежем элемент длиной dz (рис. 6.3,б)

На него будут действовать моментная нагрузка m = const, которую можно считать равномерно распределённой ввиду малости dz, и уравновешивающие положительные крутящие моменты (в левом сечении – М_к, в правом – М_к+dМ_к, где dМ_к – приращение крутящего момента). Составим уравнение равновесия для элемента:

График, показывающий закон изменения крутящих моментов по длине вала, называется эпюрой крутящих моментов. Положительные значения на эпюре будем откладывать вверх от горизонтальной базисной линии, а отрицательные значения – вниз. Построение эпюры крутящих моментов принципиально ничем не отличается от построения эпюры продольных сил.

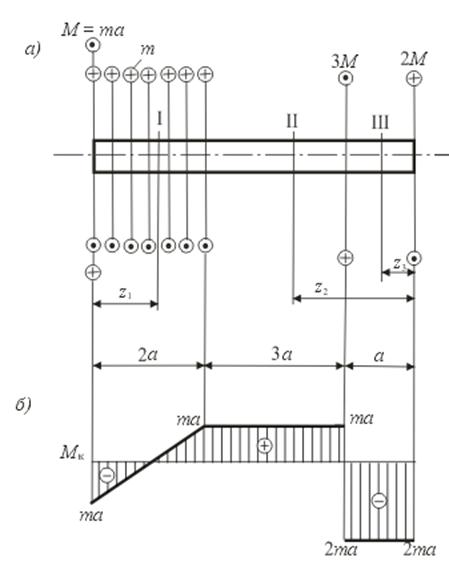
Пример. Построить эпюру крутящих моментов для вала, изображённого на рис. 6.4,а.

Решение. Разбиваем вал на три участка: I, II, III. Используя метод сечений, на участке I мысленно проводим в произвольном месте сечение, отбрасываем правую часть вала и рассматриваем равновесие отсечённой левой части с приложенным в месте сечения положительным крутящим моментом М_к и внешней нагрузкой. Тогда в соответствие с принятым правилом знаков для участка I получаем

Проведя произвольные сечения на остальных участках вала, получим соответственно:

II. (отбрасываем левую часть);

III. (отбрасываем левую часть);

По полученным данным строим эпюру М_к (рис. 6.4,б). На участке I величина крутящего момента линейно зависит от координаты сечения, так как действует равномерно распределённая моментная нагрузка интенсивностью m. На участках I и II крутящий момент не зависит от координаты z, поэтому эпюра имеет вид прямоугольников. В тех сечениях, где приложены внешние сосредоточенные моменты, получаются скачки на величину этих моментов.

НАПРЯЖЕНИЯ И ДЕФОРМАЦИИ ПРИ КРУЧЕНИИ ВАЛА КРУГЛОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ

Теория кручения вала круглого сплошного или кольцевого поперечного сечения основана на следующих допущениях, подтверждаемых экспериментально:

1. Сечения, плоские и нормальные к оси вала до деформации, остаются плоскими и нормальными к его оси и после деформации (гипотеза плоских сечений).

2. Радиусы, проведённые в сечении, остаются прямыми и поворачиваются на один и тот же угол.

3. Расстояния между поперечными сечениями не изменяются, т.е. продольные волокна не удлиняются и не укорачиваются.

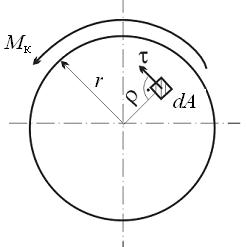
Согласно принятым допущениям, кручение представляет деформацию сдвига материала, заключённого между соседними поперечными сечениями, вызванную относительным поворотом этих сечений вокруг оси z. Вследствие этого в поперечных сечениях действуют только касательные напряжения τ, направленные перпендикулярно соответствующему радиусу (рис. 6.5).

Крутящий момент в сечении, являющийся результирующим моментом внутренних касательных сил, действующих на элементарных площадках dA, расположенных на расстоянии ρ от центра сечения, можно выразить уравнением

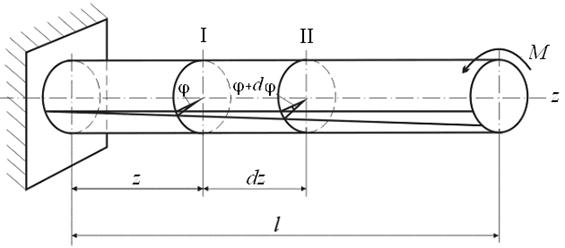
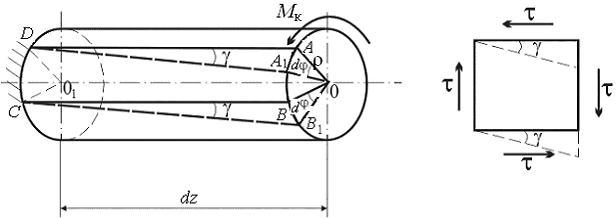
Характер распределения напряжений по сечению установим из геометрической картины деформации вала. Для этого из исследуемого вала (рис. 6.6) выделим элементарный цилиндр двумя бесконечно близкими сечениями I и II произвольного радиуса ρ. Пусть φ – угол закручивания сечения I относительно заделки, φ+dφ – сечения II. Следовательно, угол закручивания участка вала длиной dz равен dφ.

С использованием указанных допущений изобразим деформацию элементарного цилиндра, условно закрепив левое сечение (рис.6.7).

Рассмотрим деформацию прямоугольного элемента ABCD бесконечно малой толщины. Радиусы ОА и ОВ, оставаясь прямыми, повернутся на угол dφ и займут положение соответственно ОА₁ и ОВ₁. При этом образующие АD и ВС перейдут в новое положение А₁D и В₁С составив с первоначальным угол g. Так как длина этих отрезков практически неизменна, то деформация элемента состоит в изменении первоначально прямых углов на величину угла g. Таким образом, рассмотренный элемент находится в условиях чистого сдвига, и на его гранях действуют касательные напряжения. Здесь g является углом сдвига и

Учитывая, что АА₁ = ρdφ, АD = dz, получаем

Величина называется относительным (погонным) углом закручивания и имеет размерность рад/м. Учитывая это, формулу (6.4) можно записать так:

По закону Гука при чистом сдвиге получим

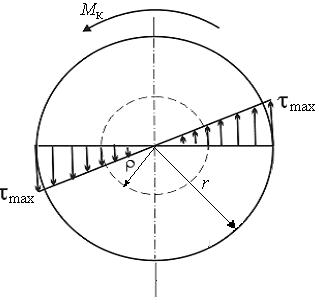
где G и — константы для всех точек сечения и, следовательно, касательные напряжения в поперечном сечении изменяются по линейному закону прямо пропорционально расстоянию ρ точек от центра сечения. Покажем эпюру касательных напряжений в сечении (рис.6.8). Во всех точках окружности радиуса ρ напряжение τ = const и направлено по касательной к окружности. Очевидно максимальные напряжения будут у поверхности вала при ρ = r.

Таким образом, выражение (6.6) можно переписать в виде

Подставляя выражение (6.6) для касательного напряжения в уравнение (6.3), будем иметь

Отсюда получим формулу для относительного угла закручивания круглого вала:

где произведение GI_ρ называют жёсткостью сечения при кручении;

I_ρ – полярный момент инерции сечения, который является геометрической характеристикой жёсткости круглого вала при кручении.

Для определения взаимного угла закручивания двух сечений, расположенных на расстоянии l, воспользуемся соотношением (6.7), из которого, интегрируя обе части равенства, найдём

В частном случае при M_к = const, GI_ρ = const получим

Для определения касательного напряжения в любой точке сечения достаточно в формулу (6.6) подставить выражение для θ по формуле (6.7). Тогда

Максимальное касательное напряжение, действующее на периферии сечения вала

где — полярный момент сопротивления сечения, который является геометрической характеристикой прочности круглого вала при кручении.

РАСЧЕТЫ НА ПРОЧНОСТЬ И ЖЕСТКОСТЬ ПРИ КРУЧЕНИИ

Обеспечение прочности при кручении элементов строительных конструкций круглого сечения производится по методу предельных состояний на основе условия

где R_ср – расчётное сопротивление материала стержня на срез. Для пластичных материалов принимают R_ср » 0,58R.

Помимо условий прочности должны соблюдаться и условия жёсткости, которые формулируются в отношении относительного угла закручивания в виде

где _расч – расчётный относительный угол закручивания, величина которого задаётся техническими условиями в зависимости от назначения вала.

При проектировочном расчёте из двух диаметров вала, полученных из условия прочности (6.12) и условия жёсткости (6.13), принимается большее значение.

СРАВНИТЕЛЬНАЯ ОЦЕНКА ВАЛОВ КРУГЛОГО И КОЛЬЦЕВОГО ПОПЕРЕЧНЫХ СЕЧЕНИЙ

Из эпюры касательных напряжений (см. рис.6.8) видно, что, удаляя материал вблизи оси вала, его прочность снижают весьма незначительно, так как эта часть материала для сплошного вала является малонагруженной. При равных площадях сечения, а следовательно, при одинаковой массе валов кольцевое сечение обладает большими полярными моментами инерции I_ρ и сопротивления W_ρ, чем сплошное, т.е. вал кольцевого сечения оказывается жёстче и прочнее. Наконец, при равной прочности или равной жёсткости, т.е. при одинаковых значениях W_ρ и I_ρ, полый вал получается легче сплошного.

КРУЧЕНИЕ ВАЛОВ НЕКРУГЛОГО СЕЧЕНИЯ

В инженерной практике довольно часто кручению подвергаются стержни, имеющие не круглое, а прямоугольное, треугольное, эллиптическое и другие сечения. В этих случаях гипотеза плоских сечений неприменима, так как сечения искривляются (депланируют). Коробление поперечных сечений, получающееся в результате того, что отдельные их точки при деформации смещаются вдоль оси стержня, называется депланацией.

Это обстоятельство не позволяет применить методы сопротивления материалов для решения задачи о напряжениях и перемещениях при кручении некруглых валов.

Для целого ряда сечений эта задача решена методами теории упругости. Приведём здесь некоторые окончательные результаты. Отметим, что в валах произвольного сечения, как и в круглых, касательные напряжения при кручении направлены по касательной к контуру.

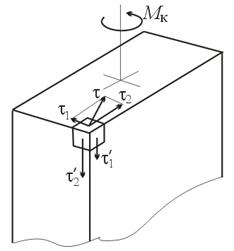
Если поперечное сечение имеет внешние углы, то в них касательные напряжения отсутствуют. Действительно, раскладывая напряжение τ вблизи угла, как показано на рис.6.10, на две составляющие по нормалям к сторонам угла, получаем напряжения τ₁ и τ₂. По закону парности на свободной поверхности вала должны возникнуть касательные напряжения τ ′ ₁ = τ₁ и τ ′‌ ₂ = τ₂. Но внешняя поверхность свободна от нагрузки. Таким образом, τ ′ ₁ = τ ′‌ ₂ = 0. Следовательно, вблизи внешнего угла касательные напряжения в поперечном сечении обращаются в нуль.

Наибольшие касательные напряжения, относительные и полные углы закручивания определяют по формулам

Здесь I_к и W_к – некоторые геометрические характеристики, которые условно называют моментом инерции и моментом сопротивления при кручении.

Наиболее часто встречаются валы прямоугольного сечения. В этом случае эпюры касательных напряжений имеют вид, показанный на рис. 6.11. Наибольшие напряжения возникают у поверхности посередине длинных сторон прямоугольника (в точках С и D), и определяются по формуле (6.14), где

Здесь h – длинная сторона прямоугольника;

Напряжения, возникающие у поверхности посредине коротких сторон (в точках А и B), меньше и выражаются через τ_max следующим образом:

Для определения углов закручивания в формулах (6.15) и (6.16) принимают

Коэффициенты a, b и g, зависящие от отношения h/b, приведены в справочных таблицах [6] на стр.8.

Отметим, что прочность и жёсткость прямоугольного вала значительно ниже, чем круглого с равновеликой площадью сечения. Эта разница возрастает с увеличением отношения сторон прямоугольника.

источники:

https://evakuatorinfo.ru/uchastok-vala-ne-ispytyvayuschiy-kruchenie-eto