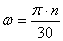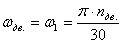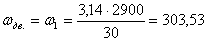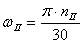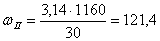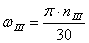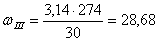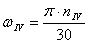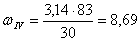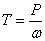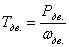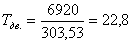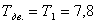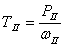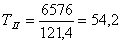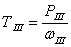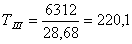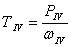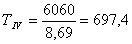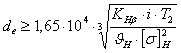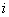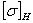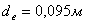Угловая скорость вращения вала радиусом (2 видео)

Угловую скорость каждого вала определяем по формуле

2. Угловую скорость каждого вала определяем по формуле

, с -1 (1.5)

где n –число оборотов на соответственном валу, об/мин.

Угловая скорость на I валу равна

с -1

Угловая скорость на II валу равна

с -1

Угловая скорость на III валу равна

с -1

Угловая скорость на IV валу равна

с -1

3. Крутящий момент на валах определяем по формуле

, Н·м (1.6)

где Р – мощность соответствующего вала, кВт

ω- угловая скорость соответствующего вала, с -1 .

, Н·м

Н·м

Крутящий момент на I валу равен

Н·м

Крутящий момент на II валу равен

, Н·м

Н·м

Крутящий момент на III валу равен

, Н·м

Н·м

Крутящий момент на IV валу равен

, Н·м

Н·м

Все расчеты для удобства записываем в сводную таблицу

Таблица 1.1. – силовые и скоростные параметры привода

Р в приводе уменьшилось не значительно из-за потерь в подшипниках. Число оборотов и угловая скорость в приводе сильно уменьшились из-за больших передаточных отношений.

2 Расчет конической передачи 2.1 Задача

Провести проектный расчет, подобрать материал, определить основные геометрические параметры и проверить на контакт.

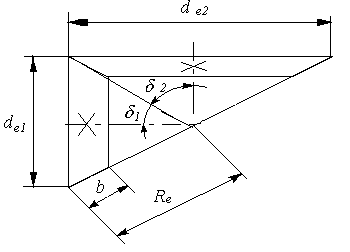
2.2 Расчетная схема

Рисунок 2.1 – Расчетная схема зацепления колес конической передачи

Данные для расчета передачи берем из кинематического расчета.

Таблица 2.1 — силовые и скоростные параметры для расчета промежуточной передачи

2.4 Условие расчета

Проектный расчет ведем на контакт, так как основной вид разрушения закрытых зубчатых передач — поверхностное выкрашивание зубьев в зоне контакта. Проверяем на контакт и изгиб.

2.5 Выбор материала и расчет допускаемых напряжений

Материалы для изготовления конических зубчатых колес подбирают по таблице 3.3 [1]).Для повышения механических характеристик материалы колес подвергают термической обработке. В зависимости от условий эксплуатации и требований к габаритным размерам передачи принимаем следующие материалы и варианты термической обработки (Т.О.).

Примем для колеса и шестерни сталь 40ХН и вариант термообработки ( таблица 3.3 [1]);

колесо—улучшение и закалка ТВЧ по контуру, НRC 48…53;

шестерня—улучшение и закалка ТВЧ по контуру, НRC 48…53.

Определяем допускаемые контактные напряжения и напряжения изгиба отдельно для колеса [σ]_н2 и [σ]_F₂ и шестерни [σ]_н1 и [σ]_F₁ по формулам (с.10 [2])

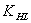
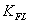
[σ]_н=·[σ]_н0 ; [σ]_F=·[σ]_F0

где — коэффициент долговечности при расчете по контактным напряжениям, так как редуктор рассчитан на долгий срок службы, то =1 (с.11 [2])

— коэффициент долговечности при расчете по изгибу , так как редуктор рассчитан на долгий срок службы, то =1 (с.11 [2]).

Определяем среднюю твердость зубьев колес НRC_ср=0,5(48+53)=50,5 Мпа

По таблице 2.2 [2] находим формулу для определения допускаемого контактного напряжения

2.6 Проектный расчет передачи 1. Определяем внешний делительный диаметр окружности колеса по формуле (с. 19 [2]) :

Читайте также: Стандартный диаметр вала гост

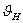
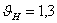
где — коэффициент вида конических колес, (с. 20 [2]) ;

— передаточное число быстроходной передачи;

Т₂ — вращающий момент на 1 промежуточном валу, Н·м;

— коэффициент неравномерности нагрузки по длине зуба. Для прирабатывающихся зубьев = 1,45 (таблица 2.3 [2]);

— допускаемое контактное напряжение колеса с менее прочным зубом или среднее допускаемое контактное напряжение, н/мм 2 .

Полученное значение внешнего делительного диаметра колеса округляем до ближайшего стандартного значения .

Содержание

Частота вращения: формула
Номинальная скорость вращения
Угловая скорость
Угловая скорость в конкретных случаях
Как определить угловую скорость
Угол поворота и период обращения
Циклическая частота вращения (обращения)
Переход от угловой к линейной скорости
Видео
Видео

Видео:Урок 44. Вращение твердого тела. Линейная и угловая скорость. Период и частота вращения.Скачать

Частота вращения: формула

Количество повторений каких-либо событий или их возникновения за одну единицу таймера называется частотой. Это физическая величина измеряется в герцах – Гц (Hz). Она обозначается буквами ν, f, F, и есть отношение количества повторяющихся событий к промежутку времени, в течение которого они произошли.

При обращении предмета вокруг своего центра можно говорить о такой физической величине, как частота вращения, формула:

N – количество оборотов вокруг оси или по окружности,
t – время, за которое они были совершены.

В системе СИ обозначается как – с-1 (s-1) и именуется как обороты в секунду (об/с). Применяют и другие единицы вращения. При описании вращения планет вокруг Солнца говорят об оборотах в часах. Юпитер делает одно вращение в 9,92 часа, тогда как Земля и Луна оборачиваются за 24 часа.

Видео:Вращательное движение. 10 класс.Скачать

Номинальная скорость вращения

Прежде, чем дать определение этому понятию, необходимо определиться, что такое номинальный режим работы какого-либо устройства. Это такой порядок работы устройства, при котором достигаются наибольшая эффективность и надёжность процесса на продолжении длительного времени. Исходя из этого, номинальная скорость вращения – количество оборотов в минуту при работе в номинальном режиме. Время, необходимое для одного оборота, составляет 1/v секунд. Оно называется периодом вращения T. Значит, связь между периодом обращения и частотой имеет вид:

К сведению. Частота вращения вала асинхронного двигателя – 3000 об./мин., это номинальная скорость вращения выходного хвостовика вала при номинальном режиме работы электродвигателя.

Как найти или узнать частоты вращений различных механизмов? Для этого применяется прибор, который называется тахометр.

Видео:Угловая скорость и радианная мера углаСкачать

Угловая скорость

Когда тело движется по окружности, то не все его точки движутся с одинаковой скоростью относительно оси вращения. Если взять лопасти обычного бытового вентилятора, которые вращаются вокруг вала, то точка расположенная ближе к валу имеет скорость вращения больше, чем отмеченная точка на краю лопасти. Это значит, у них разная линейная скорость вращения. В то же время угловая скорость у всех точек одинаковая.

Угловая скорость представляет собой изменение угла в единицу времени, а не расстояния. Обозначается буквой греческого алфавита – ω и имеет единицу измерения радиан в секунду (рад/с). Иными словами, угловая скорость – это вектор, привязанный к оси обращения предмета.

Формула для вычисления отношения между углом поворота и временным интервалом выглядит так:

ω – угловая скорость (рад./с);
∆ϕ – изменение угла отклонения при повороте (рад.);
∆t – время, затраченное на отклонение (с).

Читайте также: Размеры коленчатого вала мтз 80

Обозначение угловой скорости употребляется при изучении законов вращения. Оно употребляется при описании движения всех вращающихся тел.

Угловая скорость в конкретных случаях

На практике редко работают с величинами угловой скорости. Она нужна при конструкторских разработках вращающихся механизмов: редукторов, коробок передач и прочего.

Вычислить её, применяя формулу, можно. Для этого используют связь угловой скорости и частоты вращения.

π – число, равное 3,14;
ν – частота вращения, (об./мин.).

В качестве примера могут быть рассмотрены угловая скорость и частота вращения колёсного диска при движении мотоблока. Часто необходимо уменьшить или увеличить скорость механизма. Для этого применяют устройство в виде редуктора, при помощи которого понижают скорость вращения колёс. При максимальной скорости движения 10 км/ч колесо делает около 60 об./мин. После перевода минут в секунды это значение равно 1 об./с. После подстановки данных в формулу получится результат:

К сведению. Снижение угловой скорости часто требуется для того, чтобы увеличить крутящий момент или тяговое усилие механизмов.

Как определить угловую скорость

Принцип определения угловой скорости зависит от того, как происходит движение по окружности. Если равномерно, то употребляется формула:

Если нет, то придётся высчитывать значения мгновенной или средней угловой скорости.

Величина, о которой идёт разговор, векторная, и при определении её направления используют правило Максвелла. В просторечии – правило буравчика. Вектор скорости имеет одинаковое направление с поступательным перемещением винта, имеющего правую резьбу.

Рассмотрим на примере, как определить угловую скорость, зная, что угол поворота диска радиусом 0,5 м меняется по закону ϕ = 6*t:

Вектор ω меняется из-за поворота в пространстве оси вращения и при изменении значения модуля угловой скорости.

Видео:КРИВОЛИНЕЙНОЕ ДВИЖЕНИЕ - Угловое Перемещение, Угловая Скорость, Центростремительное УскорениеСкачать

Угол поворота и период обращения

Рассмотрим точку А на предмете, вращающимся вокруг своей оси. При обращении за какой-то период времени она изменит своё положение на линии окружности на определённый угол. Это угол поворота. Он измеряется в радианах, потому что за единицу берётся отрезок окружности, равный радиусу. Ещё одна величина измерения угла поворота – градус.

Когда в результате поворота точка А вернётся на своё прежнее место, значит, она совершила полный оборот. Если её движение повторится n-раз, то говорят о некотором количестве оборотов. Исходя из этого, можно рассматривать 1/2, 1/4 оборота и так далее. Яркий практический пример этому – путь, который проделывает фреза при фрезеровании детали, закреплённой в центре шпинделя станка.

Внимание! Угол поворота имеет направление. Оно отрицательное, когда вращение происходит по часовой стрелке и положительное при вращении против движения стрелки.

Если тело равномерно продвигается по окружности, можно говорить о постоянной угловой скорости при перемещении, ω = const.

В этом случае находят применения такие характеристики, как:

период обращения – T, это время, необходимое для полного оборота точки при круговом движении;
частота обращения – ν, это полное количество оборотов, которое совершает точка по круговой траектории за единичный временной интервал.

Читайте также: Сколько стоит замена компрессора холодильника от холодильник атлант

Интересно. По известным данным, Юпитер обращается вокруг Солнца за 12 лет. Когда Земля за это время делает вокруг Солнца почти 12 оборотов. Точное значение периода обращения круглого гиганта – 11,86 земных лет.

Видео:Нахождение отношения угловых точек лежащих на разных валах связанных не проскальзывающим ремнем #егэСкачать

Циклическая частота вращения (обращения)

Скалярная величина, измеряющая частоту вращательного движения, называется циклической частотой вращения. Это угловая частота, равная не самому вектору угловой скорости, а его модулю. Ещё её именуют радиальной или круговой частотой.

Циклическая частота вращения – это количество оборотов тела за 2*π секунды.

У электрических двигателей переменного тока это частота асинхронная. У них частота вращения ротора отстаёт от частоты вращения магнитного поля статора. Величина, определяющая это отставание, носит название скольжения – S. В процессе скольжения вал вращается, потому что в роторе возникает электроток. Скольжение допустимо до определённой величины, превышение которой приводит к перегреву асинхронной машины, и её обмотки могут сгореть.

Устройство этого типа двигателей отличается от устройства машин постоянного тока, где токопроводящая рамка вращается в поле постоянных магнитов. Большое количество рамок вместил в себя якорь, множество электромагнитов составили основу статора. В трёхфазных машинах переменного тока всё наоборот.

При работе асинхронного двигателя статор имеет вращающееся магнитное поле. Оно всегда зависит от параметров:

частоты питающей сети;
количества пар полюсов.

Скорость вращения ротора состоит в прямом соотношении со скоростью магнитного поля статора. Поле создаётся тремя обмотками, которые расположены под углом 120 градусов относительно друг друга.

Видео:Линейная и угловая скорости при равномерном движении по окружностиСкачать

Переход от угловой к линейной скорости

Существует различие между линейной скоростью точки и угловой скоростью. При сравнении величин в выражениях, описывающих правила вращения, можно увидеть общее между этими двумя понятиями. Любая точка В, принадлежащая окружности с радиусом R, совершает путь, равный 2*π*R. При этом она делает один оборот. Учитывая, что время, необходимое для этого, есть период Т, модульное значение линейной скорости точки В находится следующим действием:

Так как ω = 2*π*ν, то получается:

Следовательно, линейная скорость точки В тем больше, чем дальше от центра вращения находится точка.

К сведению. Если рассматривать в качестве такой точки города на широте Санкт-Петербурга, их линейная скорость относительно земной оси равна 233 м/с. Для объектов на экваторе – 465 м/с.

Числовое значение вектора ускорения точки В, движущейся равномерно, выражается через R и угловую скорость, таким образом:

а = ν2/ R, подставляя сюда ν = ω* R, получим: а = ν2/ R = ω2* R.

Это значит, чем больше радиус окружности, по которой движется точка В, тем больше значение её ускорения по модулю. Чем дальше расположена точка твердого тела от оси вращения, тем большее ускорение она имеет.

Поэтому можно вычислять ускорения, модули скоростей необходимых точек тел и их положений в любой момент времени.

Понимание и умение пользоваться расчётами и не путаться в определениях помогут на практике вычислениям линейной и угловой скоростей, а также свободно переходить при расчётах от одной величины к другой.

Видео:угловая и линейная скоростьСкачать