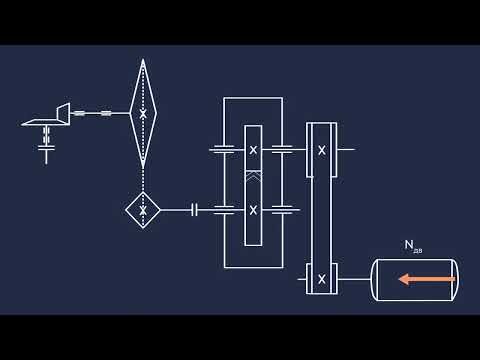
Все валы привода последовательно от вала двигателя обозначим римскими цифрами (Рис.1). Частоты вращения валов определяются последовательно от первого вала (вала электродвигателя) по формуле:
где ni+1 – частота вращения последующего вала;
ni – частота вращения предыдущего вала;
u – передаточное отношение передачи, стоящей между валами.
Угловые скорости валов определяются через частоты вращения валов по формуле
= 30 (13)
Применив формулы (12) и (13) к схеме привода получим выражения для определения частот вращения n (об/мин) и угловых скоростей валов ω (с -1 )
Фактическое значение частоты вращения приводного вала конвейера( ) может отличаться от расчетного. Допускаемое отклонение не более 3%.
Вращающие моменты на валах
Величины вращающих моментов на валах будут определяться нагрузкой на приводном валу барабана, т.е. величиной тягового усилия. Поэтому расчет вращающих моментов ведут от приводного вала к валу электродвигателя.
Вращающий момент на приводном валу барабана, Н . м
= ,(15)
Вращающие моменты на валах редуктора определяются последовательно от вала к валу по зависимости
где Тi+1 и – вращающие моменты на последующем и предыдущем валах;
— КПД передачи, стоящей между валами.
Применив формулу (15) к схеме привода получим выражения для определения вращающих моментов
= ; = ; = ; = .(17)
Мощности на валах
Мощности на валах определяют для каждого вала двумя способами (допустимое расхождение не более 3%):
-последовательно через предыдущую мощность и КПД передачи
-через момент и угловую скорость вала
Расчет зубчатых передач
Исходными данными для расчета цилиндрической передачи являются данные из кинематического расчета:
— момент на шестерне, Н . м,
( ) — частота вращения шестерни (колеса), мин –1 ,
u- передаточное отношение передачи;
и данные из технического задания:
Kc и Kг — коэффициенты использования в течение суток и в течение года,
— режим нагружения или циклограмма нагрузок.
Проектный расчет закрытых зубчатых передач (работающих в масляной ванне) выполняют на выносливость по контактным напряжениям с проверкой на изгиб.
Выбор материалов
Зубчатые колеса редукторов в большинстве случаев изготовляют из сталей, подвергнутых термическому или химико-термическому упрочнению. Рекомендуется назначать твердость шестерни на несколько единиц HRC или 20…30 единиц НВ большей, чем твердость колеса.
Читайте также: Датчик коленчатого вала рено канго
Механические свойства сталей, применяемых для изготовления зубчатых колес, приведены в таблице 2.1.
- Угловая скорость.
- Формулы частоты вращения циклической. Определение частоты вращения вала
- Что такое вращение?
- Описывающие вращение физические величины
- Угловая частота, период и угловая скорость
- Линейная скорость вращения, частота и частота угловая
- Задача на определение циклической частоты вращения вала
- 🔍 Видео
Видео:угловая СКОРОСТЬ формула угловое УСКОРЕНИЕ 9 классСкачать
Угловая скорость.
Угловой скоростью называется величина, численно равная скорости точек, расположенных от оси на расстоянии единицы длины.
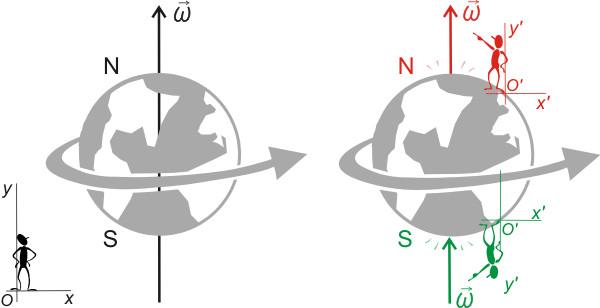
При вращении тела вокруг неподвижной оси АВ каждая точка тела М описывает окружность, перпендикулярную к оси, центр Р которой лежит на оси.
Скорость точки M направлена нормально к плоскости МАВ в сторону вращения. Равномерное вращение точки характеризуется постоянной угловой скоростью.
Угловой скоростью тела называют отношение угла поворота к интервалу времени, в течение которого совершен этот поворот. Если угловую скорость обозначить через w, то:
Угловая скорость выражается в радианах в секунду (рад/с).
При равномерном вращении, когда известна угловая скорость в начальный момент времени t0 = 0, можно определить угол поворота тела за время t и тем самым положение точек тела:
За один период (промежуток времени Т, в течение которого тело совершает один оборот по окружности) угол поворота φ равен 2π рад: 2π = wT, откуда:
Связь угловой скорости с периодом Т и частотой вращения ν выражается соотношением:
А связь между линейной и угловой скоростями определяется соотношением:
Видео:Карданная передача, основы. Карданные шарниры не равных и равных угловых скоростей (ШРУСы)Скачать
Формулы частоты вращения циклической. Определение частоты вращения вала
Одним из распространенных в природе и технике видов движения является вращение. Этот вид перемещения тел в пространстве характеризуется набором физических величин. Важная характеристика любого вращения — это частота. Формулу частоту вращения можно найти, зная определенные величины и параметры.
Видео:Урок 44. Вращение твердого тела. Линейная и угловая скорость. Период и частота вращения.Скачать
Что такое вращение?
Под ним в физике понимают такое перемещение материальной точки вокруг некоторой оси, при котором ее расстояние до этой оси остается постоянным. Оно называется радиусом вращения.
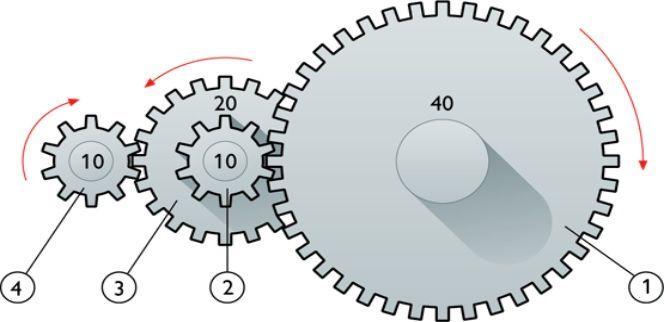
Примерами этого движения в природе является вращение планет вокруг Солнца и вокруг собственной оси. В технике вращение представлено движением валов, шестеренок, колеса автомобиля или велосипеда, перемещением лопастей ветровых мельниц.
Читайте также: Gaz bb13913 подшипник вторичного вала газель бизнес skf
Видео:6.2 Кинематический расчет приводаСкачать
Описывающие вращение физические величины
Для численного описания вращения в физике был введен ряд характеристик. Перечислим их и охарактеризуем.
В первую очередь это угол поворота, обозначается θ. Поскольку полная окружность характеризуется центральным углом в 2*pi радиан, то, зная величину θ, на которую повернулось вращающееся тело за определенный промежуток времени, можно определить число оборотов за это время. Кроме того, угол θ позволяет рассчитать линейный путь, пройденный телом вдоль кривой окружности. Соответствующие формулы для числа оборотов n и пройденного пути L имеют вид:
Где r — радиус окружности или радиус вращения.
Следующей характеристикой рассматриваемого типа движения является угловая скорость. Ее обычно обозначают буквой ω. Она измеряется в радианах в секунду, то есть показывает величину угла в радианах, на которые поворачивается вращающееся тело за одну секунду. Для угловой скорости в случае равномерного вращения справедлива формула:
Видео:Угловые скорости многозвенного механизмаСкачать
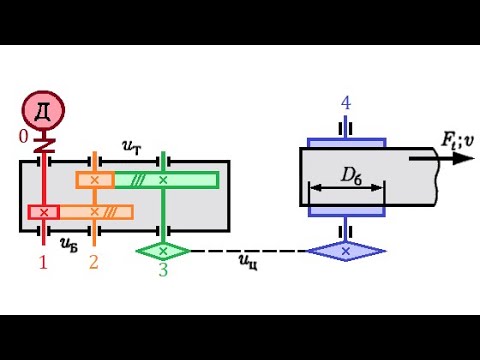
Угловая частота, период и угловая скорость
Выше уже отмечалось, что важным свойством любого вращательного движения является время, за которое совершается один оборот. Это время называется периодом вращения. Его обозначают буквой T и измеряют в секундах. Формулу для периода T можно записать через угловую скорость ω. Соответствующее выражение имеет вид:
Величина, обратная периоду, называется частотой. Ее измеряют в герцах (Гц). Для кругового движения удобно использовать не саму частоту, а ее угловой аналог. Обозначим ее f. Формула частоты вращения угловой f имеет вид:
Чтобы рассчитать угловую частоту, необходимо знать период вращательного движения.
Сравнивая две последние формулы, приходим к следующему равенству:
Это равенство означает следующее:
- формулы угловой частоты и угловой скорости совпадают, поэтому эти величины равны численно между собой;
- так же как и скорость, частота показывает, на какой угол в радианах поворачивается тело за одну секунду.
Различие между этими величинами единственное: угловая частота является величиной скалярной, скорость же — это вектор.
Видео:угловая и линейная скоростьСкачать
Линейная скорость вращения, частота и частота угловая
В технике для некоторых вращающих конструкций, например, шестерен и валов, известны их рабочие частоты μ и линейные скорости v. Тем не менее каждую из этих характеристик можно использовать для определения угловой или циклической частоты.
Читайте также: Замена крестовины рулевого вала тойота авенсис 1997 2003
Выше отмечалось, что частота μ измеряется в герцах. Она показывает количество оборотов вращающегося тела за одну секунду. Формула для нее принимает вид:
Если сравнить это выражение с соответствующим равенством для f, то формула, как найти частоту вращения f через μ описывающая, будет иметь вид:
Эта формула интуитивно понятна, поскольку μ показывает количество оборотов за единицу времени, а f отражает ту же самую величину, только представленную в радианах.
Линейная скорость v связана со скоростью угловой ω следующим равенством:
Поскольку модули величин f и ω равны, то из последнего выражения легко получить соответствующую формулу частоты вращения циклической. Запишем ее:
Где r — радиус вращения. Заметим, что скорость v линейно растет при увеличении радиуса r, при этом отношение этих величин является константой. Последнее умозаключение означает, что если измерять циклическую частоту вращения в любой точке сечения вращающегося массивного объекта, то она будет везде одинаковой.
Видео:Кинематика вращательного движения. ТермехСкачать
Задача на определение циклической частоты вращения вала
Угловые частоты вращения содержат полезную информацию, поскольку позволяют рассчитать такие важные физические характеристики, как момент импульса или угловую скорость. Решим такую задачу: известно, что рабочая частота вращения вала составляет 1500 оборотов в минуту. Чему равна циклическая частота для этого вала?
Из единиц измерения, приведенный в условии, понятно, что дана обычная частота μ. Поэтому формула частоты вращения вала циклической имеет вид:
Прежде чем ею пользоваться, следует перевести указанную в условии цифру к стандартным единицам измерения, то есть к обратным секундам. Поскольку вал за минуту делает 1500 оборотов, то за секунду он сделает в 60 раз меньше оборотов, то есть 25. То есть частота его вращения равна 25 Гц. Подставляя это число в записанную выше формулу, получаем значение циклической частоты: f = 157 рад/с.
- Свежие записи
- Чем отличается двухтактный мотор от четырехтактного
- Сколько масла заливать в редуктор мотоблока
- Какие моторы бывают у стиральных машин
- Какие валы отсутствуют в двухвальной кпп
- Как снять стопорную шайбу с вала
🔍 Видео
Вращательное движение. 10 класс.Скачать
Ременная передача. Урок №3Скачать
Вывод формулы угловой скоростиСкачать
Нахождение отношения угловых точек лежащих на разных валах связанных не проскальзывающим ремнем #егэСкачать
Мгновенный центр вращенияСкачать
Кинематический и силовой расчёт привода (общая методика расчёта). Ч.1Скачать
Как рассчитать диаметр шкивов и линейную скорость?Скачать
🔴 Курс ОГЭ-2024 по физике. Урок №5. Движение по окружности. Вращательное движение | Бегунов М.И.Скачать
Энкодеры. Подробный обзор с экспериментами!Скачать
Как устроен редуктор лодочного мотора , переключение передач вперед / назадСкачать
Как определить скорость вращения вала электродвигателя и его мощность.Скачать
Кинематический расчет привода ч 1Скачать
Угловой редуктор с реверсомСкачать
