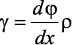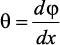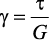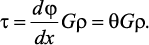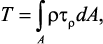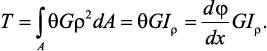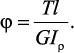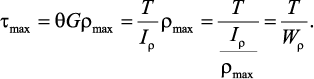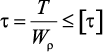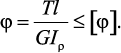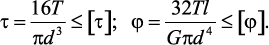Углы закручивания по длине вала

На этой странице приведен еще один пример решения задачи по Сопромату, в которой необходимо произвести расчет вала переменного сечения (ступенчатого), нагруженного крутящими моментами. По результатам расчетов необходимо подобрать размеры вала, а также определить максимальную деформацию вала на скручивание (угол закручивания).

Результаты расчетов оформлены эпюрами крутящих моментов, касательных напряжений и углов закручивания бруса.

Студентам технических специальностей ВУЗов в качестве методической помощи предлагаются к скачиванию готовые варианты контрольных работ по сопромату (прикладной механике). Представленные задания и примеры их решения предназначены, в частности, для учащихся Алтайского Государственного технического университета.
Варианты контрольных работ можно скачать в формате Word для ознакомления с порядком решения заданий, или для распечатывания и защиты (при совпадении вариантов).

Видео:Расчет вала на прочность и жесткость. Эпюра крутящих моментовСкачать

Расчет вала

Условие задачи:

К стальному валу, состоящему из 4-х участков длиной l₁…l₄ приложено четыре сосредоточенных момента М₁…М₄ (см. рис. 1 ).

Требуется:

Построить эпюру крутящих моментов М_кр , подобрать диаметр вала из расчета на прочность, построить эпюру максимальных касательных напряжений τ_max , построить эпюру углов закручивания φ вала и определить наибольший относительный угол закручивания вала.

Исходные данные:

Указания:

Вычертить схему вала в соответствии с исходными данными.
Знаки моментов в исходных данных означают: плюс – момент действует против часовой стрелки относительно оси Z , минус – по часовой стрелке (см. навстречу оси Z ). В дальнейшем значения моментов принимать по абсолютной величине.
Участки нумеровать от опоры.
Допускаемое касательное напряжение [ τ ] для стали принимать равным 100 МПа.

Решение:

1. Определим методом сечений значения крутящих моментов на каждом силовом участке от свободного конца вала.
Крутящий момент равен алгебраической сумме внешних моментов, действующих на вал по одну сторону сечения.

2. Подберем сечение вала из расчета на прочность при кручении по полярному моменту сопротивления для участка, где величина крутящего момента максимальная (без учета знака):

Так как для круглого сечения полярный момент равен: W_р = πD 3 /16 , то можно записать:

D ≥ 3 √ (16М_кр/π[τ]) ≥ 3√(16×12,2×10 3 /3,14×[100×10 6 ]) = 0,0855 м или D ≥ 85,5 мм.

( Здесь и далее знак «√» означает квадратный корень из выражения )

В соответствии со стандартным рядом, предусмотренным ГОСТ 12080-66, принимаем диаметр вала D = 90 мм.

3. Определим угол закручивания для каждого участка вала по формуле:

где
G – модуль упругости 2-го рода; для стали G = 8×10 10 Па;
I_p – полярный момент инерции (для круглого сечения I_р = πD 4 /32 ≈ 0,1D 4 , м 4 ).
Произведение G×I_р = 8×10 10 ×0,1×0,094 ≈ 524880 Н×м 2 – жесткость сечения данного вала при кручении.

Расчитываем углы закручивания на каждом участке:

4. Определяем углы закручивания сечений вала, начиная от жесткой заделки (опоры):

5. Определяем максимальное касательное напряжение на каждом силовом участке по формуле:

6. Наибольший относительный угол закручивания Θ_max определим по формуле:

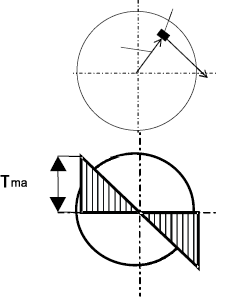
7. По результатам расчетов строим эпюры крутящих моментов М_кр , касательных напряжений τ_max и углов закручивания φ (см. рис. 2).

Видео:КРУЧЕНИЕ. ЭПЮРЫ ЗАКРУЧИВАНИЯ. Углы поворота. СопроматСкачать

Расчет валов на прочность и жесткость при кручении

Видео:КРУЧЕНИЕ ВАЛА. Касательные напряжения. Сопромат.Скачать

Расчет валов на прочность и жесткость при кручении

• Расчет вала на прочность И жесткость на кручение Для своей конструкции можно рекомендовать следующий порядок расчета вала на прочность и жесткость при кручении. По схеме вала и действующему на него крутящему моменту строится график

крутящего момента для отдельных участков (§ 16). Выберите материал расчетного вала и определите допустимое напряжение[t] для этого материала. Условия записи Секционная прочность 214 вала с максимальным значением крутящего момента(согласно диаграмме крутящего момента) (9.12).

Если вал достаточно длинный и отдельные секции достаточно сильно отличаются по величине крутящего Людмила Фирмаль

момента, то они должны быть ступенчато спроектированы. Диаметр вала каждой ступени рассчитывается по одной и той же формуле(9.12), но значения крутящего момента различны для разных участков в зависимости от графика крутящего момента. Учитывая, что можно написать формулу для расчета диаметра вала

из сплошного круглого вала Wp=уравнение (9.13: (9.16) Определить диаметр полой оси, заданный соотношением между размерами внутреннего и наружного диаметров из конструктивных соображений, т. е. коэффициент= — тогда, учитывая уравнение(9.11), из уравнения (9.13)следует:: (9.17)) После определения размеров вала из условий прочности проверьте жесткость вала по формуле (9.14).

• Допустимый относительный угол поворота вала составляет 0,3°для каждого метра статической нагрузки[0′] — длина вала, переменная нагрузка[0°1=0,25°, ударная нагрузка[0 ′ 4=0,15°]. Учитывая, что формула (9.14) представляет угол закрутки в радианах, значение данного допустимого угла преобразуется в радианы, и в испытании выполняется условие жесткости (9.14), в противном случае размеры вала должны выбираться из условия жесткости(9.15).): Подставляя в эту формулу формулу момента полярной инерции, находим ее для непрерывной оси (9.18) Для полого вала Иногда при расчете вала

известно, что передаваемая мощность n равна лошадиным силам, а число оборотов-n в минуту. В этом деле 21 крутящий момент формулы может быть выражен непосредственно в терминах мощности n и числа оборотов n, исходя из Формулы (3.1): МК=71 620-кгс*(9.20) мощность/(задается в киловаттах, когда крутящий момент определяется по формуле (3.2): МК-97 360-кгс * см.(9.21）) >

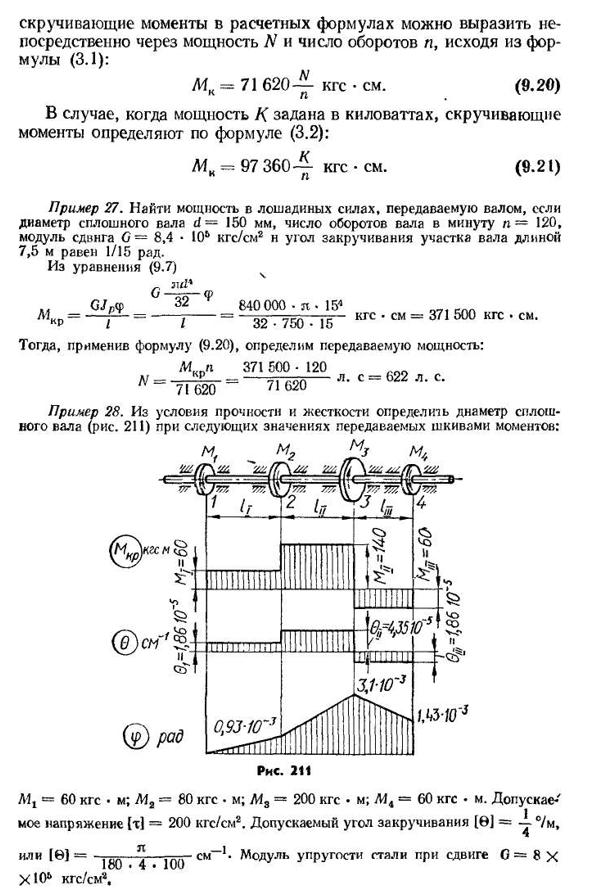
27, например. Найти мощность, передаваемую валом, диаметр Людмила Фирмаль

сплошного вала d-150мм, число оборотов вала n-120 в минуту, модуль сдвига G— 8,4 • 10 длина участка оси кгс / см2н с углом кручения 7,5 м составляет 1/15 Радиана. Из уравнения(9.7) И ой.. GJpat/7=/7 / =50 см h=J=90 см. В этом случае одна из секций фиксируется (рис. 211 настоящего раздела/). В пределах каждой секции 0-const угол кручения каждой секции изменяется по линейному закону,B, MD. Max=M V и формула на основе L\ymk В (А+Б) л[т] *

Читайте также: Что такое валы из песка

Видео:Кручение. Часть 6 Жесткость валаСкачать

Научная электронная библиотека

Лекция 7. КРУЧЕНИЕ

Крутящие моменты (внутренний силовой фактор) в поперечных сечениях стержня. Кручение стержней круглого поперечного сечения: допущения, деформации, напряжения, углы закручивания. Условия прочности, жёсткости. Построение эпюр крутящих моментов.

Кручение имеет место в случае действия на вал момента (пары сил) относительно его продольной оси, и в поперечных сечениях бруса возникает только один силовой фактор – крутящий момент. Брус, работающей на кручение называется валом. При кручении вала его поперечные сечения поворачиваются друг относительно друга, вращаясь вокруг оси бруса.

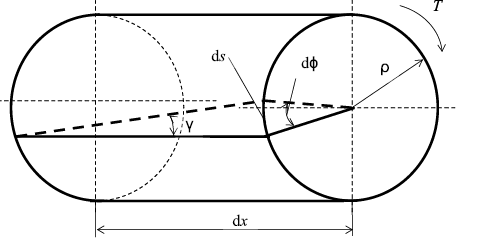
Напряжения и деформации при кручении бруса. Под действием внешнего скручивающего момента, приложенного на правом конце бруса, левый конец которого жестко закреплен, брус будет закручиваться. Выделим из бруса элементарный цилиндр длиной dx (рис. 19). Будем считать, что левое сечение бруса жестко закреплено. Под действием крутящего момента T правое сечение повернется на некоторый угол dφ.Так как ds = γ•dx = ρ•dφ, то получаем . Из данной зависимости видно, что угол сдвига γ изменяется по радиусу вала по линейному закону.

Рис. 19. Расчетная схема при кручении

Деформация бруса при кручении характеризуется относительным углом закручивания .

При малых углах закручивания вала в теории кручения круглых стержней принимаются допущения:

1. Поперечные сечения, плоские и перпендикулярные к его оси до деформации, остаются плоскими (не коробятся) и перпендикулярными к оси вала и после деформации (гипотеза Бернулли).

2. Радиусы поперечных сечений при деформации не искривляются и не изменяют своей длины.

3. Длина вала в результате закручивания не изменяется.

Поперечное сечение вала ведет себя при кручении, как жесткий диск, и деформацию кручения можно рассматривать, как результатсдвига одного поперечного сечения относительно другого. В этом случае в точках поперечного сечения вала возникают только касательные напряжения.

Теория кручения, основанная на упомянутых допущениях, подтверждается экспериментальными данными.

Согласно закону Гука при сдвиге, имеем . Откуда получаем:

Из полученной зависимости следует, что касательные напряжения изменяются по радиусу по линейному закону.

При кручении все внутренние силы, распределенные по поперечному сечению, приводятся к одной составляющей – к крутящему моменту. Касательные напряжения перпендикулярны радиусам, проведенные через точки их действия (рис. 20). Крутящий момент T в сечении бруса определяется по формуле

где ρ – плечо элементарной силы.

Подставляя значение касательного ускорения, получим

(8)

Элементарный угол закручивания бруса: 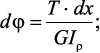полный угол закручивания

Максимальное касательное напряжение в поперечном сечении бруса будет определяться по зависимости:

Прочность и жесткость при кручении. Условие прочности при кручении имеет вид

(9)

Для бруса круглого сечения эти условия принимают вид:

Построение эпюр крутящих моментов. Крутящий момент, возникающий в поперечном сечении стержня, определяется методом сечений. Крутящий момент равен алгебраической сумме скручивающих моментов, приложенных к любой из частей стержня. Эпюра крутящих моментов – это график, показывающий изменения крутящего момента по длине вала. Правило знаков для эпюры крутящих моментов

При построении эпюры крутящих моментов используется правило знаков: скручивающий момент, вращающий рассматриваемую часть стержня против хода часовой стрелки при взгляде на поперечное сечение, вызывает в этом сечении положительный крутящий момент.

Брус разбивается на участке, на каждом участке проводится сечение и определяется крутящий момент. Затем строится эпюра крутящих моментов.

Видео:11. Кручение ( практический курс по сопромату )Скачать

ПроСопромат.ру

Видео:Кручение валаСкачать

Технический портал, посвященный Сопромату и истории его создания

Видео:Почему никто не знает об этой функции штангенциркуля?!Скачать

Архив рубрики: Задачи на кручение

Видео:Сопромат. Построение эпюр вала при кручении. Я в вк https://vk.com/id4682924Скачать

Проверочный и проектный расчеты при кручении

Задача. Для заданного стального бруса d=50мм (материал – сталь Ст3) построить эпюры крутящих моментов, углов поворота поперечных сечений. Проверить прочность бруса, если допускаемое касательное напряжение [τ]=30МПа. Подобрать для бруса кольцевое сечение при . Сравнить сечения по расходу материала.

1.Расставляем сечения на характерных участках. Начинаем расчет от свободного конца бруса, рассматривая правую часть и отбрасывая оставшуюся левую часть с заделкой. Каждое сечение рассматриваем отдельно, определяя в нем значение крутящего момента.

Строим эпюру М_К

2.Строим эпюру углов поворота сечений. Углы поворота сечений определяем по формуле

Расчет ведем по сечениям от неподвижного конца – стены А, в которой угол поворота равен нулю φ_А=0. В формуле обязательно следует учитывать знаки крутящих моментов.

Модуль сдвига для Ст3 G = 0,8·10 5 МПа = 0,8·10 8 кПа.

Определим полярный момент инерции для круглого сечения:

Вычисляем углы поворота сечений — от стены А.

Если требуется перейти к градусной мере, то:

Далее вычисляем все последующие углы поворота, учитывая ранее найденные:

Строим эпюру φ

3.Проверим прочность бруса по формуле

Максимальный крутящий момент с эпюры М_К = 0,75 кНм.

Определим полярный момент сопротивления сечения:

Тогда —прочность обеспечена.

4.Подбираем кольцевое сечение для вала с .

Наружный диаметр кольца определим по формуле проектного расчета для кольцевого сечения:

Тогда d = 0,8 · 60 = 48 мм.

Проверим прочность подобранного сечения. Полярный момент сопротивления для кольца:

5. Сравним варианты – круглое и кольцевое – по расходу материала

В задаче площадь круглого вала А = 19,6 см 2 , а у кольцевого сечения (полого) А = 10,7 см 2 , что позволяет говорить об экономии материала почти в два раза. Т.о. брус (вал) кольцевого сечения экономичнее равнопрочного сплошного.

Видео:Кручение. Расчет составного вала кольцевого сечения.Скачать

Задача на кручение

Для вала определить диаметр, построить эпюры крутящих моментов и углов закручивания.

1) Определяем величины внутренних крутящих моментов M. Для этого разбиваем стержень на участки (I, II, III, IV) и производим расчёт M со свободного конца стержня. Крутящий момент M в сечении равен алгебраической сумме моментов, действующих на стержень с одной стороны (справа) от рассматриваемого сечения.

Читайте также: Холодильники бош с не с китайским компрессором

Расчёт M соответственно по участкам IV, III, II, I:

Зная числовые значения крутящих моментов M, строится эпюра M, при этом положительные значения M откладываются вверх, а отрицательные – вниз от горизонтальной линии.

2) Определяем диаметр стержня из условия прочности: Выразим –полярный момент сопротивления при кручении круглого стержня через диаметр:тогда получим:

берётся из эпюры M по абсолютному значению. Диаметр стержня d округляется до большей величины.

3) Производим расчет жесткости вала при кручении, где — модуль сдвига, а (см 4 ) – полярный момент инерции сечения.

4) Производим расчет – углов закручивания концов участков стержня, начиная от закреплённого конца стержня, где ,(рад):Значения крутящих моментов на участках берутся из эпюры крутящих моментов с учётом их знака. Получив численные значения , строят эпюру . Примерная эпюра показана на рисунке.

Видео:Сопротивление материалов. Лекция: кручение круглого стержняСкачать

Задача

Ступенчатый стержень нагружен крутящим моментом Т .При каком отношении выполняется условие одинаковой прочности по всей длине стержня, если

Условие одинаковой прочности на участках будет выполнено в том случае ,если касательные напряжения будут одинаковы.

Определим касательные напряжения, обозначив крутящий момент в левой стене как , а в правой как :

Определим полярные моменты сопротивления сечений : Тогда найдем соотношение между и :

Теперь составим уравнение деформаций — углов поворота. Начнем от правой стены В, в которой . Внутренний крутящий момент во втором сечении будет равен , а крутящий момент в первом сечении будет равен . Тогда уравнение углов поворота: (2)

Полярные моменты инерции: Подставим эти значения в уравнение (2) и найдем соотношение между и :

Составим уравнение статики для заданной схемы:Тогда: (4)

Теперь, решая (4) , (3) и (1), получим отношение . Задача решена.

Видео:Основы работы в среде Solidworks Simulation. Кручение цилиндрического валаСкачать

Задача на расчет вала на прочность и жесткость при кручении

Для стального вала, нагруженного внешними крутящими моментами, построить эпюры внутренних крутящих моментов, определить размеры поперечного сечения в виде кольца (d/D=0,85) из условий прочности и жесткости, построить эпюры максимальных касательных напряжений, абсолютных и относительных углов поворота поперечных сечений.

Определим внутренние крутящие моменты. Расчет внутренних крутящих моментов проводится с помощью метода сечений.

Участок LK: М_L= М₄ = 5 кНм; М_К=М₄=5кНм.

Покажем эпюру крутящих моментов на рис.б.

Определяем размеры поперечного сечения вала из условия прочности и жесткости:, где полярный момент сопротивления сечения и полярный момент инерции сечения равны:Максимальный внутренний крутящий момент:

Тогда из условия прочности:

А из условия жесткости: Окончательно принимаем D=90мм.

Для подобранного сечения вала его геометрические характеристики:

Рассчитаем касательные напряжения для участков:

Построим эпюру касательных напряжений на рис.в.

Расчет относительных углов поворота на участках:

Сначала определим жесткость сечения вала при кручении:

Эпюра θ показана на рис. г.

Определение угловых перемещений характерных сечений (идем от опоры В, в которой угол поворота равен 0):

Эпюра φ представлена на рис.д.

Видео:Кручение. Построение эпюр крутящих моментов и углов закручивания.Скачать

Задача на температурные напряжения при кручении

Стальные стержни 1 и 2 нагреваются на . Площадь стержней А.

Определить максимальные напряжения.

При нагреве стержней на возникнут температурные напряжения.

Напряжения, вызванные изменением температуры в стержне постоянного сечения, не зависят от его длины, площади поперечного сечения, а зависят от модуля упругости, коэффициента линейного расширения и разности температур .

Эти напряжения создадут усилия:

Тогда крутящий момент:

Касательные напряжения:

Следует помнить, что при нагреве стержней в них возникают сжимающие напряжения, а при охлаждении – растягивающие. Эти напряжения, суммируясь с напряжениями от силовых факторов, могут значительно превышать допускаемые. Это обстоятельство следует учитывать при проектировании элементов конструкций.

Видео:Даже ОПЫТНЫЕ ВОДИТЕЛИ не знают ЭТИХ ПРАВИЛ - Круговое движение / Автоподставы / Повороты / АварийкаСкачать

Задача

К стальному валу приложены три известных момента:

Требуется: 1) установить, при каком значении Х угол поворота правого крайнего сечения вала равен нулю; 2) для найденного значения Х построить эпюру крутящих моментов; 3) при заданном значении [τ] определить диаметр вала из расчета на прочность и округлить его до ближайшей большей величины, соответственно равной 30, 35, 40, 45, 50, 60, 70, 80, 90, 100 мм; 4) построить эпюру углов поворота; 5) найти наибольший относительный угол закручивания (в градусах на 1м длины).

Решение: Обозначим границы участков русскими буквами А,……,Д.

I.Записываем условие, что угол поворота крайнего правого сечения (Д) вала равен нулю – исходя из условий задачи.

Данный угол поворота является суммой углов поворота вала на каждом участке:

Угол поворота на участке определяется по формуле:

, где М к — крутящий момент на данном участке, l — длина участка,

G — модуль сдвига , — для стали

— полярный момент инерции

Таким образом, , и с учетом условия задачи:

Так как вал имеет постоянное поперечное сечение, то

Определяем внутренние крутящие моменты на участках методом сечений. Идем от свободного конца вала, на каждом участке мысленно проводим сечение и рассматриваем равновесие всегда правой отсеченной части:

Подставляем найденные значения моментов в уравнение (1) :

2. Строим эпюру крутящих моментов. Для этого подставляем в выражения для моментов Мк найденные значения Х.

Полученные значения откладываем в виде ординат на эпюре

3.Определяем диаметр вала из условия прочности:

, где —максимальное касательное напряжение,

— максимальный крутящий момент (берется с эпюры Мкр по модулю),

— полярный момент сопротивления сечения

[τ]=80 МПа — допускаемое касательное напряжение

Определяем диаметр:

Принимаем диаметр вала d=45 мм=4,5 см

4. Построение эпюры углов поворота начинаем от опоры и строим нарастающим итогом. Предварительно посчитаем жесткость вала:

Угол поворота в левой опоре равен нулю, поскольку в заделке поворота быть не может:

В последней точке угол поворота должен получиться равным нулю (по условию задачи), таким он и получился. Строим эпюру углов поворота.

Читайте также: Ауди а4 приводные валы шруса

5. Наибольший относительный угол закручивания определим по формуле:

Полученный результат переведем в градусы на метр длины:

Видео:Как обойтись без динамометрического ключаСкачать

Статически неопределимые задачи при кручении. Задача2

Требуется: 1) Построить эпюру крутящих моментов и подобрать размеры поперечных сечений заданной формы, соблюдая следующие соотношения между ними:

2) Построить эпюру углов поворота.

Сначала составляем уравнение статики для всего бруса:

Здесь два неизвестных, следовательно, требуется еще одно уравнение. Его получим, если сформулируем условие совместности деформаций всех трех участков бруса. Оно заключается в том, что поворот правого опорного сечения относительно левого опорного сечения для рассматриваемого бруса невозможен, поскольку оба его концы жестко защемлены:

Сократим на , тогда будет:

Выразим моменты инерции сечений разных форм с учетом заданных соотношений размеров:

Итак, все моменты инерции выражены через один параметр с, что позволит довести до числа решение уравнения (2′):

или после сокращения на с 4 :

С помощью метода сечений выразим неизвестные крутящие моменты через один из реактивных опорных моментов, например, через М_А:

С учетом (а), (б) и (в) уравнение (2′′), будет:

откуда находим значение М_А:

Тогда из (а), (б) и (в) найдем:

Эти результаты показаны в виде эпюры крутящих моментов.

Подбор размеров сечений производится по условиям прочности:

— на первом участке

Для круглого сечения

При заданном соотношении d=c:

— на втором участке

Для кольцевого сечения

Здесь мы должны учесть соотношения размеров, при которых и найдены внутренние усилия, то – есть

— на третьем участке

Для прямоугольного сечения . При соотношениях

По таблице α=0,246. И тогда W_к=2∙0,246∙с 3 .

Из условия прочности

Из трех требуемых значений «с» (0,023м, 0,04м и 0,046м) принимаем наибольшее с=0,046м и тогда проектные значения размеров сечений на разных участках должны быть

— на первом участке: круглое сечение диаметром d=0,046м,

— на втором участке: кольцевое сечение с внутренним диаметром d=0,046м, а внешним у которого

— на третьем участке: прямоугольное сечение шириной b=c=0,046м

и высотой h=2b=2∙0,046=0,092 м,

у которого I_к=β∙h∙b 3 =0,229∙0,092∙0,046 3 =205∙10 -8 м 4 .

2. Построение эпюры углов поворота.

Для этого вычисляются углы поворота сечений, расположенных на границах участков бруса (эти сечения на схеме обозначены цифрами в кружочках), они откладываются в виде ординат, вершины которых соединяются прямыми линиями. Так:

α₀=0, поскольку крайнее левое сечение жестко защемлено и поворачиваться вокруг продольной оси z не может,

Равенство нулю угла поворота крайнего правого сечения, тоже жестко защемленного, служит контролем правильности всего решения задачи.

Видео:Что означают ЦИФРЫ на шляпке болта?Скачать

Статически неопределимые задачи при кручении. Задача1

Уравнение статики для всего бруса:

В этом уравнении два неизвестных (это реактивные моменты в опорах М_А и М_В). Следовательно, задача один раз статически неопределима, и для ее решения необходимо составить дополнительное уравнение, выражающее факт совместности деформаций всех участков бруса.

Здесь можно рассуждать следующим образом: если удалить одну из опор, то брус станет статически определимым

Теперь крайнее правое сечение получило возможность поворачиваться. Но в заданной системе этот поворот невозможен. Поэтому величину М_В в удаленной опоре следует подобрать так, чтобы угол поворота опорного сечения равнялся нулю:

α_В=0 – это условие деформации.

Раскрывая его, будем иметь:

Тогда условие совместности деформаций (а) превращается в уравнение совместности деформаций:

В этом уравнении три неизвестных крутящих момента (по количеству участков бруса). Для их определения выразим крутящие моменты через заданные внешние скручивающие моменты М₁, М₂ и реактивные моменты, используя метод сечений. Так в любом сечении первого участка:

((b)

Далее, в любом сечении второго участка

Наконец, в любом сечении третьего участка:

Подставляя (b), © и (d) в уравнение (2), будем иметь:

В этом уравнении содержится одно-единственное неизвестное: это реактивный момент в левой опоре М_А. Определив его из решения уравнения (2′), обратной подстановкой в формулы (b), © и (d) определим численные значения крутящих моментов , Таким образом статическая неопределимость задачи будет раскрыта.

Зная крутящие моменты, далее можно решить любую задачу прочности и жесткости бруса.

Видео:Как быстро рассчитать момент затяжки болтаСкачать

Кручение бруса тонкостенного замкнутого круглого сечения

Тонкостенное круглое сечение характеризуется средним радиусом R_ср и толщиной стенки трубы δ

Считается, что касательные напряжения по толщине стенки распределяются равномерно и равны:

Угол закручивания

Видео:Основы простого сопротивления. Часть 2. Кручение круглого валаСкачать

Кручение бруса прямоугольного сечения

Опыт показывает, что при кручении брусьев некруглого поперечного сечения сами сечения не остаются плоскими, то есть происходит депланация поперечных сечений. Исследовать напряженное и деформированное состояние таких брусьев при кручении методами сопротивления материалов не представляется возможным, так как в основе их лежит гипотеза плоских сечений (гипотеза Бернулли).

Задача о кручении бруса некруглого, в частности, прямоугольного сечения решена с помощью метода теории упругости, и на основе этого решения предложены простые расчетные формулы, имеющие ту же структуру, что и формулы для бруса круглого сечения, а именно:

Здесь: W_к=α∙h∙b 2 – момент сопротивления при кручении,

В этих формулах: b – меньшая из сторон прямоугольника,

h – большая сторона,

α, β – коэффициенты, значения которых приводятся в таблице в зависимости от отношения сторон h/b (эта таблица содержится в рубрике «Кручение», «Таблицы» или в любом учебнике сопротивления материалов).

Распределение касательных напряжений по прямоугольному сечению тоже отличается от распределения в круглом сечении:

Значения коэффициента γ Запись опубликована 05.09.2014 автором admin в рубрике Задачи, Задачи на кручение.

• Свежие записи
  • Чем отличается двухтактный мотор от четырехтактного
  • Сколько масла заливать в редуктор мотоблока
  • Какие моторы бывают у стиральных машин
  • Какие валы отсутствуют в двухвальной кпп
  • Как снять стопорную шайбу с вала

  
  

  источники:

  https://evakuatorinfo.ru/ugly-zakruchivaniya-po-dline-vala

  📹 Видео

  Как определить момент затягивания болта ГБЦ.Скачать

  

  Свободное кручение тонкостенного стержняСкачать

  

  Статически неопределимый вал. Расчет на прочность при крученииСкачать