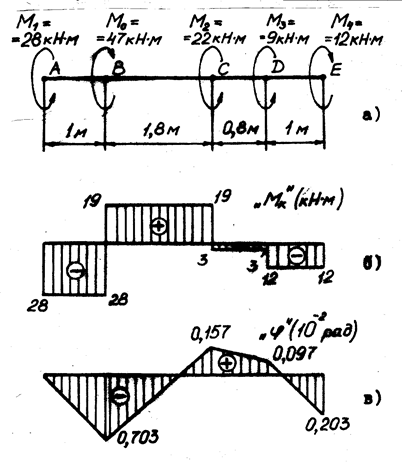
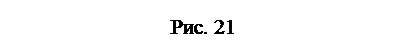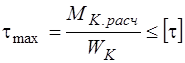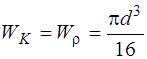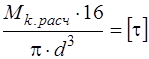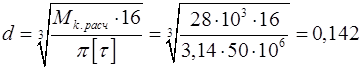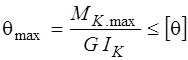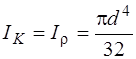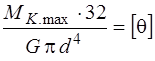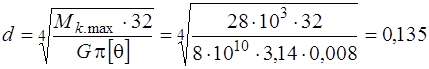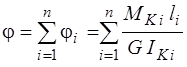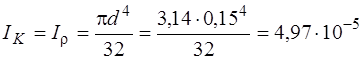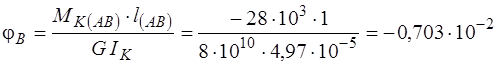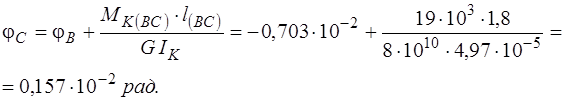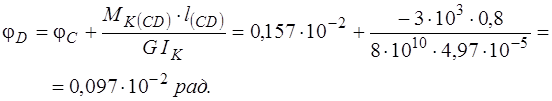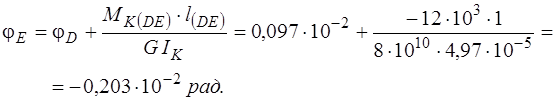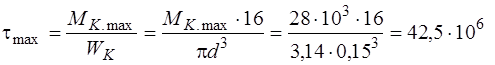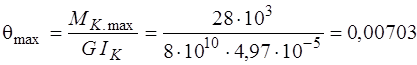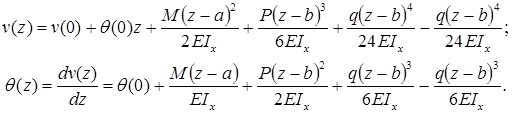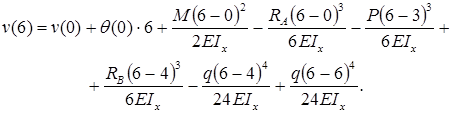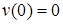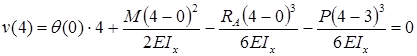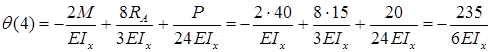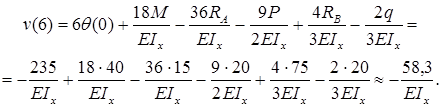1.Определяем величину и направление момента М0.
Вал под действием приложенных к нему моментов должен находится в равновесии, т.е. SМz = 0.
При записи этого уравнения моменты, направленные против часовой стрелки, считаем положительными, по часовой стрелке – отрицательными. Наблюдение ведем с правого конца вала.
SМz = — М4 + М3 + М2 + М0 + М1 = —12 + 9 + 22 + М0 +28 = 0,
Знак «минус» при М0 указывает на то, что этот момент в действительности направлен в направлении противоположном указанному на схеме задачи.
2. Изображаем расчетную схему вала (рис. 21а). Точки приложения моментов (границы участков) обозначаем буквами А , В , С , D , Е.
4. Определяем необходимый диаметр вала
,
.
Приравнивая выражение для tmax и [t] , получим:
м.
.
.
Приравнивая выражение для qmax и [q], получим:
,
м.
Из двух полученных значений d за ответ берём больший d = 0,142 м = = 142 мм. Округляем его до ближайшего большего стандартного значения d = 150 мм.
5. Строим эпюру углов закручивания (рис. 21в).
Углы поворота сечений будем определять относительно сечения А, т.к. угол поворота этого сечения равен нулю. Углы поворота других сечений (В, C, D, E) равны сумме углов закручивания участков вала, расположенных между сечением А и сечением, угол закручивания которого определяется:
.
Т.к. вал в этой задаче имеет один диаметр на всех участках, вычислим Ik
м 4 .
Угол поворота сечения В равен углу закручивания участка АВ:
рад.
Откладывая от нулевой линии полученные значения углов поворота сечений в масштабе с учётом знака, а затем, соединяя полученные точки прямыми линиями, получаем эпюру углов закручивания (рис. 21в).
6. Вычисляем наибольшее касательное напряжение наиболее нагруженном участке вала.
Наиболее нагруженным является участок АВ, т.к. здесь наибольший крутящий момент Мк(тах) = 28 кН×м.
Па =
7. Вычисляем наибольший относительный угол закручивания
рад/м.
Примечание. Iк был вычислен ранее (п. 5).
Видео:Кручение. Расчет составного вала кольцевого сечения.Скачать

Контрольная работа по сопромату
К стальному брусу круглого поперечного сечения приложены четыре крутящих момента , три из которых известны.
1) установить, при каком значении момента Х угол поворота правого концевого сечения равен нулю;
2) при найденном значении Х построить эпюру крутящих моментов;
3) при заданном значении допускаемого напряжения [ t ] определить диаметр вала из условия его прочности и округлить величину диаметра до ближайшей большей стандартной величины, равной 30, 35, 40, 45, 50, 60, 80, 90, 100 мм;
4) проверить, выполняется ли условие жесткости бруса при выбранном диаметре, если допускаемый угол закручивания 1 град/м;
5) построить эпюру углов закручивания.
Для всех вариантов принять модуль сдвига для стали
Числовые данные берутся из табл. 3, расчетные схемы — по рис. 6.
Числовые данные к задаче № 3
Рис. 6. Расчетные схемы к задаче № 3
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧИ № 3
Основные теоретические сведения и расчетные формулы
Брус, нагруженный парами сил, плоскости действия которых перпендикулярны его оси, испытывает деформацию кручения. Внутренним силовым фактором в поперечном сечении бруса в этом случае является крутящий момент , величину которого определяют методом сечений.
Читайте также: Замена подшипников первичного вала ваз 2112 16 клапанов
На основании этого метода можно сформулировать правило для определения крутящего момента в сечении бруса: крутящий момент в любом сечении бруса численно равен алгебраической сумме крутящих моментов, расположенных по одну сторону от этого сечения; при этом крутящий момент, приложенный к брусу, считается условно положительным, если при взгляде вдоль оси бруса с левого конца мы видим его направленным по ходу часовой стрелки.
Размеры и форма поперечного сечения бруса в расчетах на кручение учитываются двумя геометрическими характеристиками: полярным моментом инерции и полярным моментом сопротивления . Для круглого сечения они вычисляются по следующим формулам:
Крутящий момент вызывает в сечениях касательные напряжения , вычисляемых по формуле
где — крутящий момент в сечении бруса;
— полярный момент инерции сечения;
— расстояние от центра тяжести сечения до точки, в которой определяются напряжения.
Условие прочности записывается в виде
где — максимальная по модулю величина крутящего момента, определяемого по эпюре ;
— полярный момент сопротивления;
[ t ] — допускаемое касательное напряжение.
Деформация при кручении характеризуется углом закручивания j (рад):
где l — длина бруса;
G — модуль сдвига (модуль упругости второго рода).
Угол закручивания на единице длины бруса называется относительным углом закручивания и вычисляется по формуле
Условие жесткости накладывает ограничение на величину относительного угла закручивания:
где [ q ] — допускаемый угол закручивания.
Условие жесткости с учетом формулы (3.6) имеет вид
Рис. 7. Брус, работающий на кручение:
а — расчетная схема;
б — эпюра крутящих моментов;
в — эпюра углов закручивания
Для заданного бруса круглого сечения (рис. 7, а) определить величину момента X, при котором угол поворота свободного конца бруса равен нулю, построить эпюры крутящих моментов и углов закручивания, подобрать диаметр сечения по условию прочности и произвести проверку бруса на жесткость.
Числовые данные к задаче: а =0,8 м; в=1,0 м;
с=0,4 м; M1=2 кН × м; M2=0,9 кН × м; [ t ]=40 МПа; G=8 × 104 МПа.
1.Определение величины неизвестного крутящего момента Х.
Брус жестко заделан левым концом А, правый конец Е свободный. В сечениях В, С, и D приложены известные крутящие моменты. Для определения неизвестного момента Х используем условие равенства нулю угла поворота сечения Е.
Угол поворота сечения Е относительно сечения А определяется как сумма углов закручивания отдельных участков:
Крутящие моменты , входящие в выражение (3.8), определяются по приведенному выше правилу.
Вычисления начинаем с незакрепленного конца:
Используя выражения (3.9) и сокращая на , приводим уравнение (3.8) к виду
Подставляя значения a , b , c (рис. 7, а.) и решая это уравнение, получаем Х = 0,34 кН × м.
Примечание: если значение Х получится со знаком минус, направление крутящего момента задано неправильно. В данном примере X положителен, следовательно, направление крутящего момента, показанное на рис.7, правильно.
Читайте также: Сальник вала коробки передач правый
2. Построение эпюры крутящих моментов.
Найденное значение Х = 0,34 кН × м подставляем в выражения (3.9), вычисляя таким образом величину крутящего момента на каждом участке:
По найденным значениям строим эпюру крутящих моментов. Для этого рассматриваем последовательно участки ЕD, DC, CB и CA. Крутящие моменты, действующие на этих участках, уже вычислены.
Величина крутящего момента на каждом участке не зависит от положения сечения в пределах участка (крутящий момент постоянен), поэтому эпюра крутящих моментов ограничена отрезками прямых (рис.7,б). Построенная эпюра позволяет найти опасное сечение, т.е. такое, в котором действует максимальный (по модулю) крутящий момент.
В рассматриваемом примере опасными будут сечения в пределах участка АВ; расчетное значение крутящего момента
3. Подбор диаметра поперечного сечения бруса.
Используем условие прочности (3.4)
Учитывая, что , выразим диаметр из условия прочности
Подставляя 1,56 кН × м и , вычисляем диаметр поперечного сечения, округляя его до стандартной величины:
4. Проверка условия жесткости.
Условие жесткости записываем в форме (3.7):
По условию задачи [ q ]= 1 град/м. Переводя значение угла из градусной меры в радианную, получаем
Вычисляем выражение, стоящее в левой части условия жесткости, определив предварительно величину полярного момента инерции бруса:
Сравнение левой и правой частей условия жесткости показывает, что оно выполняется:
5. Построение эпюры углов закручивания.
Вычисляем углы закручивания по участкам, используя формулу (3.5):
Угол поворота каждого сечения равен сумме углов закручивания соответствующих участков бруса. Суммирование углов начинаем с незакрепленного конца А:
так как сечение в заделке неподвижно;
По вычисленным углам поворота сечений построена эпюра углов закручивания (рис. 7, в).
Равенство является проверкой решения, так как неизвестный крутящий момент Х определялся из условия равенства нулю угла поворота
Видео:Сопромат Тема №3 Задача №3.12 Угол поворота и прогиб сеченияСкачать

Универсальное уравнение оси изогнутой балки, вычисление прогибов и углов поворота поперечных сечений
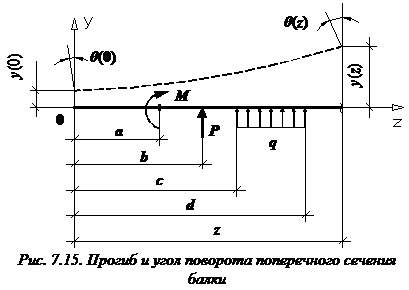
Определение прогибов и углов поворота поперечного сечения балки определяют с помощью универсального уравнения изогнутой оси балки (универсального уравнения упругой линии балки)
Формула (закон изменения) прогиба балки в сечении с координатой z и угол поворота сечения (рис. 7.15):
a и b – абсциссы точек приложения сосредоточенного момента M и сосредоточенной силы P, соответственно; c и d – координаты начала и конца участка, нагруженного распределенной нагрузкой.
В формулы входят только внешние усилия, которые расположены левее сечения, в котором определяются перемещения балки.
Если какая-нибудь нагрузка имеет противоположное указанному на рисунке 7.15 направление, то у соответствующих слагаемых в формулах прогибов и углов поворота сечений следует поменять знак на противоположный.
Прогиб 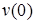
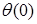
Видео:КРУЧЕНИЕ ВАЛА. Касательные напряжения. Сопромат.Скачать

Уравнение упругой линии балки на примере
Определим прогиб балки на консоли при 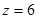
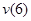
Прогиб балки в начале координат (на левой шарнирной опоре), равен нулю: .
Читайте также: Счетчик оборотов вала двигателя
Для определения угла поворота в начале координат необходимо составить дополнительное условие: прогиб на правой опоре равен нулю.
,
.
Знак «минус» говорит: прогиб балки на консоли происходит вниз. Число, стоящее в числителе, измеряется в килоньютонах на метр в кубе (кН·м3).
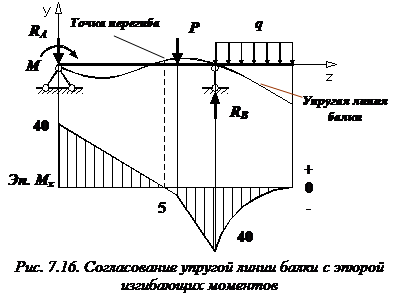
Примерный вид упругой линии балки показан на рис. 7.16.
Упругая линия балки должна быть согласована с эпюрой изгибающих моментов по дифференциальным зависимостям. Точка перегиба находится под сечением балки, в котором изгибающий момент равен нулю, что следует из закона Гука при изгибе.
Видео:Кручение валаСкачать

ПроСопромат.ру
Видео:Задача 4.2.3 Интеграл Мора. Аналитический методСкачать

Технический портал, посвященный Сопромату и истории его создания
Видео:Статически неопределимый вал. Расчет на прочность при крученииСкачать

Задача
К стальному валу приложены три известных момента:
Требуется: 1) установить, при каком значении Х угол поворота правого крайнего сечения вала равен нулю; 2) для найденного значения Х построить эпюру крутящих моментов; 3) при заданном значении [τ] определить диаметр вала из расчета на прочность и округлить его до ближайшей большей величины, соответственно равной 30, 35, 40, 45, 50, 60, 70, 80, 90, 100 мм; 4) построить эпюру углов поворота; 5) найти наибольший относительный угол закручивания (в градусах на 1м длины).
Решение: Обозначим границы участков русскими буквами А,……,Д.
I.Записываем условие, что угол поворота крайнего правого сечения (Д) вала равен нулю – исходя из условий задачи.
Данный угол поворота является суммой углов поворота вала на каждом участке:
Угол поворота на участке определяется по формуле:
, где М к — крутящий момент на данном участке, l — длина участка,
G — модуль сдвига , — для стали

Таким образом, , и с учетом условия задачи:
Так как вал имеет постоянное поперечное сечение, то
Определяем внутренние крутящие моменты на участках методом сечений. Идем от свободного конца вала, на каждом участке мысленно проводим сечение и рассматриваем равновесие всегда правой отсеченной части:
Подставляем найденные значения моментов в уравнение (1) :
2. Строим эпюру крутящих моментов. Для этого подставляем в выражения для моментов Мк найденные значения Х.
Полученные значения откладываем в виде ординат на эпюре
3.Определяем диаметр вала из условия прочности:


— максимальный крутящий момент (берется с эпюры Мкр по модулю),
— полярный момент сопротивления сечения
[τ]=80 МПа — допускаемое касательное напряжение
Определяем диаметр:
Принимаем диаметр вала d=45 мм=4,5 см
4. Построение эпюры углов поворота начинаем от опоры и строим нарастающим итогом. Предварительно посчитаем жесткость вала:
Угол поворота в левой опоре равен нулю, поскольку в заделке поворота быть не может:
В последней точке угол поворота должен получиться равным нулю (по условию задачи), таким он и получился. Строим эпюру углов поворота.
5. Наибольший относительный угол закручивания определим по формуле:

- Свежие записи
- Чем отличается двухтактный мотор от четырехтактного
- Сколько масла заливать в редуктор мотоблока
- Какие моторы бывают у стиральных машин
- Какие валы отсутствуют в двухвальной кпп
- Как снять стопорную шайбу с вала
🎥 Видео
КРУЧЕНИЕ. ЭПЮРЫ ЗАКРУЧИВАНИЯ. Углы поворота. СопроматСкачать
Кручение зажатого валаСкачать
Сопротивление материалов. Занятие 7. Расчет на прочность. Кручение стержняСкачать
Трехшарнирная рама. Расчет рамы на температурные воздействия. Нахождение угла поворота сечения КСкачать
Изгиб с кручениемСкачать
Сопротивление материалов. Лекция: кручение сплошного стержня некруглого сеченияСкачать
Кручение. Часть 6 Жесткость валаСкачать
2 1 Кручение круглого вала К выполнению РГЗСкачать
Сопротивление материалов. Лекция: кручение круглого стержняСкачать
Сопромат. Практическое занятие №1.4Скачать
Определение перемещений в балке. Метод сил. Правило Верещагина. СопроматСкачать
Сопромат Тема №3 Задача №3.9 Расчёт на жёсткостьСкачать
9.1 Расчет валов приводаСкачать
ANSYS Сопротивление материалов. D-05 (кручение, депланации).Скачать