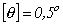Исследование отдельных участков и слоев цилиндрического бруса, нагруженного скручивающим (вращающим) моментом, дает основание полагать, что в поперечных сечениях этого бруса нормальные напряжения (направленные вдоль оси) отсутствуют, а возникают только касательные напряжения, модули которых расположены в плоскости исследуемого сечения.
Этот вывод опирается и на гипотезу о не надавливании волокон, предполагающую, что если брус представить в виде многочисленных цилиндрических продольных волокон, то при деформациях разного рода эти волокна не оказывают друг на друга силового воздействия (не давят друг на друга).
Как показали многочисленные опыты и исследования, эта гипотеза справедлива в определенном интервале деформаций, и погрешностями в расчетах, связанными с ее применением, можно пренебречь.
На рис. 1 видно, что абсолютный сдвиг сечения волокна а равен дуге аа1 , а сечения волокна b — дуге bb1 . Этот сдвиг (т. е. длины дуг) можно определить, зная угол φ закручивания исследуемого сечения относительно центральной оси:
дуга аа1 = rφ ; дуга bb1 = Rφ ,
где: r — расстояние от волокна а до оси кручения, R — радиус сечения круглого бруса, φ — полный угол закручивания бруса.
Так как радиусы сечений при кручении бруса остаются прямыми (принятое предположение), то величина абсолютного сдвига сечения волокон прямо пропорциональна их расстоянию от оси кручения, т. е. чем дальше от оси расположено продольное волокно, тем сильнее сдвинется его сечение относительно центральной оси.
Относительный сдвиг сечения произвольного продольного волокна b может быть определен по формуле:
γр = rφ / l ,
где φ / l = φ0 — относительный угол закручивания (для любого сечения круглого однородного бруса эта величина является постоянной). Тогда:
γр = φ0r .
Поскольку мы пришли к выводу, что при кручении в поперечных сечениях бруса возникает только деформация сдвига, то можно применить формулу, описывающую закон Гука при сдвиге:
Здесь τr — касательное напряжение в сечении волокна, G — коэффициент пропорциональности между относительным углом закручивания и величиной касательного напряжения, возникающего в сечении волокна, который называют модулем упругости второго рода .
Модуль упругости имеет такую же размерную единицу, как и напряжение (Па) и характеризует физические свойства материала бруса. Для разных материалов модуль упругости устанавливается опытно-экспериментальным путем и приводится в справочниках в виде таблиц, применяемых при расчетах.
На основании приведенной формулы Гука для сдвига при кручении можно сделать вывод, что для центрального волокна бруса (т. е. расположенного на оси закручивания в центре сечения) касательные напряжения равны нулю: если r = 0 , то τ = 0 .
Максимального значения касательные напряжения достигают в сечениях волокон, наиболее удаленных от оси закручивания бруса, т. е. на внешней поверхности бруса: если r = R , то τ = τmax .
Так как касательные напряжения в сечениях волокон бруса находятся в прямо пропорциональной зависимости от расстояния до оси кручения, то эпюра распределения напряжений вдоль радиуса сечения имеет вид треугольника (рис. 4) .
Исходя из схемы распределения напряжений, можно сделать вывод, что в круглых валах наиболее напряженными являются внешние слои, а внутренние почти не испытывают нагрузки. По этой причине многие валы машин и механизмов изготавливаются трубчатой формы (пустотелыми), что позволяет сэкономить дорогостоящий металл при незначительной потере прочности конструкции.
Если брус имеет по всей длине одинаковый диаметр (все сечения одинаковы по размерам и форме), и к каждому сечению приложен одинаковый крутящий момент, то касательные напряжения в каждом продольном волокне этого бруса будут одинаковы по величине.
Читайте также: Как добраться до крымского вала в москве
Определение угла закручивания и напряжений
Чтобы вывести формулы, определяющие угол закручивания и напряжения в поперечных сечениях бруса, рассечем его на расстоянии l1 от заделки ( рис. 1 ), и рассмотрим полученное сечение ( рис. 4 ).
Выделим в сечении бесконечно малую площадку dS на расстоянии r от оси кручения. Сила dQ , действующая на эту площадку, перпендикулярна радиусу r и может быть определена по формуле:
Интегрированием определим крутящий момент (момент внутренних сил), возникающих в этой площадке, относительно оси кручения бруса:
где Ir — полярный момент инерции сечения (для круглого бруса Ir = πD 4 / 32 = 0,1D 4 ).
Из полученной зависимости найдем относительный угол закручивания : φ0 = Мкр / (GIr) .
Полный угол закручивания сечения φ (рад) цилиндрического участка бруса длиной l может быть определен по формуле: φ = Мкрl / (GIr) .
Произведение модуля упругости G на полярный момент инерции сечения Ir называют жесткостью сечения .
Итак, можно сделать вывод, что полный угол закручивания круглого цилиндра прямо пропорционален крутящему моменту, длине цилиндра и обратно пропорционален жесткости сечения при кручении. Следует оговориться, что эта зависимость справедлива лишь до определенного предела, когда нагрузка и деформация пропорциональны.
Если цилиндрический брус (вал) состоит из нескольких участков, имеющих разный диаметр сечений (ступенчатый вал) или изготовленных из разного материала (составной вал), то полный угол закручивания такого бруса может быть определен, как сумма углов закручивания каждого отдельного участка.
Выведем теперь формулу для определения напряжений, возникающих в сечениях цилиндрического бруса при кручении.
Как мы уже определили ранее, при r = R касательные напряжения достигают максимального значения:
где Wr = Ir / R — момент сопротивления сечения кручению (или полярный момент сопротивления).
Момент сопротивления кручению равен отношению полярного момента инерции к радиусу сечения. Единица измерения момента сопротивления кручению — м 3 .
Моменты сопротивления кручению круглых валов
В технических расчетах наиболее часто приходится иметь дело с круглыми или трубчатыми брусьями (валами), поэтому определим величину момента сопротивления кручению для круглого вала и для вала, имеющего кольцевое сечение (труба).
Wr = Ir / 0,5D = πD 4 / (32×0,5) = πD 3 / 16 или приближенно: Wr ≈ 0,2D 3 .
Для кольца имеющего наружный диаметр D и внутренний диаметр d :
Wr = Ir / 0,5D = π(D 4 — d 4 ) / (32×0,5D) = π(D 4 — d 4 ) / 16D или приближенно: Wr ≈ 0,2(D 4 — d 4 ) / D .
Из последней формулы видно, что если полярный момент инерции кольцевого сечения можно определить, как разность между осевыми моментами инерции большого и малого кругов, то момент сопротивления кручения кольцевого сечения подобным образом рассчитать нельзя.
Итак, для определения напряжений в сечениях круглого бруса следует использовать формулы:
для сплошного вала: τmax ≈ Мкр / 0,2D 3
для трубчатого вала: τmax ≈ МкрD / (D 3 — d 3 )
Угол закручивания цилиндрического вала: φ = Мкрl / (GIr) .
Эти формулы применяют при решении задач и выполнении расчетов на прочность для скручиваемых валов.
Материалы раздела «Деформация кручения»:
Видео:КРУЧЕНИЕ. ЭПЮРЫ ЗАКРУЧИВАНИЯ. Углы поворота. СопроматСкачать
Определение угла закручивания при кручении круглого вала.
Угол закручивания, приходящийся на единицу длины, называют относительным углом закручивания
Читайте также: Бензиновые моторы с вертикальным валом
.
Для обеспечения требуемой жесткости вала необходимо, чтобы наибольший относительный угол закручивания не превосходил допускаемого:
.
Эта формула выражает условие жесткости вала при кручении. Обычно принимается на 1 м длины вала.
Условие жесткости при кручении и решении задач СМ на его основе. Рациональные формы сечений валов при кручении. Рациональная форма сечения вала
38 вопрос выражает условие жесткости, но как описать 3 задачи СМ я не представляю. По своей сути это нахождения нагрузок, моментов и т.д. Анализируя эпюру касательных напряжений можно отметить, что наибольшие напряжения возникают на поверхности вала, в центральной части они значительно меньше и на продольной оси равны нулю. Следовательно, в сплошном валу материал, находящийся в центральной части в значительной степени недогружен, его вклад в прочность вала мал. Поэтому рациональным для валов считается кольцевое сечение.
Изгиб. Закон распределения нормальных напряжений по высоте поперечного сечения
Изгибом называется вид нагружения бруса, при котором к нему прикладывается момент, лежащий в плоскости проходящей через продольную ось. В поперечных сечениях бруса возникают изгибающие моменты. При изгибе возникают деформация, при которой происходит искривление оси прямого бруса или изменение кривизны кривого бруса.
Брус, работающий при изгибе, называется балкой. Конструкция, состоящая из нескольких изгибаемых стержней, соединенных между собой чаще всего под углом 90°, называется рамой.
Изгиб называется плоским или прямым, если плоскость действия нагрузки проходит через главную центральную ось инерции сечения (рис.6.1).
При плоском поперечном изгибе в балке возникают два вида внутренних усилий: поперечная сила Q и изгибающий момент M. В раме при плоском поперечном изгибе возникают три усилия: продольная N, поперечная Q силы и изгибающий момент M.
Если изгибающий момент 
является единственным внутренним силовым фактором, то такой изгиб называется чистым (рис.6.2). При наличии поперечной силы 
изгиб называется поперечным. Строго говоря, к простым видам сопротивления относится лишь чистый изгиб; поперечный изгиб относят к простым видам сопротивления условно, так как в большинстве случаев (для достаточно длинных балок) действием поперечной силы при расчетах на прочность можно пренебречь.
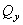
Косой изгиб — изгиб, при котором нагрузки действуют в одной плоскости, не совпадающей с главными плоскостями инерции.
Сложный изгиб — изгиб, при котором нагрузки действуют в различных (произвольных) плоскостях.
Закон распределения я не нашел.
Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.
Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ — конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой.
Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций.
Видео:Сопротивление материалов. Лекция: кручение круглого стержняСкачать
ПроСопромат.ру
Видео:КРУЧЕНИЕ ВАЛА. Касательные напряжения. Сопромат.Скачать
Технический портал, посвященный Сопромату и истории его создания
Видео:Кручение валаСкачать
Кручение
Внутренний крутящий момент в сечении вала Мк (может быть обозначен буквой Т, Мz) вычисляется с помощью метода сечений, при этом моменты учитываются по одну сторону от сечения.
где Мi – внешний активный или реактивный крутящий момент; правило знаков для внутренних крутящих моментов устанавливается произвольно.
Читайте также: Гайка вала кпп маз
Для вала с круглым (в т.ч. в виде кольца) поперечным сечением касательные напряжения определяются по формуле:
где — это полярные моменты инерции для сплошного и кольцевого сечений соответственно, ρ – координата произвольной точки сечения, D, d – наружний и внутренний диаметры сечения.
Максимальные касательные напряжения действуют в точках поверхностного слоя при ρ=ρmax
Условие прочности по допускаемым напряжениям
где — это допускаемое касательное напряжение.
Угол закручивания (рад) на силовом участке вала при постоянных значениях крутящего момента и поперечного момента инерции для данного участка вычисляется следующим образом
где G – модуль сдвига
Относительный угол закручивания (рад/м) для силового участка
Условие жесткости при кручении вала с круглым поперечным сечением записывается в виде
Для вала с прямоугольным поперечным сечением эпюры касательных напряжений имеют вид.
В характерных точках сечения
угол закручивания на силовом участке вала
где α, η, β – коэффициенты, зависящие от отношения a/b (или h/b — отношение большей стороны прямоугольника к меньшей)
Если вал с эллиптической формой поперечного сечения и полуосями a и b, то его характерные эпюры касательных напряжений будут выглядеть следующим образом.
Касательные напряжения в характерных точках сечения
Угол закручивания на силовом участке вала
Кручение бруса тонкостенного замкнутого круглого сечения
Тонкостенное круглое сечение характеризуется средним радиусом Rср и толщиной стенки трубы δ:
Считается, что касательные напряжения по толщине стенки распределяются равномерно и равны:
Угол закручивания
Кручение пустотелых валов круглого сечения
Трубчатое сечение бруса в условиях кручения оказывается наиболее рациональным, так как материал из центральной зоны сечения, слабо напряженной, удален в область наибольших касательных напряжений. Вследствие этого прочностные свойства материала используются значительно полнее, чем в брусьях сплошного круглого сечения, и при всех прочих равных условиях применение трубчатого сечения вместо сплошного позволяет экономить материал.
Теория расчета бруса сплошного круглого сечения полностью применима и к пустотелым валам. Изменяются лишь геометрические характеристики сечения:
Кручение бруса прямоугольного сечения
Опыт показывает, что при кручении брусьев некруглого поперечного сечения сами сечения не остаются плоскими, то есть происходит депланация поперечных сечений. Исследовать напряженное и деформированное состояние таких брусьев при кручении методами сопротивления материалов не представляется возможным, так как в основе их лежит гипотеза плоских сечений (гипотеза Бернулли).
Задача о кручении бруса некруглого, в частности, прямоугольного сечения решена с помощью метода теории упругости, и на основе этого решения предложены простые расчетные формулы, имеющие ту же структуру, что и формулы для бруса круглого сечения, а именно:
Здесь: Wк=α∙h∙b2– момент сопротивления при кручении,
Iк=β∙h∙b3 – момент инерции при кручении.
В этих формулах: b – меньшая из сторон прямоугольника,
h – большая сторона,
α, β – коэффициенты, значения которых приводятся в таблице в зависимости от отношения сторон h/b (эта таблица содержится в рубрике «Кручение» или в любом учебнике сопротивления материалов).
Распределение касательных напряжений по прямоугольному сечению тоже отличается от распределения в круглом сечении:
Значения коэффициента γ Запись опубликована 04.09.2014 автором admin в рубрике Кручение, Сопромат.
- Свежие записи
- Чем отличается двухтактный мотор от четырехтактного
- Сколько масла заливать в редуктор мотоблока
- Какие моторы бывают у стиральных машин
- Какие валы отсутствуют в двухвальной кпп
- Как снять стопорную шайбу с вала
📽️ Видео
Расчет вала на прочность и жесткость. Эпюра крутящих моментовСкачать
Кручение. Расчет составного вала кольцевого сечения.Скачать
11. Кручение ( практический курс по сопромату )Скачать
Основы простого сопротивления. Часть 2. Кручение круглого валаСкачать
2 1 Кручение круглого вала К выполнению РГЗСкачать
Кручение зажатого валаСкачать
Кручение. Часть 6 Жесткость валаСкачать
Кручение. Построение эпюр крутящих моментов и углов закручивания.Скачать
Сопромат. Построение эпюр вала при кручении. Я в вк https://vk.com/id4682924Скачать
Кручение круглого стержняСкачать
Основы сопромата. Задача 5. Расчет стержня на кручениеСкачать
Сопромат. Практическое занятие №1.4Скачать
Сопротивление материалов. D-06 (стержень круглого поперечного сечения закручен внешним моментом).Скачать
Статически неопределимый вал. Расчет на прочность при крученииСкачать
Сопротивление материалов. Лекция: кручение тонкостенного профиляСкачать
28. Статически неопределимый стержень ( кручение ) ( практический курс по сопромату )Скачать
