Видео:КРУЧЕНИЕ. ЭПЮРЫ ЗАКРУЧИВАНИЯ. Углы поворота. СопроматСкачать

Кручение
Внутренний крутящий момент в сечении вала Мк (может быть обозначен буквой Т, Мz) вычисляется с помощью метода сечений, при этом моменты учитываются по одну сторону от сечения.
где Мi – внешний активный или реактивный крутящий момент; правило знаков для внутренних крутящих моментов устанавливается произвольно.
Для вала с круглым (в т.ч. в виде кольца) поперечным сечением касательные напряжения определяются по формуле:
где — это полярные моменты инерции для сплошного и кольцевого сечений соответственно, ρ – координата произвольной точки сечения, D, d – наружний и внутренний диаметры сечения.
Максимальные касательные напряжения действуют в точках поверхностного слоя при ρ=ρmax
Условие прочности по допускаемым напряжениям
где — это допускаемое касательное напряжение.
Угол закручивания (рад) на силовом участке вала при постоянных значениях крутящего момента и поперечного момента инерции для данного участка вычисляется следующим образом
где G – модуль сдвига
Относительный угол закручивания (рад/м) для силового участка
Условие жесткости при кручении вала с круглым поперечным сечением записывается в виде
Для вала с прямоугольным поперечным сечением эпюры касательных напряжений имеют вид.
В характерных точках сечения
угол закручивания на силовом участке вала
где α, η, β – коэффициенты, зависящие от отношения a/b (или h/b — отношение большей стороны прямоугольника к меньшей)
Если вал с эллиптической формой поперечного сечения и полуосями a и b, то его характерные эпюры касательных напряжений будут выглядеть следующим образом.
Касательные напряжения в характерных точках сечения
Угол закручивания на силовом участке вала
Кручение бруса тонкостенного замкнутого круглого сечения
Тонкостенное круглое сечение характеризуется средним радиусом Rср и толщиной стенки трубы δ:
Считается, что касательные напряжения по толщине стенки распределяются равномерно и равны:
Угол закручивания
Кручение пустотелых валов круглого сечения
Трубчатое сечение бруса в условиях кручения оказывается наиболее рациональным, так как материал из центральной зоны сечения, слабо напряженной, удален в область наибольших касательных напряжений. Вследствие этого прочностные свойства материала используются значительно полнее, чем в брусьях сплошного круглого сечения, и при всех прочих равных условиях применение трубчатого сечения вместо сплошного позволяет экономить материал.
Теория расчета бруса сплошного круглого сечения полностью применима и к пустотелым валам. Изменяются лишь геометрические характеристики сечения:
Кручение бруса прямоугольного сечения
Опыт показывает, что при кручении брусьев некруглого поперечного сечения сами сечения не остаются плоскими, то есть происходит депланация поперечных сечений. Исследовать напряженное и деформированное состояние таких брусьев при кручении методами сопротивления материалов не представляется возможным, так как в основе их лежит гипотеза плоских сечений (гипотеза Бернулли).
Задача о кручении бруса некруглого, в частности, прямоугольного сечения решена с помощью метода теории упругости, и на основе этого решения предложены простые расчетные формулы, имеющие ту же структуру, что и формулы для бруса круглого сечения, а именно:
Читайте также: Подшипник первичного вала шкода рапид
Здесь: Wк=α∙h∙b2– момент сопротивления при кручении,
Iк=β∙h∙b3 – момент инерции при кручении.
В этих формулах: b – меньшая из сторон прямоугольника,
h – большая сторона,
α, β – коэффициенты, значения которых приводятся в таблице в зависимости от отношения сторон h/b (эта таблица содержится в рубрике «Кручение» или в любом учебнике сопротивления материалов).
Распределение касательных напряжений по прямоугольному сечению тоже отличается от распределения в круглом сечении:
Значения коэффициента γ Запись опубликована 04.09.2014 автором admin в рубрике Кручение, Сопромат.
Видео:Расчет вала на прочность и жесткость. Эпюра крутящих моментовСкачать

Электронная библиотека
Кручение — это такой вид деформации бруса, при котором в его поперечных сечениях возникает только один внутренний силовой фактор — крутящий момент (Мz).
Деформация кручения возникает при нагружении бруса парами сил, плоскости действия которых перпендикулярны его продольной оси Z. Эти пары сил будем называть скручивающими моментами.
Крутящий момент Mz в произвольном поперечном сечении численно равен алгебраической сумме внешних скручивающих моментов, приложенных к брусу по одну из сторон от сечения.
Знак крутящего момента не имеет физического смысла, но для определенности считается, что внешний скручивающий момент, направленный против часовой стрелки (если смотреть со стороны сечения), вызывает в данном сечении положительный крутящий момент. Если же внешний момент вращает отсеченную часть бруса по часовой стрелке (если смотреть со стороны сечения), то крутящий момент Mz в рассматриваемом поперечном сечении будет отрицательным.
В дальнейшем будем рассматривать только брус круглого поперечного сечения.
Касательные напряжения, возникающие в поперечных сечениях бруса, достигают наибольшего значения в точках контура поперечного сечения и равны:
где Wp=pd 3 /16 — полярный момент сопротивления бруса круглого поперечного сечения при кручении, м 3 . Здесь d — диаметр вала, м.
Угол закручивания (ji) участка вала постоянного поперечного сечения, на котором действует постоянный крутящий момент Mzi, определяется по следующей формуле:
где l — длина участка вала данного диаметра, на котором действует постоянный крутящий момент Mz, м; G — модуль упругости второго рода или модуль сдвига, Па; — полярный момент инерции.
Условие прочности при кручении записывается в следующем виде:
где [t] — допускаемое касательное напряжение, Па.
При проектном расчете формула (3.3) преобразовывается к виду
При определении угла закручивания всего вала необходимо просуммировать углы закручивания jI отдельных участков:
где n — число участков стержня.
Произведение GIp называется жесткостью сечения бруса круглого сечения при кручении.
Условие жесткости при кручении записывается в виде:
где j0 — относительный угол закручивания тела (угол закручивания на единицу длины), Н/м; [j0]- допускаемый относительный угол закручивания.
Исходные данные: G = 0,4 Е; Е = 2*105 МПа; Т1 = 6 кН*м; Т2 = 2 кН*м; Т3 = 1 кН*м; Т4 = 3 кН*м; а =1м; в = 0,5 м; с = 2 м; d =1,5 м; е = 1 м; t = 20 МПа.
Построить эпюру крутящих моментов, определить диаметр вала, проверить на прочность по касательным напряжениям, построить эпюру углов закручивания.
Читайте также: Максимальные напряжения для круглого вала
а) Построение эпюры крутящих моментов Mz
Внешние скручивающие моменты T1, T2 и T3 принимаем положительными, T4 — отрицательным (рис.3.3, а).
Определим значения крутящих моментов на отдельных участках:
По полученным результатам строим эпюру крутящих моментов Мz (рис.3.3, б).
б) Определение диаметров вала
Диаметры валов d1 и d2 определяются из условия прочности на кручение по формуле (3.4):
Полученные значения диаметров вала округляем до нормальных линейных размеров / 2 /: D1 = 120мм; d2 = 95мм.
в) Построение эпюры касательных напряжений по длине вала
Касательные напряжения определяем по формуле (3.3), предварительно определив полярные моменты сопротивления сечений вала:
По полученным результатам строим эпюру касательных напряжений t (рис. 3.3, в).
г) Построение эпюры углов закручивания
Углы закручивания j сечения вала относительно жесткой заделки найдем по формуле (3.5), предварительно определив полярные моменты инерции сечений:
По полученным результатам строим эпюру углов закручивания j (рис. 3.3, г).
Срочно?
Закажи у профессионала, через форму заявки
8 (800) 100-77-13 с 7.00 до 22.00
Видео:КРУЧЕНИЕ ВАЛА. Касательные напряжения. Сопромат.Скачать

Кручение
2.4.1. Общие сведения о деформации кручения
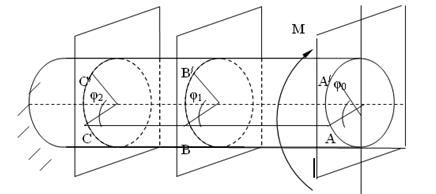
Наглядное представление о деформации кручения дает действие двух равных и противоположно направленных крутящих моментов (рис.2.20).
В результате деформации образующие вала получают вид винтовых линий. Такой вид получают образующие валы и в случае следующего закрепления (рис.2.21).
При действии крутящего момента М все линии рассматриваемой образующей будут отклоняться от первоначального положения на некоторые углы по окружности. На основе этого можно сделать выводы:
1. При кручении, в каждом сечении вала происходит поворот точек по окружности относительно оси. Следовательно, вал испытывает кручение, если к нему прикладывается пара сил направленных перпендикулярно осям.
2. Под действием внешних моментов, в поперечном сечении вала, возникает единственная составляющая главного момента, а именно крутящий момент Мк (рис. 2.22).
3. Деформация кручения вала заключается в повороте поперечных сечений относительно друг друга, при этом углы поворота прямопропорциональны растяжению.
4. Угол поворота рассматриваемого сечения равен углу закручивания части вала, которая заключена между данным сечением и заделкой. Угол кольцевого сечения называется углом закручивания вала.
5. В произвольном сечении угол поворота можно оценить относительным углом закручивания:
где — угол закручивания выделенного элемента; — расстояние от рассматриваемого сечения до заделки, — относительный угол закручивания.
Если балка длиной l м имеет постоянное поперечное сечение и нагружена внешним моментом на конце вала, то относительный угол закручивания будет:
6. При кручении вала возникает деформация сдвига между соседними сечениями, следовательно, при кручении поперечных сечений валов, возникают только касательные внутренние силы создающие крутящий момент.
Крутящие моменты в поперечных сечениях вала определяют методом сечений. При использовании уравнений равновесия:
Крутящий момент в поперечном сечении вала численно равен алгебраической сумме внешних моментов, которые приложены к оставленной для рассмотрения части вала.
Считаем крутящий момент положительным, если внешний момент по отношению к рассматриваемой части вала направлен по ходу часовой стрелки (рис.23).
Читайте также: Вибраторы глубинные с гибким валом для чего
Эпюра крутящих моментов представляет собой график изменения крутящего момента по длине вала. С помощью эпюры крутящих моментов определяют опасное сечение вала, то есть такое в котором действует наибольший крутящий момент.
2.4.2. Напряжение и деформация при кручении
В поперечных сечениях скрученного вала (рис.2.24) действует, только касательное напряжение , следовательно, крутящий момент представляет собой результирующий момент внутренних касательных сил, то есть действующий на бесконечно малых площадках поперечного сечения, его можно выразить:
где — расстояние или плечо элементарной силы относительно продольной оси вала;
Данная зависимость отражает статическую сторону работы сечения, но не позволяет определить значение касательных напряжений по известному крутящему моменту, так как в данном случае не установлен закон распределения касательных напряжений по сечению.
Рис. 2.24. Схема скрученного вала
Угол сдвига для некоторого поперечного сечения.
Тогда касательное напряжение прямо пропорционально расстоянию до оси вала.
Эпюра распределения вдоль радиуса сечения вала всегда имеет вид треугольника, если соблюдаются выше перечисленные условия (рис. 2.25). Если вал состоит из одного участка (то есть имеет постоянное сечение и постоянный по длине крутящий момент), то в данном волокне бруса будет постоянным по всей длине участка.
Рис. 2.25. Эпюра касательных напряжений
2.4.3. Расчет на жесткость и прочность при кручении
1. Прочность , (2.22)
— полярный момент сопротивления [ ] = [м 3 ]
— допускаемое касательное напряжение, устанавливается в зависимости от допускаемого напряжения при растяжении.
2. Условие жесткости бруса при кручении состоит в том, чтобы относительный угол закручивания φ0 не превосходил некоторого заданного допускаемого значения [φ0]
φ0 ≤ [φ] – условие жесткости; (2.23)
где φ0 – относительный угол закручивания;
[φ] – допускаемый относительный угол закручивания.
2.4.4. Пример расчета вала при кручении
Для стального трансмиссионного вала (рис. 2.26) G = 8·10 10 МПа:
1. Определите значение скручивающих моментов (подводимого к шкиву 0 и снимаемых со шкивов 1, 2, 3).
2. Постройте эпюры крутящих моментов.
3. Определите диаметры каждого участка ступенчатого вала из условия прочности. Окончательно принимаемые значения должны быть округлены до ближайших стандартных по ГОСТ 6636-69. Диаметр вала (мм): 30, 35, 40, 45, 50, 60, 70, 80, 90, 100, 110, 125, 140, 160, 180, 200.
4. Вычертите в масштабе эскиз ступенчатого вала.
5. Постройте эпюру углов закручивания относительно левого шкива на валу.
6. Проверьте жесткость вала при кручении и при недостаточной жесткости участков вала, определите их диаметры из условий жесткости.
Числовые данные варианта взять из приложения 11, схему варианта из приложения 12.
Схема нагружения и исходные данные.
| а | Р0 | Р1 | Р2 | Р3 | ω | [τ] | [φ] |
| м | кВт | рад/с | мПа | рад/м | |||
| 0,1 | 0,02 |
 |
Рис. 2.27. Расчетная схема и результаты расчетов
🔍 Видео
Сопромат. Построение эпюр вала при кручении. Я в вк https://vk.com/id4682924Скачать

11. Кручение ( практический курс по сопромату )Скачать

Кручение валаСкачать

Кручение. Часть 6 Жесткость валаСкачать

Кручение зажатого валаСкачать

Кручение. Расчет составного вала кольцевого сечения.Скачать

Сопротивление материалов. Лекция: кручение круглого стержняСкачать

Кручение. Построение эпюр крутящих моментов и углов закручивания.Скачать

Сопротивление материалов. Лекция: кручение тонкостенного профиляСкачать

Основы работы в среде Solidworks Simulation. Кручение цилиндрического валаСкачать

Как определить момент затягивания болта ГБЦ.Скачать

Основы сопромата. Задача 5. Расчет стержня на кручениеСкачать

Сопромат. Практическое занятие №1.4Скачать

Статически неопределимый вал. Расчет на прочность при крученииСкачать

Основы простого сопротивления. Часть 2. Кручение круглого валаСкачать

Как быстро рассчитать момент затяжки болтаСкачать

Динамометрический ключ как пользоваться, выставить момент затяжки, выполнять затяжку болтов!!!Скачать