Угол закручивания вала при жесткость

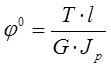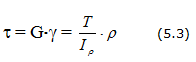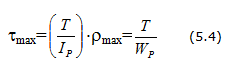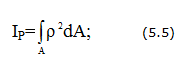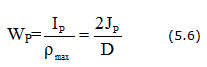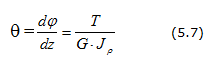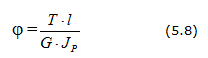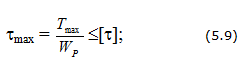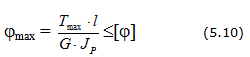
крутящего момента для отдельных участков (§ 16). Выберите материал расчетного вала и определите допустимое напряжение[t] для этого материала. Условия записи Секционная прочность 214 вала с максимальным значением крутящего момента(согласно диаграмме крутящего момента) (9.12).

Если вал достаточно длинный и отдельные секции достаточно сильно отличаются по величине крутящего Людмила Фирмаль

момента, то они должны быть ступенчато спроектированы. Диаметр вала каждой ступени рассчитывается по одной и той же формуле(9.12), но значения крутящего момента различны для разных участков в зависимости от графика крутящего момента. Учитывая, что можно написать формулу для расчета диаметра вала

из сплошного круглого вала Wp=уравнение (9.13: (9.16) Определить диаметр полой оси, заданный соотношением между размерами внутреннего и наружного диаметров из конструктивных соображений, т. е. коэффициент= — тогда, учитывая уравнение(9.11), из уравнения (9.13)следует:: (9.17)) После определения размеров вала из условий прочности проверьте жесткость вала по формуле (9.14).

• Допустимый относительный угол поворота вала составляет 0,3°для каждого метра статической нагрузки[0′] — длина вала, переменная нагрузка[0°1=0,25°, ударная нагрузка[0 ′ 4=0,15°]. Учитывая, что формула (9.14) представляет угол закрутки в радианах, значение данного допустимого угла преобразуется в радианы, и в испытании выполняется условие жесткости (9.14), в противном случае размеры вала должны выбираться из условия жесткости(9.15).): Подставляя в эту формулу формулу момента полярной инерции, находим ее для непрерывной оси (9.18) Для полого вала Иногда при расчете вала

известно, что передаваемая мощность n равна лошадиным силам, а число оборотов-n в минуту. В этом деле 21 крутящий момент формулы может быть выражен непосредственно в терминах мощности n и числа оборотов n, исходя из Формулы (3.1): МК=71 620-кгс*(9.20) мощность/(задается в киловаттах, когда крутящий момент определяется по формуле (3.2): МК-97 360-кгс * см.(9.21）) >

27, например. Найти мощность, передаваемую валом, диаметр Людмила Фирмаль

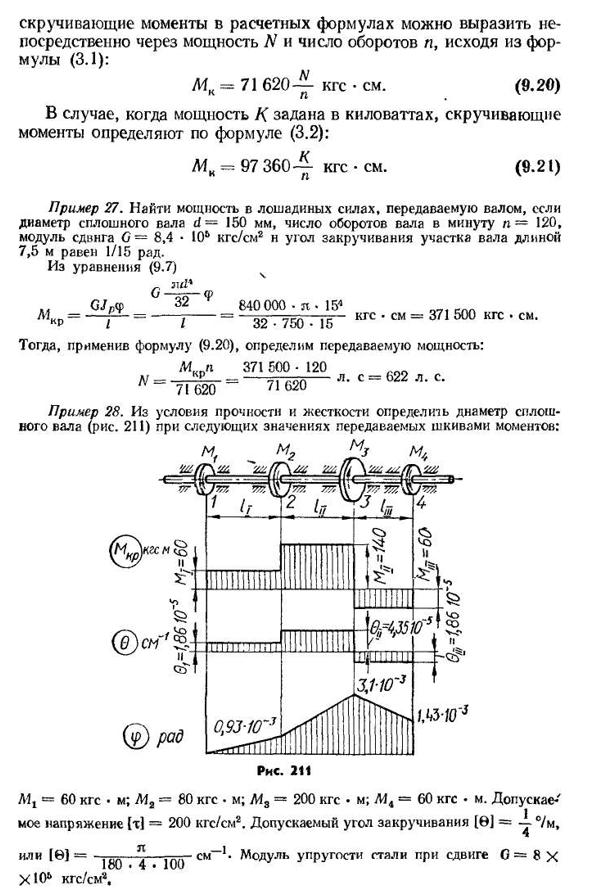
сплошного вала d-150мм, число оборотов вала n-120 в минуту, модуль сдвига G— 8,4 • 10 длина участка оси кгс / см2н с углом кручения 7,5 м составляет 1/15 Радиана. Из уравнения(9.7) И ой.. GJpat/7=/7 / =50 см h=J=90 см. В этом случае одна из секций фиксируется (рис. 211 настоящего раздела/). В пределах каждой секции 0-const угол кручения каждой секции изменяется по линейному закону,B, MD. Max=M V и формула на основе L\ymk В (А+Б) л[т] *

Видео:Расчет вала на прочность и жесткость. Эпюра крутящих моментовСкачать

Техническая механика

Сопротивление материалов

Видео:КРУЧЕНИЕ ВАЛА. Касательные напряжения. Сопромат.Скачать

Деформация кручения

Расчеты на прочность и жесткость при кручении

Условие прочности бруса при кручении заключается в том, что наибольшее касательное напряжение, возникающее в нем, не должно превышать предельно допустимое. При этом расчетная формула на прочность имеет вид:

где [τ_кр] — предельное допускаемое напряжение.

При практических расчетах, определяя предельные допускаемые напряжения для различных материалов, используют зависимость между напряжениями при растяжении и напряжениями при кручении, которая для стали и чугуна имеет вид:

(здесь [σ_р] — справочная или определяемая экспериментально величина, (предельное допустимое напряжение растяжения) характеризующая материал бруса (вала).

Кроме требования прочности к валам предъявляются требования жесткости, которое заключается в том, что угол закручивания участка вала длиной 1 м не должен превышать предельной величины, определяемой требованиями конструкции. Допускаемый угол закручивания 1 м длины вала задается в градусах и обозначается [φ₀°] .
Расчетная формула на жесткость при кручении имеет вид:

Читайте также: Лепестковый клапан для компрессора из чего сделать

В реальных механизмах обычно допускаются углы закручивания валов в пределах [φ₀°] = 0,25. 1 градус/м.

Пример решения задачи на кручение

Определить минимальный допустимый диаметр вала d , передающего крутящий момент М_кр = 464 Нм, если допускаемое напряжение кручения [τ_кр] = 30 МПа.

Решение

По известному передаваемому крутящему моменту можно определить момент сопротивления кручению:

W_r = М_кр / [τ_кр] = 464 / 30 х 10 6 = 15,6 х 10 -6 м 3 .

Из зависимости между моментом сопротивления кручению и диаметром вала W_r ≈ 0,2D 3 находим минимальный допустимый диаметр:

D ≈ 3 √( W_r / 0,02) ≈ 43 мм (здесь и далее √ — знак корня).

Округляя найденное значение диаметра до стандартной величины (в большую сторону), принимаем D = 45 мм.

Потенциальная энергия деформации при кручении

Представим себе круглый цилиндрический брус (вал) постоянного сечения, жестко защемленный одним концом и нагруженный на другом конце моментом, приложенным статически, т. е. медленно возрастающим от нуля до какого-либо значения Т .
Полагаем, что момент остается в пределах, когда нагрузка и деформация пропорциональны, т. е. справедлив закон Гука.

Момент Т вызывает в брусе деформацию кручения и при этом совершает работу W , которая аккумулируется в виде потенциальной энергии деформации U , причем пренебрегая незначительными потерями энергии (например, на нагрев бруса), можно считать, что W = U .

Работа в случае статического нагружения равна: W = Т φ / 2 , где φ — полный угол закручивания бруса.
Так как Т = М_кр , то справедливо равенство:

U = W = Т φ / 2 = М_кр 2 l / (2Gl_r) .

При одновременном действии нескольких моментов или ступенчатом изменении размеров поперечного сечения брус разбивают на однородные участки и потенциальную энергию деформации всего бруса определяют как сумму потенциальных энергий этих участков.

Материалы раздела «Деформация кручения»:

Видео:КРУЧЕНИЕ. ЭПЮРЫ ЗАКРУЧИВАНИЯ. Углы поворота. СопроматСкачать

5.5. Расчет валов на жесткость

5.5. РАСЧЕТ ВАЛОВ НА ЖЕСТКОСТЬ

За меру жесткости принимают относительный угол закручивания, то есть угол, приходящийся на единицу длины вала Условие жесткости: ≤ [θ] где [θ] имеет размерность рад/м. Чаще пользуются условием Допускаемое значение угла [θ°] закручивания зависит от назначения вала. Принимают [θ°] = (0,3–1,0) град/м. При расчете валов на прочность и жесткость часто задают мощность N, передаваемую валом и частоту его вращения n. Для вычисления крутящего момента по этим данным удобно воспользоваться таблицей Пример 5.1. Расчета вала на прочность и жесткость I. Определение внутренних усилий Значение ведущего момента Мвед определим из условия равновесия вала: Σ Мх = 0; Мвед – М1 – М2 – М3 = 0, откуда Мвед = М1 + М2 + М3 = 5 + 7 + 6 = 18 кН·м. Для расчетов на прочность и жесткость необходимо найти положение опасных сечений и величины крутящих моментов, действующих в этих сечениях вала (рис. 5.3, а). Воспользовавшись методом сечений определим внутренние усилия и построим эпюру крутящих моментов (рис. 5.3, б). Опасными являются все сечения на участке II, где действует Тmax = 12 кН·м. II. Проектный расчет валов сплошного и полого сечений Предварительно найдем допускаемое касательное напряжение, связанное с допускаемым нормальным напряжением. Принимаем по третьей теории прочности [τ] = 0,5 [σ] = 0,5·160 = 80 МПа. Из условия прочности и жесткости при кручении находим требуемые значения полярных момента сопротивления и момента инерции Из условия прочности и жесткости выполнить проектный расчет: определить диаметры валов в двух вариантах исполнения – сплошного и полого с коэффициентом пустотелости с = d/D = 0,8. Результаты округлить согласно ГОСТу. Построить эпюры углов закручивания вала. Валы сопоставить по металлоемкости и жесткости. Дано: М1 = 5 кН·м; a = 0,6 м; М2 = 7 кН·м; b = 0,8 м; М3 = 6 кН·м; с = 0,7 м; [σ] = 160 МПа; [θ] = 0,8 град/м. Рис. 5.3. Схема нагружения вала (а), эпюра крутящих моментов (б), эпюры углов закручивания сплошного (в) и полого (г) валов Результаты расчетов Форма сечения Сплошное Полое Момент сопротивления Углы закручивания характерных сечений вала сплошного и полого сечений Момент инерции принятый Жесткость сечения G·Ip = 80·109·1,19·10-5 = 0,955·106 Н·м2 G·Ip = 80·109·1,20·10-5 = 0,961·106 Н·м2. Углы закручивания участков вала Углы закручивания характерных сечений вала Строим эпюры углов закручивания сплошного и полого валов (рис. 5.3, в и г) III. Сопоставление металлоемкости валов двух вариантов Металлоемкость вала определяется его объемом, то есть произведением длины на площадь поперечного сечения. Поскольку длина вала неизменна, сопоставим площади поперечных сечений сплошного вала с полым Выводы: 1. Из условий прочности и жесткости найдены диаметры вала двух вариантов исполнения, сплошного и пустотелого: 105 и 120 мм соответственно. 2. Вычислены деформации валов на каждом из участков, построены эпюры углов закручивания валов сплошного и пустотелого. Жесткости валов практически одинаковы. 3. Сопоставлены металлоемкости валов двух вариантов исполнения. Расход металла для вала сплошного сечения вдвое больше, чем для вала пустотелого. Примечание. Полученный результат по сопоставлению металлоемкости валов ожидаем, поскольку достаточно большой объем материала, сосредоточенный около центра тяжести сечения, испытывает напряжения ниже допускаемого и вклад его в общую прочность конструкции невелик. Поэтому целесообразно убирать неработающий материал из этой области. Конструкции из полого сечения созданы природой: камыш, тростник, бамбук, злаковые культуры, трубчатые кости птиц и млекопитающих. В авиации и космонавтике используют полые валы, в строительстве – пустотные плиты перекрытий.

Читайте также: Валы для гибочного станка

Видео:Сопромат. Построение эпюр вала при кручении. Я в вк https://vk.com/id4682924Скачать

Расчеты валов на жесткость

Расчет вала на жесткость обязателентолько для особо важных машин, когда деформации вала существенно влияют на работу сопряженных с ним деталей, например зубчатых колес (относительный перекос колес может привести к поломке зубьев из-за усиления концентрации нагрузки), подшипников каче­ния (защемление тел качения в результате чрезмерного угла накло­на цапф вала) и др.

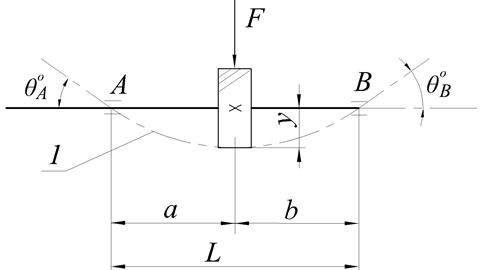
Различают изгибную и крутильную жесткость валов. Изгибную жесткость вала оценивают величиной угла наклона упругой линии вала (на рис. 1.5 обозначена цифрой 1) и максимальным прогибом вала “у” по зависимостям:

где θ 0 , у – фактические значения угла наклона упругой линии вала и его максимального прогиба;

[θ 0 ] – допус­тимый угол наклона упругой линии вала;

[у] – допус­тимый прогиб упругой линии вала.

Рис. 1.5. Схема к расчету вала на изгибную жесткость

Прогибы и углы наклона упругой линии валов определяют обыч­ными методами сопротивления материалов. Для простых расчетных случаев следует использовать готовые формулы, рассматривая вал как брус постоянного сечения приведенного диаметра [1, с. 332], а величина допустимого прогиба [у] в месте посадки на вал зубчатых колес может быть определена в зависимости от модуля колеса [2, с. 26]:

· для цилиндрических зубчатых колес [ y] = 0,01m;

· для конических и червячных колес [ y] = 0,005m.

Необходимая крутильная жесткость валов определяется различ­ными критериями. Для большинства валов крутильная жесткость не играет существенной роли, поэтому проверку крутильной жесткости валов выполняют только для трансмиссионных и торсионных валов. Угол закручивания цилиндрического участка вала длиной “l” при дейст­вии крутящего момента Твычисляют по зависимости [1, с.332]:

где j 0 – крутильная жесткость;

G – модуль сдвига; для стального вала G = 8 ×10 4 МПа;

J_p– полярный момент инерции поперечного сечения вала;

Читайте также: Производство вала технологический процесс

J_p = p × d 4 / 64 , мм 4 .

В ф. (1.14) отношение l / (G×J_p) = e – податливость рассчитывае­мого участка вала, тогда: j 0 = T× е.

Следует отметить, что приводы роботов и манипуляторов отно­сятся к высокоточным и поэтому упругие статические угловые дефор­мации кинематических цепей этих приводов могут сказываться на точности работы машины в целом. Другая особенность приводов робо­тов и манипуляторов: медленные и плавные перемещения в кинемати­ческих цепях этих приводов могут способствовать возникновению скачкообразных движений рабочих органов.

Так, например, при изме­нении направления вращения вала (реверс) сначала происходит осво­бождение вала от деформации кручения, а затем закручивание вала на тот же угол (если величина момента не изменилась), но в проти­воположном направлении. Возникающий при этом мертвый ход равен двойному углу закручивания:

Отсюда следует, что при недостаточной крутильной жесткости и значительной длине участка вала мертвый ход может оказаться недопустимо боль­шим и приведет к скачкообразному движению рабочего органа робота. Поэтому необходимо ограничение величины угла мертвого хода по ус­ловию j 0 _М.Х. ≤ [j 0 _М.Х.][6, с.311].

Видео:Сопромат №4: Расчет вала на прочность и жесткостьСкачать

iSopromat.ru

Для обеспечения прочности и жесткости вала при кручении, напряжения и деформации от крутящих моментов не должны превышать соответствующих допустимых значений.

Этот вид нагружения возникает при приложении к брусу пар сил, плоскости действия которых перпендикулярны его оси. Такие брусья принято называть валами.

Внешние пары, приложенные к валу, будем называть скручивающими моментами. Они могут быть сосредоточенными М₁, М₂, …, М_n или распределенными m по длине вала l .

Крутящий момент является равнодействующим моментом напряжений, возникающих в каком-либо сечении вала относительно его продольной оси.

Видео:Сопромат. Практическое занятие №1.4Скачать

Внутренний крутящий момент

При определении величины крутящего момента используется метод сечений. Суть его заключается в следующем: рассекаем вал сечением и отбрасываем одну из частей вала, расположенную либо справа, либо слева от сечения.

Обычно отбрасывают ту часть, к которой приложено больше скручивающих пар. Действие отброшенной части на рассматриваемую заменяют внутренним силовым фактором – крутящим моментом T . Затем из условий равновесия остановленной части вала определяют крутящий момент:

Таким образом, крутящий момент в каком либо сечении вала является уравновешивающей парой сил всех внешних скручивающих пар, приложенных либо слева, либо справа от рассматриваемого сечения.

Видео:11. Кручение ( практический курс по сопромату )Скачать

Напряжения при кручении

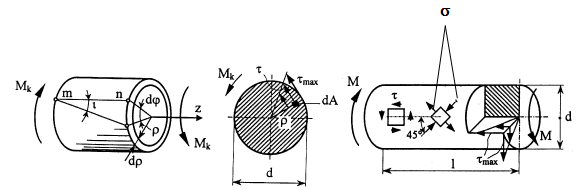
Распределение касательных напряжений

Максимальное касательное напряжение

Геометрические характеристики круглых сплошных сечений вала

Полярный момент сопротивления

Видео:Кручение. Часть 6 Жесткость валаСкачать

Деформации вала

Видео:Сопротивление материалов. Лекция: кручение круглого стержняСкачать

Условия прочности и жесткости вала

Расчет вала при кручении сводится к одновременному удовлетворению двух условий:

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Видео:Сопротивление материалов. Лекция: кручение тонкостенного профиляСкачать

Решение задач, контрольных и РГР

Стоимость мы сообщим в течение 5 минут
на указанный вами адрес электронной почты.

Если стоимость устроит вы сможете оформить заказ.

Видео:9.1 Расчет валов приводаСкачать

Набор студента для учёбы

— Рамки A4 для учебных работ
— Миллиметровки разного цвета
— Шрифты чертежные ГОСТ
— Листы в клетку и в линейку

• Свежие записи
  • Чем отличается двухтактный мотор от четырехтактного
  • Сколько масла заливать в редуктор мотоблока
  • Какие моторы бывают у стиральных машин
  • Какие валы отсутствуют в двухвальной кпп
  • Как снять стопорную шайбу с вала
  • Правообладателям
  • Политика конфиденциальности

  Механика © 2023
  Информация, опубликованная на сайте, носит исключительно ознакомительный характер

  
  

  источники:

  https://evakuatorinfo.ru/ugol-zakruchivaniya-vala-pri-zhestkost

  📽️ Видео

  Основы работы в среде Solidworks Simulation. Кручение цилиндрического валаСкачать

  

  Прочность и жесткость валов. Часть 9. Расчет на жесткость промежуточного вала (КЦ-редуктор)Скачать

  

  Почему он шумитСкачать

  

  Кручение валаСкачать

  

  Кручение. Расчет составного вала кольцевого сечения.Скачать

  

  Прочность и жесткость валов. Часть 6: Эпюры моментов выходного вала (цилиндрическая передача).Скачать

  

  Статически неопределимый вал. Расчет на прочность при крученииСкачать

  

  Основы простого сопротивления. Часть 2. Кручение круглого валаСкачать

  

  Кручение зажатого валаСкачать