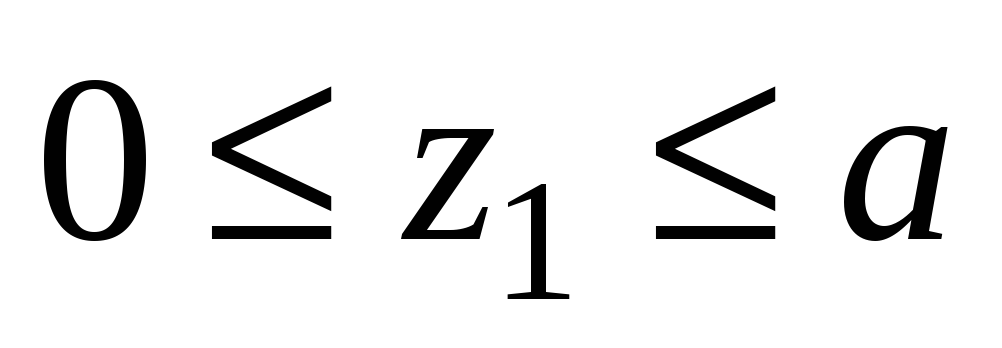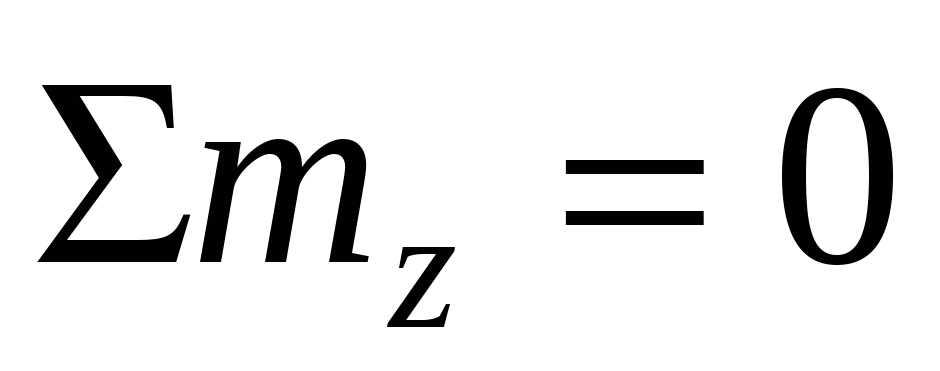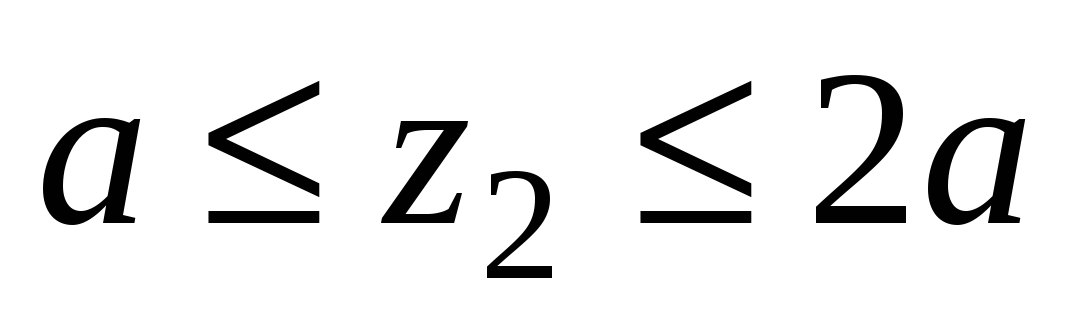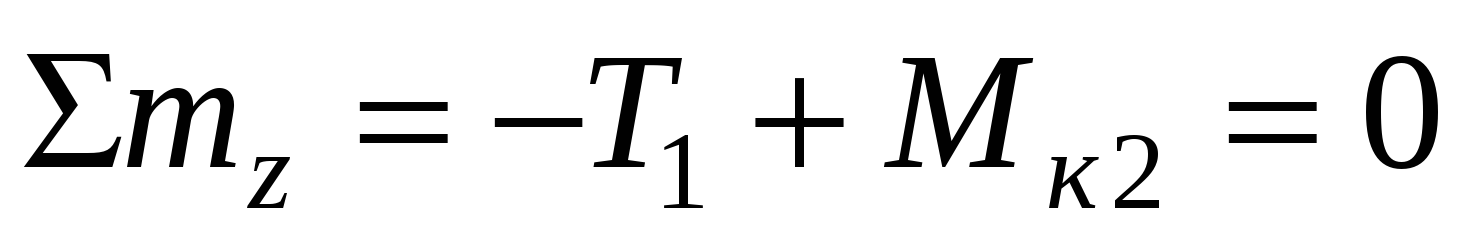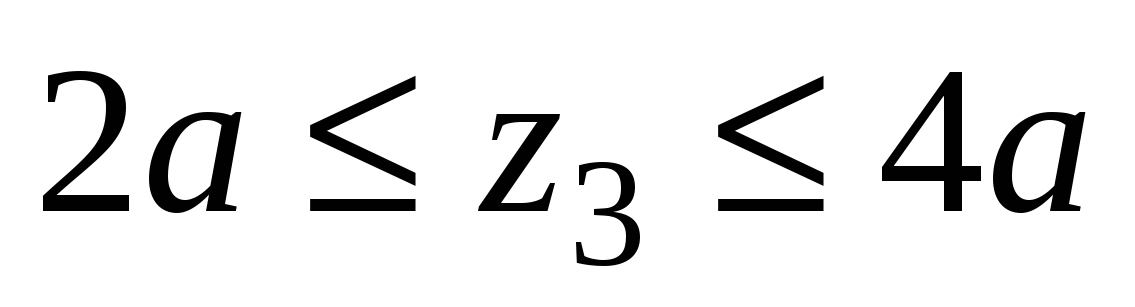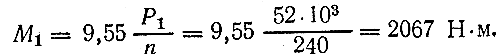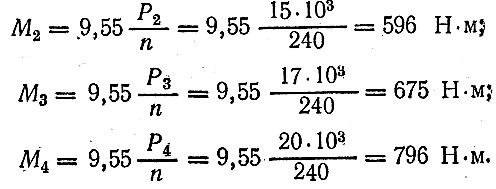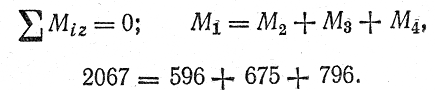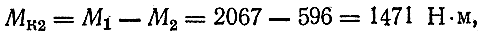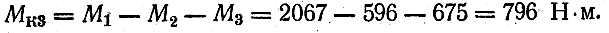Кручением называется такой вид деформации бруса, при котором в его поперечных сечениях возникает только один внутренний силовой фактор – крутящий момент T.
Брусья, испытывающие кручение, принято называть валами.
Видео:9.1 Расчет валов приводаСкачать

Внутренний крутящий момент
Внутренние скручивающие моменты появляются под действием внешних крутящих моментов mi, расположенных в плоскостях, перпендикулярных к продольной оси бруса.
Скручивающие моменты передаются на вал в местах посадки зубчатых колес, шкивов ременных передач и т.п.
Величина крутящего момента в любом сечении вала определяется методом сечений:
т.е. крутящий момент численно равен алгебраической сумме скручивающих моментов mi, расположенных по одну сторону от рассматриваемого сечения.
Правило знаков внутренних скручивающих моментов:
Положительными принимаются внутренние моменты, стремящиеся повернуть рассматриваемую часть вала против хода часовой стрелки, при рассмотрении со стороны отброшенной части вала.
В технике наиболее широко используются валы круглого поперечного сечения.
Теория кручения круглых валов основана на следующих гипотезах:
- поперечное сечение, плоское до деформации вала, остается плоским и после деформации;
- радиусы, проведенные мысленно в любом поперечном сечении, в процессе деформации вала не искривляются.
Видео:Деформация кручения Деформация изгибаСкачать

Напряжения при кручении
В поперечных сечениях вала при кручении имеют место только касательные напряжения.
Касательные напряжения, направленные перпендикулярно к радиусам, для произвольной точки, отстоящей на расстоянии ρ от центра, вычисляются по формуле:
где Iρ — полярный момент инерции.
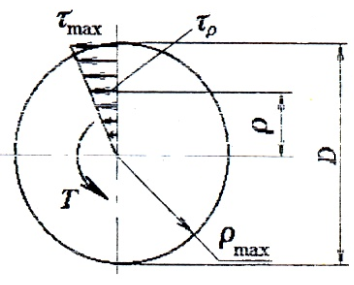
Эпюра касательных напряжений при кручении имеет следующий вид:
Касательные напряжения меняются по линейному закону и достигают максимального значения на контуре сечения при ρ= ρmax:
Здесь:
— полярный момент сопротивления.
Геометрические характеристики сечений:
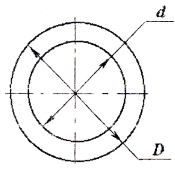
а) для полого вала:
б) для вала сплошного сечения (c=0)
в) для тонкостенной трубы (t 0,9)
где
— радиус срединной поверхности трубы.
Видео:Расчет вала на прочность и жесткость. Эпюра крутящих моментовСкачать

Деформации
Деформации валов при кручении заключаются в повороте одного сечения относительно другого.
Угол закручивания вала на длине Z определяется по формуле:
Если крутящий момент и величина GIρ, называемая жесткостью поперечного сечения при кручении, постоянны, для участка вала длиной l имеем:
Угол закручивания, приходящийся на единицу длины, называют относительным углом закручивания:
Расчет валов сводится к одновременному выполнению двух условий:
- условию прочности:
- условию жесткости:
Для стальных валов принимается:
- допускаемое касательное напряжение
- допускаемый относительный угол закручивания
Используя условия прочности и жесткости, как и при растяжении – сжатии можно решать три типа задач:
- проверочный расчет, заключающийся в проверке выполнения условий прочности и жесткости при известных значениях крутящего момента, размеров и материала вала.
- Проектировочный расчет, при котором вычисляются диаметры:
при этом берется большее из найденных значений, а затем принимается стандартное значение по ГОСТ. - Определение грузоподъемности вала:
- из условия прочности
- из условия жесткости
- из условия прочности
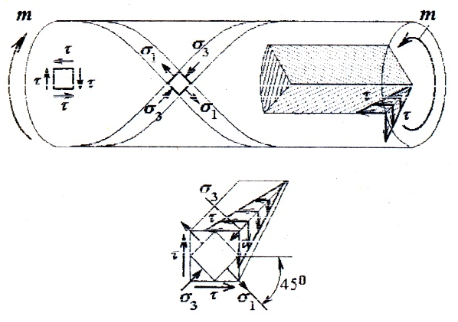
При кручении, наряду с касательными напряжениями в поперечных сечениях, в соответствии с законом парности, касательные напряжения возникают и в продольных сечениях. Таким образом, во всех точках вала имеет место чистый сдвиг.
Главные напряжения σ1 = τ, σ3 = -τ наклонены под углом α=±45 о к образующей.
Потенциальная энергия упругой деформации определяется по формуле
или для участка вала при постоянном T и GIρ
Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач
✔ Выполнение учебных работ
✔ Помощь на экзаменах
Видео:11. Кручение ( практический курс по сопромату )Скачать

Разработка открытого урока на тему «Сдвиг и кручение»
Методика – форма общения педагога с аудиторией. Каждый преподаватель постоянно ищет и испытывает новые способы раскрытия темы, возбуждению такого интереса к ней, который способствует развитию и углублению интереса к обучению. Предлагаемая форма проведения занятия позволяет повысить познавательную деятельность, так как обучающиеся на протяжении всего урока самостоятельно получают информацию и закрепляют ее в процессе решения задач. Это заставляет их активно работать на уроке. «Тихое» и «громкое» обсуждение при работе в команде дает положительные результаты при оценке знаний. Элементы «мозгового штурма» активизируют работу на занятии. Совместное решение задачи позволяет менее подготовленным студентам разобраться в изучаемом материале с помощью более «сильных» товарищей. То, что они не смогли понять со слов педагога, может быть объяснено им еще раз более подготовленными товарищами.
Некоторые проблемные вопросы, задаваемые преподавателем, приближают обучение на уроке к практическим ситуациям. Это позволяет развивать логическое, инженерное мышление. Оценка работы каждого студента на уроке также стимулирует его деятельность.
Все выше сказанное говорит о том, что данная форма урока позволяет получить глубокие и прочные знания по изучаемой теме, активно участвовать в поиске решения задач.
Содержимое разработки
План учебного занятия № 29
Дисциплина Техническая механика
2. Тип занятия комбинированное
вид занятия урок-соревнование
3. Цель Формирование специальных компетенций по теме «Сдвиг и кручение»
1. Сформулировать основные понятия деформации – сдвиг и кручение
2. Дать основы практического расчета внутренних силовых факторов при кручении
3. Рассмотреть применение кручения в производстве
1. Прививать студентам аккуратность и четкость при выполнении схем и эпюр, внимательность при выполнении расчетов,
2. Добиваться активности и высокой работоспособности студентов на уроке.
3. Способствовать формированию у учащихся исследовательских умений и навыков.
1 Развивать навыки реализации теоретических навыков в практической деятельности;
2 Развивать пространственное, логическое и инженерное мышление
3 Развитие интереса к будущей профессии через содержание учебного материала
5.1Учащиеся должны понимать сущность сдвига и кручения, основные этапы построении эпюр крутящих моментов
5.2 Учащиеся должны иметь ценностные установки : уважительного отношения и полезной работы в команде , самостоятельного анализа и пространственного мышления, контроля и самоконтроля
5.3Учащиеся должны уметь: делать выводы и заключения, максимально использовать самостоятельность при решении задач, строить эпюры, расчленять задачу на логические законченные части
6Межпредметные связи: математика, черчение, материаловедение, техническое обслуживание и ремонт оборудования
7. Комплексное учебно-методическое обеспечение : макет для демонстрации деформации «Кручение», УМК, учебники, ПО Power Point , ActivStudio
Управленческая деятельность преподавателя
Деятельность учащихся на каждом этапе
Средства каждого этапа занятия
Выдаёт студентам опорный конспект и лист оценок
Сообщает тему и цель урока.
Настраивает учащихся на занятие
Раздаёт карточки самооценивания
Настрой на позитивную работу.
Воспринимают информацию, сообщаемую преподавателем
В течении всего занятия на доске ведётся счёт баллов для каждой команды
2 Повторение пройденного материала
Группа разделена на 2 команды.
1 Игра сопромат с динозавриками
2 Определить деформцию(соедини стрелками)
3 По видео определить виддеформации
Самопроверка по ответам на вопросы технического диктанта
Единица измерения напряжения (ответ: Паскаль).
Внутренний силовой фактор, деленный на геометрическую характеристику сечения (ответ: напряжение).
Способность материала восстанавливать свою форму и размеры после снятия нагрузки (ответ: упругость).
Способность материала давать большие остаточные деформации (ответ: пластичность).
Изменение формы и размеров тел под действием нагрузки (ответ: деформация).
Ученый, именем которого назван модуль упругости (ответ: Юнг).
. Деформация, при которой внутренним силовым фактором является поперечная сила (ответ: сдвиг)
Деформация, внутренним силовым фактором которой является
продольная сила (ответ: растяжение).
Участвуют в игре, получают балл для команды
Отвечают на вопросы технического диктанта
Участвуют во взаимооценке
Меняются карточками, проводят проверку по готовым ответам(1 команда проверяет оветы 2, и наоборт)
Работа с интерактивной доской
(эпиграф – видео О сколько нам открытий чудных… )
Ведёт объяснение нового материала с элементами беседы, решением проблемных ситуаций и видеофильмами по плану Предварительно дано задание – определить связь изучаемой темы с будущей профессией и производством.
1 Чистый сдвиг. Закон Гука для сдвига.
Видео – история закона Гука
2 Доклад «Роберт Гук» (студент)
3. Испытания материалов при кручении
(По видео определить вид эксперимента на кручение)
5 Эпюры крутящих моментов.
Работают с опорным конспектом, решают проблемные ситуации, участвуют во взаимном обмене мнениями
Отвечают на вопросы после просмотра видеороликов.
Формулируют основные понятия
4 Проверка понимания учащимися изученного материала
Продолжаем соревнование. Вопросы командам
1 Вращающий момент на ведущем шкиве М1=5000Нм Определите направление и значение М2 на ведомом шкиве. Постройте эпюру крутящих моментов
2 Укажите, какие участки вала испытывают деформацию кручения?
3 Укажите, какая точка соответствует сечению, где установлен ведущий шкив?
4 Какое расположение шкива более рационально?
5 Определите крутящий момент, Ма, если Мв = 800, Мс = 700Нм, М d = 1100Нм
Постройте эпюры крутящих моментов на участках
Решают проблемные ситуации
В соревновании ведётся счёт индивидуально — смайлики
1 Анализирует результаты выполнения учащимися заданий, оценивает работу учащихся
Оценивает результаты работы студентов на уроке:индивидуалтная оценка+ оценка команды+оценка преподавателя = итоговая
2 Сообщает, что необходимо подготовить к следующему занятию
Записывают домашнее задание в конспект
Рефлексия по методу 5 пальцев
Лекция 2.8 Сдвиг и кручение
1 Чистый сдвиг. Закон Гука для сдвига
3 Испытания материалов при кручении
5 Эпюры крутящих моментов.
При проектировании сооружений и машин приходится выбирать материал и поперечные размеры для каждого элемента конструкции так, чтобы он надежно, без риска разрушиться или исказить свою форму, сопротивлялся действию внешних сил, передаваемых другими деталями механизма, т. е. чтобы была обеспечена нормальная работа этого элемента. Требование прочности конструкции иногда связано с увеличением размеров поперечного сечения детали. Требование экономичности, наоборот, вызывает необходимость их уменьшения, так как увеличение размеров ведет не только к увеличению прочности, но и к утяжелению конструкции, перерасходу материала, к повышению стоимости механизма.
Основная задача — разработка методов, позволяющих подбирать надежные и наиболее экономичные размеры поперечных сечений элементов конструкций, а также, наиболее целесообразную их форму. Кроме того, в сопротивлении материалов часто приходится решать и обратную задачу, т. е. проверять элементы конструкции на прочность, жесткость, устойчивость, а также находить допускаемые нагрузки, при которых конструкция может надежно работать.
Задачей лекции является определение внутренних силовых факторов и построение эпюры крутящих моментов
1 Чистый сдвиг. Закон Гука для сдвига.
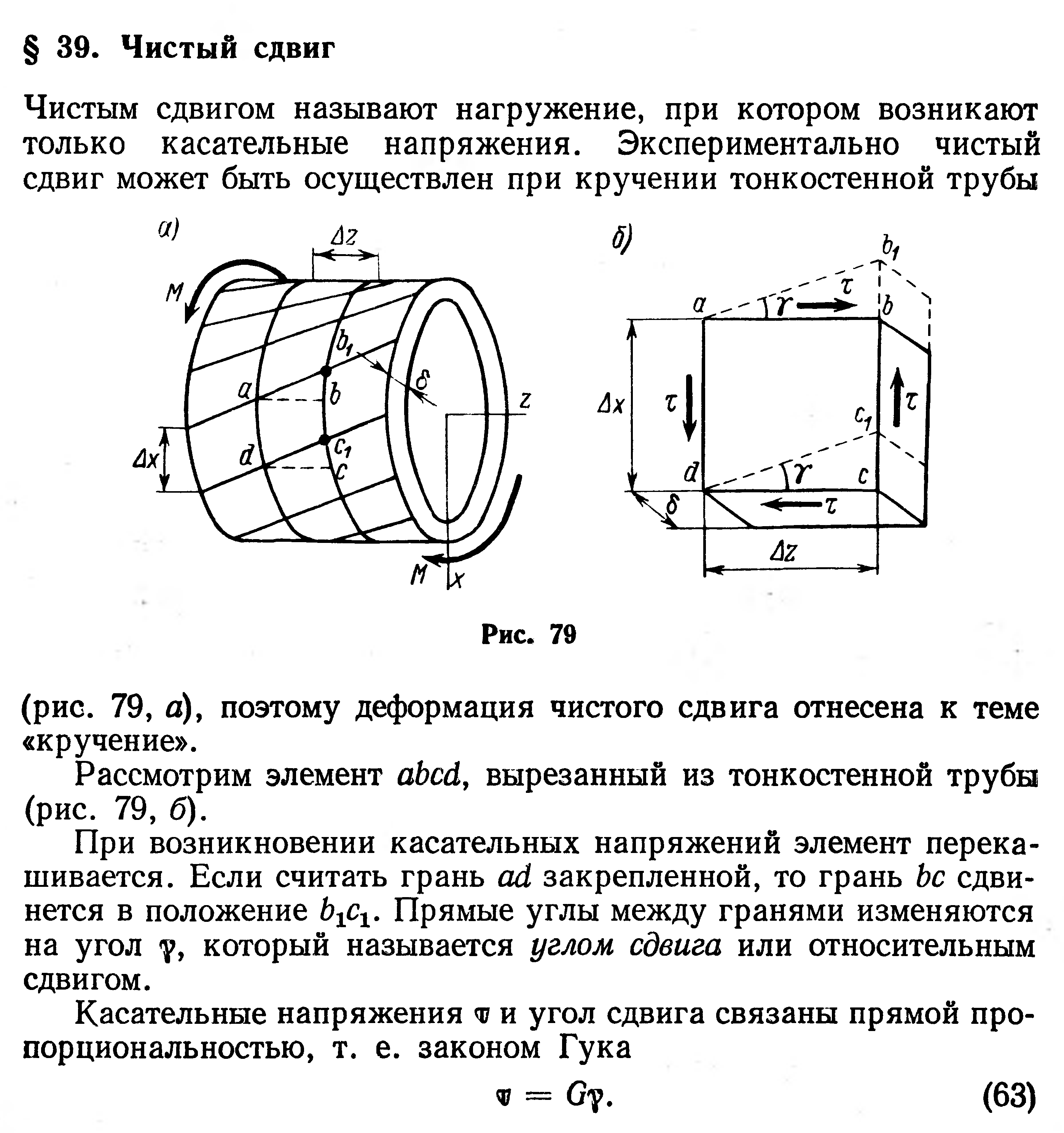
Экспериментально чистый сдвиг может быть осуществлен при кручении тонкостенной трубы , поэтому деформация чистого сдвига отнесена к теме «кручение».
Рассмотрим элемент ab сd, вырезанный из тонкостенной трубы При возникновении касательных напряжений элемент перекашивается. Если считать грань ad закрепленной, то грань bссдвинется в положение b1c1. Прямые углы между гранями изменяются на величину γ. Угол γ ,представляющий собой изменение первоначально прямого угла между гранями элементарного параллелепипеда, называется углом сдвига. Касательные напряжения τ и угол сдвига γ, называемый также относительным сдвигом, связаны прямой пропорциональностью, то есть законом Гука:
Как первоначально был сформулирован закон Гука? – смотрим видеофрагмент
Каков закон Гука для растяжения и сжатия? – отвечают закон Гука — нормальные напряжения в поперечном сечении прямо пропорциональны относительной линейной деформации e
Входящая в эту формулу величина G называется модулем сдвига. Эта величина характеризует жесткость материала при деформации сдвига. Так как γ выражается отвлеченным числом, то модуль сдвига G, как и модуль продольной упругости Е, имеет ту же единицу измерения, что и напряжение: МПа, Н/мм2, кгс/см2.
Между модулем упругости Е и модулем сдвига G существует зависимость, которую приводим без вывода:
где μ — коэффициент поперечной деформации (коэффициент Пуассона).
Для стали μ = 0,25; G = 0,4, Е = 0,4·2·10 5 = 8.10 4 МПа. Приведенные соотношения между G и Е подтверждаются опытами.+
В 1678 г. вышла из печати его работа О восстановительной способности или об упругости. В ней содержатся результаты проведенных Гуком опытов с упругими телами. Это был первый печатный труд, в котором рассматривались упругие свойства материалов.. Гук описывает также опыты с винтовыми и спиральными пружинами, в частности часовыми, а такж& с “бруском сухой древесины, который изгибается и возвращается в первоначальное состояние, если одним концом его укрепить в горизонтальном положении, к другому же концу подвешивать нагрузки, прогибающие его вниз”. Он не только исследует прогибы такой консоли, но рассматривает и деформации продольных ее волокон и приходит к весьма важному заключению, что на выпуклой поверхности волокна при изгибе растягиваются, на вогнутой—сжимаются. Из всех этих экспериментов Гук извлекает важное заключение.“Совершенно очевидно, что правило или закон природы для всякого упругого тела состоит в том, что его сила или способность восстанавливать свое естественное состояние всегда пропорциональны той мере, на которую оно выведено из этого своего естественного состояния, совершено ли это путем его разрежения, отделения его частей одна от другой или же путем сгущения или уплотнения этих частей”.
Мы видим, что Роберт Гук не только установил соотношение между величиной сил и производимыми ими деформациями, но и указал ряд экспериментов, где этим соотношением можно воспользоваться для решения некоторых весьма важных вопросов. Это линейное соотношение между силой и деформацией, известное как закон Гука, и послужило фундаментом, на котором впоследствии получила свое дальнейшее развитие механика упругих тел.
3 Испытания материалов при кручении
Многие детали машин подвергаются действию скручивающих нагрузок. Проводя испытания на кручение этих деталей, производители могут симулировать реальные условия эксплуатации, проверять качество продукции, утверждать дизайн и подбирать подходящие технологии производства.
Типы испытаний на кручение
Испытания на кручение можно проводить, применяя только вращательные или применяя осевые (растягивающие или сжимающие) и скручивающие нагрузки. Типы испытаний на кручение варьируются в зависимости от продукции, однако, их можно классифицировать, как испытания на разрушение, контрольные испытания и испытания на эксплуатацию изделия.
Только на кручение: к образцу прилагаются только скручивающие нагрузки.
При осевом и скручивающем нагружении: приложение осевых (растягивающих или сжимающих) и скручивающих нагрузок на образец испытания.
Испытание на разрушение: скручивание продукта, компонента или образца до разрушения. Разрушение можно классифицировать как физическое разрушение образца или изгиб/дефект образца.
Контрольное испытание: приложение скручивающей нагрузки и удержание данной нагрузки в течение заданного промежутка времени.
Эксплуатационное испытание: испытание готовых изделий или продукции, например, колпачков бутылок, переключателей, шприц-ручек или рулевых колонок для того, чтобы убедиться, что они сохраняют свои свойства при воздействии скручивающих нагрузок.
Рис. 5.2. Характер разрушения образцов из различных материалов при кручении:
а – чугун; б – сталь; в – дерево
По характеру разрушения при кручении можно судить, каким напряжениям (нормальным или касательным) хуже сопротивляется материал, из которого изготовлен вал.
Так, вал из хрупкого материала, хуже сопротивляющегося растяжению, чем сжатию, например, из чугуна, разрушается обычно по винтовой линии от действия главных растягивающих напряжений (рис. 5.2,а).
Вал, изготовленный из пластичной стали, разрушается по поперечному сечению б), т.к. нормальные напряжения для него оказываются менее опасными, чем касательные.
После просмотра видеоролика вы должны будете ответить на вопрос, какой тип испытания был проведён для образцов из стали и чугуна?
Какие разрушения происходят для образцов?
Как вы сформулируете определение для деформации кручение. Кручение — это такой вид деформации при котором…..
Кручением называется вид нагружения, при котором к брусу прикладываются внешние скручивающие моменты, а в поперечных сечениях возникает единственный внутренний силовой фактор — крутящий момент Mк (рис.5.1).
И правило знаков для эпюры крутящих моментов
Скручивающий момент, вращающий рассматриваемую часть стержня против хода часовой стрелки при взгляде на поперечное сечение, вызывает в этом сечении положительный крутящий момент, направленный по ходу часовой стрелки, противодействуя скручивающему моменту.
5 Эпюры крутящих моментов
Брусья, передающие крутящий момент называются валами. Внешние скручивающие моменты, как правило, передаются на вал в местах посадки на него шкивов, зубчатых колес и т.п. В большинстве случаев бывают заданы мощность, передаваемая валом, и числом оборотов, а величины скручивающих моментов определяются исходя из этих данных.
Пусть вал вращается с постоянной скоростью n об/мин. и передает мощность N Нм/с. Угловая скорость вращения вала равна 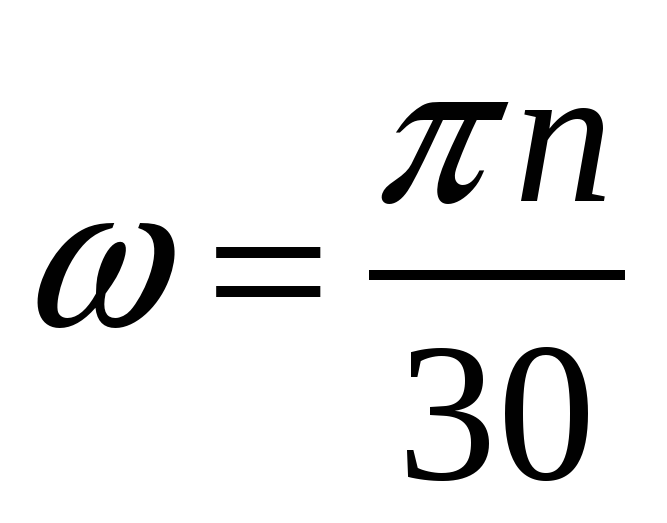
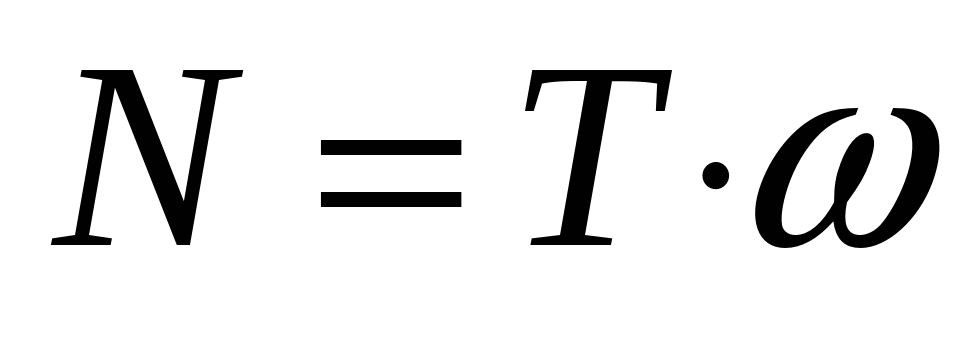
Скручивающий момент равен .
Видео:Валы карданные: верный способ измерения и основные комплектующиеСкачать

П остроение эпюр крутящих моментов
остроение эпюр крутящих моментов
Зная величины внешних скручивающих моментов и используя метод сечений, мы можем определить крутящие моменты, возникающие в поперечных сечениях вала.
Крутящий момент Мк в сечении вала числено равен алгебраической сумме внешних скручивающих моментов, действующих по одну сторону от сечения, при этом могут рассматриваться как левая, так и правая отсеченные части вала.
Воспользуемся методом сечений.
Рассечем участки вала (рис.5.2). Границами участков являются точки приложения скручивающих моментов.
Отбросим правую отсеченную часть.
Из уравнения равновесия отсеченной части найдем величину крутящего момента Мк, возникающего в сечении.
I участок
,
II участок
,
III участок
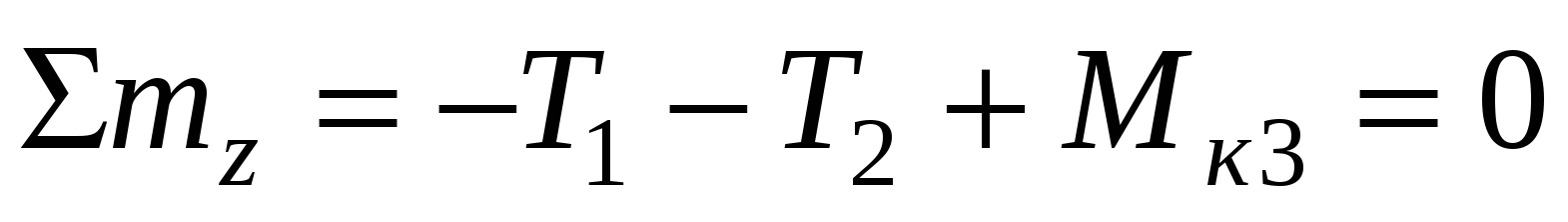
Для наглядного представления о величине крутящих моментов и характере их распределения по длине вала построим эпюры этих моментов. Построение эпюр крутящих моментов аналогично построению эпюр про
дольных сил при осевом растяжении-сжатии (рис.5.3).
Заметим, что в местах приложения внешних моментов ординаты эпюры скачкообразно изменяются на величину приложенного внешнего момента.
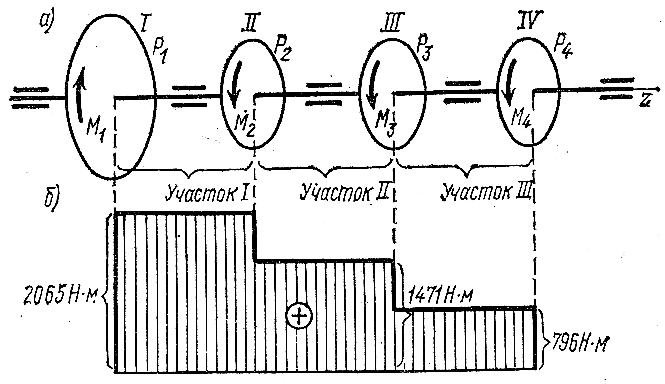
Пример 1. Построить эпюру крутящих моментов для вала по рис. а, если шкив 1 получает от двигателя мощность Р1 = 52 кВт при частоте вращения вала n = 240 об/мин, а шкивы II, III и I V соответственно снимают мощности Р2 = 15 кВт, Р3 = 17 кВт, Р4 = 20 кВт.
Рисунок 2.5.3
Решение . B ычисляем значения моментов, передаваемых шкивами.
Следует учесть, что согласно условию равновесия, пренебрегая трением в подшипниках, имеем:
Разобьем вал на три участка и приступим к построению эпюры крутящих моментов. Проведем поперечное сечение на первом участке между шкивами I и II и рассмотрим действие правой отброшенной части на левую. Слева в проведенном сечении возникает крутящий момент 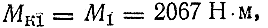
и на третьем участке между шкивами III и IV ;
На рис. 6 по вычисленным значениям М построена эпюра крутящих моментов.
💥 Видео
Детали машин. Лекция 4.1. Валы и оси.Скачать

9.4. Расчет валов и осейСкачать

Карданная передача, основы. Карданные шарниры не равных и равных угловых скоростей (ШРУСы)Скачать

Правило знаков при крученииСкачать

Подготовка вала к шлифовкеСкачать

Изгиб с кручениемСкачать

Кручение валаСкачать

Естествознание 5 Деформация Различные виды деформации Сила упругостСкачать

Кручение. Часть 1 Общие сведенияСкачать

Деформация Хаглунда – как появляется и что делать?Скачать

9.3. Конструктивные элементы валов и осейСкачать

Кручение. Часть 6 Жесткость валаСкачать

Прочность и жесткость валов. Часть 6: Эпюры моментов выходного вала (цилиндрическая передача).Скачать

Назначения валов и осей - учебный фильм СССРСкачать

Расчет вала на изгиб с кручениемСкачать



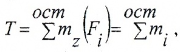
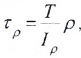
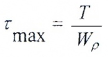
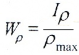
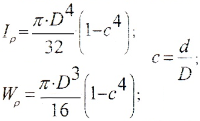
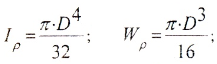
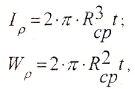
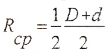
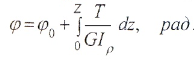
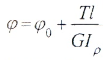
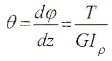
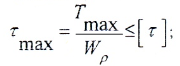
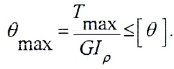
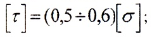
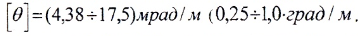
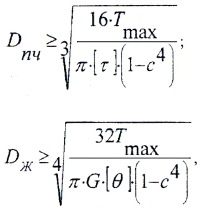
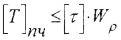
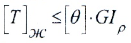
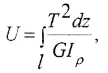
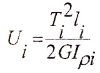
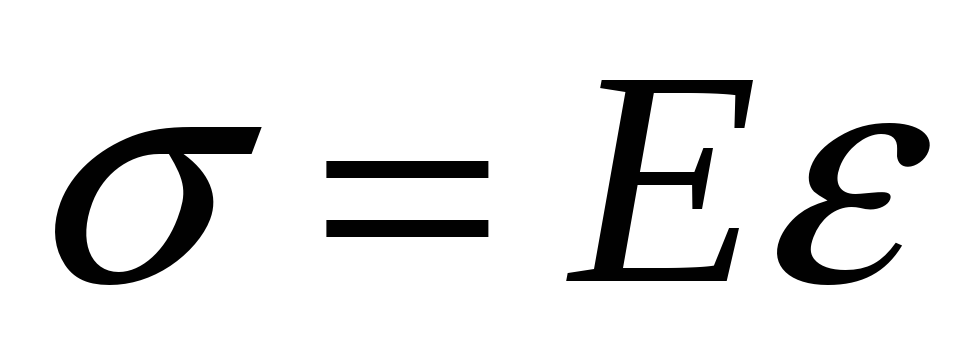


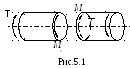
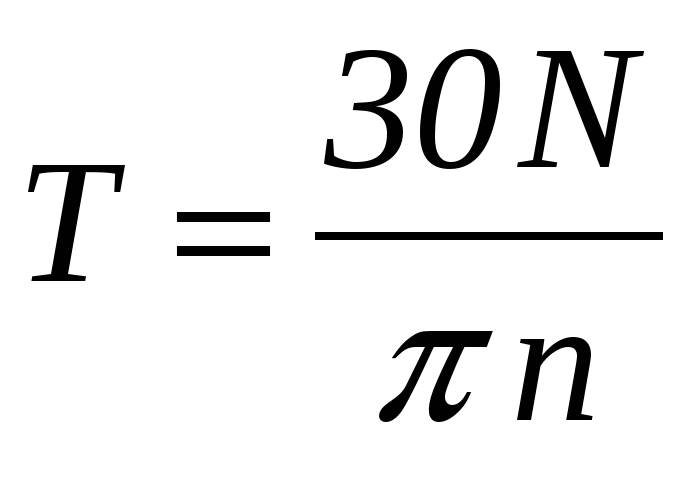
 остроение эпюр крутящих моментов
остроение эпюр крутящих моментов