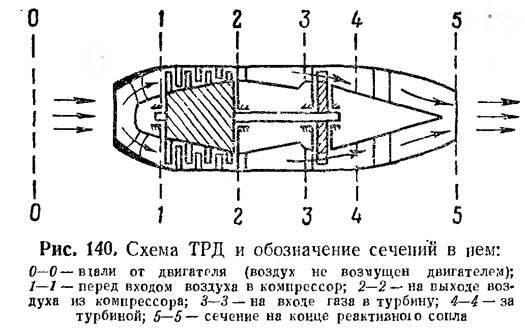
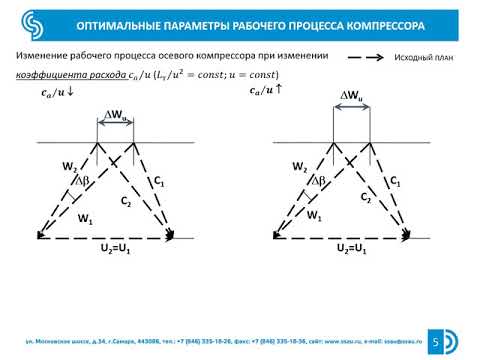
Это и есть УРАВНЕНИЕ НЕРАЗРЫВНОСТИ . Оно показывает, что секундный расход газа ч-з сечение 1—1 равен секундному расходу газа ч-з сечение 2—2. Это и есть основное свойс-тво установившегося дв-ия.
Для произвольного сечения Ғ с параметрами с и ρ
Формула дает значение сек-го массового расхода газа ч-з любое сечение струйки при усл-ии , что с , ρгаза остаются постоянными.
Но если газ течет по какому либо каналу (р-1.2), то его параметры не будут постоянными по сечению. Из-за трения ск-сть на поверхности канала равно нулю, а в центре она мак-симальна. В таком случае необх-мо суммир-ть расход для отдельных струек по сечению канала.
Где С и ρ — текущие ск-сти и плот-сти газа в сечении Ғ, а dҒί , — элемент площади.
На практике опыт показывает необходимо вводить понятие средние значение по ск-сти и плотности по сечению. Тогда формула будет,
G = Ғср с ср ρ ср.
ТЕМА 5 Уравнение сохранения энергии(Кн1 стр15).
Рассмотрим движ-е массы газа в каком-либо элементе ГТД (рис), и предположим, что на пути от сеч-я 1—1 до сеч-я 2—2 в общем случае газу сообщ-ся внешняя работа и внешнее тепло.
Согласно закону сохр-ия эн-ии при прохожд-и газа ч-з рассматриваемой элемент затра-ченая работа и теплота идут на повышение энтальпии (теплосодерж) и кинетической энергии газа, т.е.
Где ί1 (ί2) и с 2 1(с2) –энтальпия 1кг массы газа и ск-сть в сеч-и 1—1, (2 — 2); L и Qвн — внешняя работа и внешнее тепло, подведенные к 1кг массы газа.
Перепишем формулу в след-щем виде
Последнее уравнение можно трактовать так; полная энергия газа на входе в элемент (ί1+ с1 2 /2 ) плюс извне подведенные работа и теплота (L + Q) равны полной энергии на выходе из элемента.
Иначе говоря, Уравнение сохранения энергии предст-ет собой баланс энергии.
Необх-о отметить, что внешний вид уравнение сохранения энергии не зав-ит от того, учитыв-ся раб сил трения или нет. Это объясняется тем, что раб трения Lr, кот-я возникает из-за вязкости газа(р1,2), практ-ки полностью переходит в тепло Qr , поэтому в общем балансе -L+Q = 0. Таким образом, уравнение сохранения энергии незав-мо от внутренного процесса участвует только внешняя эн-ия, поэтому полная эн-ия
(ί2+ с2 2 /2 ) в конце процесса сохраняется. Тем не менее может существенно влиять на эффек-сть процесса.
Работа сил трения переходит в тепло и тем самым ув-ет энтальпию газа в конце процесса в элементе. В рез-тате, хотя сумма полной энергии (ί2+ с2 2 /2 ) не меняется, происходит перераспределение между энтальпией и кинет-кой эн-ией. Так как энтальпия ί2 растет , то величина с2 2 /2 должна уменьшится.
Очевидно, что чем больше увел-ние энтальпии газа за счет трения, тем больше степень необратимости процесса и меньше эффективность элемента.
ТЕМА 6 Уравнение сохранения энергии для входного устройства АД(Кн1 стр16).
Уравнение сохранения энергии (р 1.5) для вх-го устр-тва (сеч Н—Н и 1—1). Сеч-е Н—Н поместим в невозмущенном потоке, 1—1 – п-д компр-ром.
Между рассматриваемыми сечениями внешняя раб не подводится и не отводится, поэто-му L=0. Что же касается внешнего тепла, например, в случае впрыска жидкости в в-хо-заборник, то происх-т отвод тепла, т.к жидкость испаряется и отнимает тепло от в-ха (Жидк впрыск-ся в в-хозаборник для форсажа дв-ля в жаркую погоду).
Кроме того, на разл-ных режимах раб-ы дв-ля может происх-ть незнач-ный обмен тепла
ч-з стенки в-ха заборника, но этим обычно пренебрегают.
где V— ск-сть набег-щего потока (ск-сть полета). При отсутствии впрыска жидкости
Уравнения показывает, что при отсутствии эн-гообмена с внешней средой полная эн-ия в-ха вдоль оси вх-го устр-тва ост-ся пост-ной. Но т.к в в-хозабор-ке поток тормозится
(с1 ίн ). Если ввести в рассмотрение параметры заторможенного потока, принимая ί+ с 2 /2 = ί*, то уравнение примет вид
ί*н= ί*1. Но т.к ί = ср Т1 и ί * = ср Т * , где ср – теплоемкость в-ха, получим
Видео:Курс ""Турбомашины". Раздел 3.1.1. Принцип действия ступени компрессораСкачать
Т.е при отсутствии теплообмена энтальпия и темп-ра заторможенного потока в в-хозабор-нике сохр –ся пост-ными.
Для сжатия в-ха к компр-ру подв-ся внеш-яя раб L, поэтому L = Lк. Кроме того, здесь так же возможен отвод тепла. Во-первых, потому что при впрыске жидкости может не успеть испариться в в-хезаборнике, тогда испарение продолжается и в компр-ре, во-вторых, т.к. при сж-ии в-х нагр-ся, часть тепла может отводиться ч-з корпус компр-ра в окружающую среду (последним из-за малости пренебрегают).
Читайте также: Компрессор воздушный асо 500
В случае, когда отвод тепла отсут-ет и Qвн = 0
Уравнение показ-ет, что при отсутствии теплообмена с внешней средой затраченная на валу компр-ра работа идет на повыш- ие энтальпии заторможенного потока.
где ср—ср-яя теплоемкость в-ха, ср= R R/ R-1, Lк = R R/ R-1 × (Т * 2 – Т * 1).
Для в-ха при умер-ных темпер-х: R = 1,4; R = 287,3 Дж/(кг ·К); m = 0,0404 кг ·К/Дж 0,5 ;
Для газа R = 1,33; R = 287,5 Дж/(кг ·К); m = 0,0395 кг ·К/Дж 0,5 ;
ТЕМА 7 Уравнение сохранения энергии для камеры сгораня(Кн1 стр18).
Уравнение сохранения энергии для К.С. (сеч 2—2 и 3—3, рис 1.6).
В К.С. внешняя раб не подвобится и неотводится от нее, поэтому L = 0, ί*2 + Qвн = ί*3 или Q = ί*3 – ί*2 = ср (Т * 3 – Т * 2),
Т.е. подведенное внешнее тепло идет на повыш-ние энтальпии заторможенного потока.
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Уравнения энергии компрессорных процессов
Компрессоры
Степень повышения давления ε – отношение давления воздуха на выходе из машины к дав-лению на ее входе (ε = р2 / р1).
Компрессоры сжимают воздух при ε >> 1,15 и имеют искусственное (водяное или воздушное) охлаждение.
По уровню развиваемого давления:
а— вакуум-компрессоры – это машины, которые отсасывают газ из пространства с давлением ниже атмосферного;
б— компрессоры низкого давления – предназначены для нагнетания газа при конечном давле-нии 0,15…1,2 МПа (1,5…12 кгс/см 2 );
в— компрессоры среднего давления 1,2…10 МПа (12…100 кг/см 2 );
г— компрессоры высокого давления 10…100 МПа (100…1000 кг/см 2 );
д— компрессоры сверхвысокого давления с конечным давлением более 100 МПа (1000 кг/см 2 ).
Основные параметры компрессоров:
– объемная подача Q (исчисляется при условиях всасывания),
– начальное р1 и конечное р2 давления и степень повышения давления ε,
– частота вращения n и мощность машины N.
Компрессоры по принципу действия разделяются на объемные и лопастные.
Видео:Курс ""Турбомашины". Раздел 2.4 Уравнение энергии в мех. форме в отн.движении (лектор Батурин О.В.)Скачать
Объемные машины – поршневые и роторные.
Лопастные машины – центробежные и осевые.
Компрессоры также различаются по виду охлаждения – с водяным или воздушным охлажде-нием.
Поршневые компрессоры могут развивать давление до 250 МПа (2500 кг/см 2 ) и обладают производительностью до 2000 м 3 /мин.
Центробежные компрессоры – до 100 МПа (1000 кг/см 2 ) при той же производительности.
Теория компрессорного процесса
В теории компрессорных машин, работающихпри конечном давлении до 10 МПа (
100 кгс/см 2 ), используют уравнение состояния идеального газа (уравнение Менделеева-Клайпе-рона):
р – давление воздуха (Па) при абсолютной температуре в градусах Кельвина Т (ºК), ρ (кг/м 3 ) – плотность газа при той же температуре.
R – универсальная газовая постоянная, различная для разных газов, но не зависящая от темпе-ратуры и давления. Для воздуха R = 287 Дж/(кг∙ºК).
При сжатии воздуха до 10 МПа при температурах более 273 ºК применение уравнения (1) в расчетах компрессорных машин дает погрешность не более 2%.
Основные уравнения процессов сжатия и расширения, происходящих в компрессорах:
— политропный процесс: р/ρ n = Const; рv n = Const; (4)
— адиабатный процесс: р/ρ k = Const; рv k = Const; (5)
— изотермический процесс: р/ρ = Const; рv = Const; (6)
Политропный процесс – это термодинамический процесс, во время которого удельная теп-лоёмкость газа остаётся неизменной: с = δQ/δТ = Const, т. е. отношение приращения теплоты воздуха к приращению его абсолютной температуры не изменяется. Он является наиболее общим видом термодинамического процесса и протекает в поршневых компрессорах при n = 1,4.
Частными случаями политропного процесса являются:
-изотермический процесс, когда δТ = 0 (температура не изменяется),
-и адиабатный процесс, когда δQ = 0 (количество теплоты не изменяется).
Адиабатным называют процесс без теплообмена с внешней средой. Такой процесс имеет местов центробежных и осевых компрессорах.
Графики, отображающие указанные процессы, называются соответственно: политропа и ади-абата.
n – политропный показатель, определяемый через отношение: n = (с – ср) / (с – сV),
где с – теплоёмкость газа в данном процессе, ср и сV – теплоемкости воздуха газа при посто-янном давлении и постоянном объеме соответственно.
Читайте также: Холодильники с 2мя компрессорами
k – адиабатный показатель, определяемый по формуле: k = ср /сV,
где ср – теплоемкость газа при постоянном давлении, сV – теплоемкость газа при постоянном объеме.
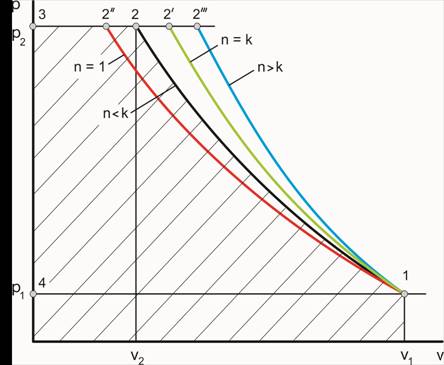
Графически компрессорные процессы изображают на р – v диаграмме, рис. 1.
Рис. 1. р – v диаграммы компрес-сорных процессов, описываемых уравнениями (4…6).
Видео:Курс ""Турбомашины". Раздел 3.1.2. Изменение параметров рабочего процесса в ступени компрессораСкачать
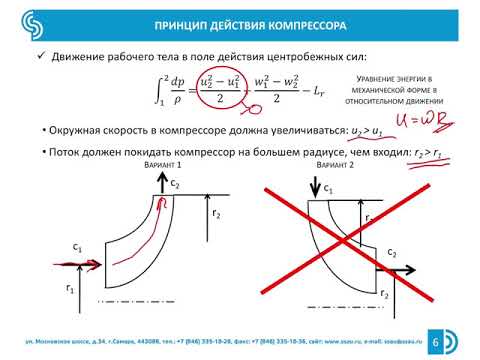
Линиия 1-2 – политропное сжатие при n k.
изоэнтропное сжатие – зеленой линией 1-2΄при n = k;
Политропный процесс при n k (адиабатный) удовлетворительно описывает сжатие в центро-бежных и осевых компрессорах.
Изоэнтропный (S = const,) и изотермический (T = const) процессы (зеленая и красная кривые) неосуществимы. Первый потому, что образование теплоты за счет внутреннего газового тре-ния неизбежно при сжатии газов. Второй – по причине невозможности выполнить конструк-цию системы охлаждения компрессора так, что бы она обеспечивала сжатие с постоянством температуры.
Уравнения энергии компрессорных процессов
Удельная энергия L (Дж/кг), затрачиваемая при сжатии и выталкивании 1 кг воздуха, выража-ется площадью р-v диаграммы, ограниченной изобарами начального р1 и конечного р2 дав-лений, политропой сжатия и осью ординат, рис. 1.
Для процесса с n n = р1v1 n следует:
Так как р1 и v1 – постоянные величины, получим:
Интегрируя выражение (8) в пределах от v1 до v2, получим ﴾ ﴿:
Подставим полученное выражение v1 n в первый член (9):
v2 n /v2 n -1 = v2, так как при делении степени отнимаются. Тоже справедливо для v1 n /v1 n -1 = v1.
Формула (10) примет вид: L = (11)
Сгруппируем члены, содержащие р2v2 и р1v1, получим:
Вернемся к уравнению (1): рv = RT, исходя из которого можно записать:
Заменяя v1 и v2 на полученные выражения, приведем уравнение удельной энергии (12) к виду:
Здесь удельная энергия политропного компрессорного процесса L выражена через универ-сальную газовую постоянную и абсолютные начальную Т1 и конечную Т2 температуры:
Возможна другая форма записи уравнения удельной энергии, через начальное и конечное дав-ление газа: L = (15)
Зная начальные и конечные значения абсолютной температуры (Т1 и Т2) и давления (р1 и р2) можно определить затраты энергии на проведение компрессорного процесса и мощность, потребляемую компрессором:
N = ρQL / ηоηмехηиз, (кг/м 3 × м 3 /с ×Дж/кг = Дж/с = Вт) (16)
где ρ – плотность воздуха, поступающего в компрессор, кг/м 3 ,
Q – объемная подача компрессора, м 3 /с (по условиям всасывания),
L – удельная энергия компрессорного процесса, Дж/кг,
ηо – объемный к. п. д. компрессора,
ηмех – механический к. п. д. компрессора, учитывающий не только собственное трение, но и затраты мощности во вспомогательных механизмах (масляном насосе, вентиляторе, насосе водяного охлаждения и др.),
ηиз – изотермический к. п. д. учитывающий потери мощности на нагревание газа при его сжатии.
Полный к. п. д компрессора равен: η = ηо ηмех ηиз (17)
Площадь фигуры 1-2-3-4 на рис. 1 отражает энергию одного цикла всасывания, сжатия и вы-теснения воздуха: р·v → н/м 2 · м3 = н·м = Дж.
Поршневые компрессоры
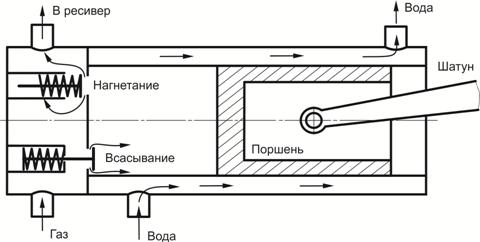
На рис. 2 показана принципиальная схема однопоршневого компрессора.
Видео:Как работает системы рекуперации энергии для компрессоровСкачать
При движении поршня влево, происходит сжатие воздуха, нагнетательный клапан открывает-ся, когда давление в цилиндре сравняется с давлением в ресивере.
При движении поршня вправо, всасывающий клапан открывается, когда давление в цилиндре упадет от уровня давления нагнетания, до давления ниже атмосферного.
Рис. 2. Схема поршневого компрессора
Цилиндры компрессоров выполняют с «мертвым» пространством, чтобы избежать удара поршня о торцевую крышку.
Объем мертвого пространства Vм оценивают в долях рабочего объема Vр цилиндра:
В одноступенчатых компрессорах а = 0,025…0,06 (2,5…6%).
Из-за наличия мертвого пространства всасывание начинается не в начале обратного хода поршня, а в конце процесса расширения.
Во многоступенчатых компрессорах клапаны располагаются на боковых поверхностях ци-линдра и мертвое пространство в них больше: а ≈ 0,2.
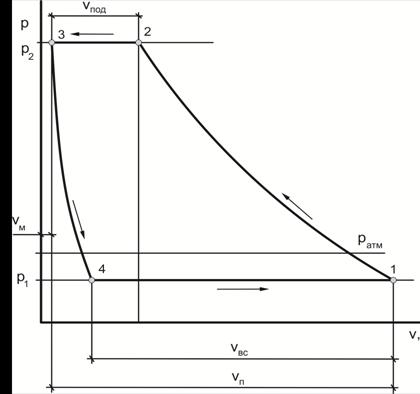
На рис. 3. показана индикаторная диа-грамма компрессора.
Рис. 3. Индикаторная диаграмма поршневого компрессора
Процесс сжатия воздуха изображается линией 1-2 (политропа n = 1,35). Здесь температура воздуха повышается, так как вода не успевает отводить всю теплоту, выделяющуюся при сжатии.
Подача идет по линии 2-3 (изобара), в точке 2 открывается нагнетательный клапан. При постоянном давлении р2 поданный объем газа равен vпод.
Читайте также: Какое масло залить в бежецкий компрессор
Когда поршеньпридет в крайнее левое положение, он вытеснит из цилиндра не весь воздух: его часть Vм «мертвый объем» останется в цилиндре.
В начале хода поршня вправо нагнетательный клапан закроется и остаток воздуха в пространстве Vм будет расширяться по линии 3-4 (политропа n = 1,2). В точке 4 давление станет равным р1 и под действием перепада давлений ратм – р1 через всасывающий клапан поршень начнет всасывать воздух в цилиндр по изобаре 4-1.
Замкнутая фигура 1-2-3-4-1 – это теоретическая индикаторная диаграмма. Действительная ин-дикаторная диаграмма отличается от теоретической в основном в линиях всасывания и по-дачи, так как давление не является строго постоянным (см. индикаторную диаграмму порш-невого насоса).
В поршневых компрессорах в основном применяется водяное охлаждение и, гораздо реже – воздушное. К. п. д. поршневых компрессоров различных конструкций изменяется в пределах от 0,52…0,8.
Отношение всасываемого объема Vвс к рабочему объему цилиндра Vр называется объемным коэффициентом компрессора: λо = Vвс / Vр. (Vвс = λо Vр).
λо – характеризует использование рабочего объема цилиндра.
Действительный объем, всасываемый компрессором отличается от Vвс:
где λт – термический коэффициент, учитывающий нагрев воздуха от стенок цилиндра и его расширение.
Действительная подача по условиям всасывания компрессора одностороннего действия из одного цилиндра равна:
где n – число оборотов вала компрессора, об/мин.
Для современных компрессоров λо = 0,7…0,9; λт = 0,9…0,95.
N = ρQL / ηоηмехηиз, (кг/м 3 × м 3 /с ×Дж/кг = Дж/с = Вт) (16)
где ρ – плотность воздуха, поступающего в компрессор, кг/м 3 ,
Q – объемная подача компрессора, м 3 /с (по условиям всасывания),
Видео:9. ОСНОВЫ ТЕПЛОТЕХНИКИ. ТЕРМОДИНАМИКА КОМПРЕССОРОВ. Работа компрессора. Вредный объём.Скачать
L – удельная энергия компрессорного процесса, Дж/кг,
ηо – объемный к. п. д. компрессора,
ηмех – механический к. п. д. компрессора, учитывающий не только собственное трение, но и затраты мощности во вспомогательных механизмах (масляном насосе, вентиляторе, насосе водяного охлаждения и др.),
ηиз – изотермический к. п. д. учитывающий потери мощности на нагревание газа при его сжатии.
Полный к. п. д компрессора равен: η = ηо ηмех ηиз (17)
Многоступенчатые поршневые компрессоры применяются при степени повышения давления более 150. В них при переходе воздуха из одной ступени в другую его охлаждают в промежуточных охладителях.
На рис. 4 показана схема двухступенчатого компрессора с дифференциальным поршнем.
В крайнем правом положение поршня в штоко-вой полости второй ступени осталось давление Р2, после нагнетания в ресивер.
Рис. 4. Двухступенчатый компрессор.
При движении поршня влево, в первой ступени происходит сжатие воздуха до Р1, которым заполняется охладитель.
Во второй ступени происходит расширение,
Р2снижается, открывается всасывающий клапан и воздух из охладителя заполняет вторую ступень.
Когда Р2 и Р1 сравняются, откроется напорный клапан первой ступени и из нее воздух начнет поступать в охладитель и вторую ступень.
При ходе вправо в первой ступени идет расширение, а когда остаточное давление сравняется с атмосферным – происходит ее заполнение.
Во второй ступени воздух сжимается, а когда давление сравняется с давлением в ресивере, откроется напорный клапан и воздух пойдет в него.
Во многоступенчатых компрессорах объемы ступеней не одинаковы. В каждой последующей ступени он меньше, так как воздух, будучи сжатым, требует меньшего объема. В противном случае, воздух стал бы расширяться, переходя в следующую ступень.
В таких компрессорах процессы сжатия в ступенях осуществляются на разных ходах поршня, поэтому усилия на ходовые части кривошипно-шатунного механизма примерно одинаковые.
Поршневые компрессоры со ступенями сжатия в отдельных цилиндрах
а- с V-образным расположением цилиндров;
б- с прямоугольным расположением цилиндров;
в- с оппозитным расположением цилиндров.
Типы а и б – трудно сбалансировать динамически, поэтому они являются тихоходными:
n = 500…600 об/мин. В них возникают значительные динамические нагрузки, поэтому они требуют массивных фундаментов и, как правило, являются стационарными.
Оппозитные наоборот, из-за симметричности легко балансируются являются быстроходными: n = 1500…2000 об/мин. Их применяют все более широко, но они более габаритны.
Поршневые компрессоры могут развивать давление до 2000 кгс/см 2 при расходе до 2000 м 3 /час.
Дата добавления: 2018-05-12 ; просмотров: 181 ; Мы поможем в написании вашей работы!
- Свежие записи
- Чем отличается двухтактный мотор от четырехтактного
- Сколько масла заливать в редуктор мотоблока
- Какие моторы бывают у стиральных машин
- Какие валы отсутствуют в двухвальной кпп
- Как снять стопорную шайбу с вала
🎦 Видео
Курс ""Турбомашины". Раздел 2.3 Уравнение Бернулли (лектор Батурин О.В.)Скачать
Центробежный компрессорСкачать
Лекция 3 Основы рабочего процесса ВРД. Часть 4 Уравнение сохранения энергии в форме теплосодержанияСкачать
Котика ударило током, 10 т. ВольтСкачать
Закон БернуллиСкачать
Ротационный компрессор; Rotary vane compressorСкачать
Курс ""Турбомашины". Раздел 2.5 Уравнение энергии в тепловой форме (лектор Батурин О.В.)Скачать
Студенты российского вуза разработали вечный двигатель #вечныйдвигатель #изобретенияСкачать
Курс ""Турбомашины". Уравнение количества движенияСкачать
Ременная передача. Урок №3Скачать
Курс ""Турбомашины" Глава 3.2 Рабочий процесс центробежного компрессора. ч. 1 (лектор Батурин О.В.)Скачать
Энергия заряженного конденсатораСкачать
Курс ""Турбомашины". Раздел 7.1 Диаграмма Смита для компрессора (лектор Батурин О.В.)Скачать
Тепло компрессорных установок / Тепловыделение компрессора, рекуперация теплаСкачать
Курс ""Турбомашины". Раздел 7.8 Зачем и как регулировать многоступенчатые компрессоры (Батурин О.В.)Скачать
