Для определения работы, затрачиваемой на сжатие воздуху в компрессоре и установления связи между параметрами воздуха при его перетекании по элементам проточной части, воспользуемся уравнениями сохранения энергии и Бернулли.
Применительно к компрессору уравнение сохранения энергии можно записать в следующем виде:
| где | — кинетическая энергия 1 кг воздуха на входе в компрессор; |
| — энергия, эквивалентная теплосодержанию 1 кг воздуха на входе в компрессор; | |
| — энергия, сообщаемая 1 кг воздуха в виде механической работы колеса (внутренняя работа сжатия); | |
| — энергия, сообщаемая 1 кг воздуха в виде тепла, которое передается воздуху через стенки компрессора. Вследствие малости величины ею пренебрегают и в дальнейшем этот член уравнения (8.2) не учитывается; | |
| — энергия, эквивалентная теплосодержанию 1 кг воздуха на выходе из компрессора; | |
| — кинетическая энергия 1 кг воздуха на выходе из компрессора. Параметры воздуха на входе в компрессор отмечены индексом «1», на выходе из компрессора – индексом «к». |
Применительно к воздуху принимается: показатель адиабаты сжатия k = 1,4
Из (8.2) следует, что сумма полной энергии воздуха на входе в компрессор и подведенной работы LK равна полной энергии воздуха на выходе из компрессора.
Полная энергия воздуха складывается из кинетической энергии и теплосодержания. Уравнение (8.2) можно представить в другом виде:
Из (8.3) следует, что работа компрессора затрачивается на увеличение кинетической энергии и теплосодержания воздуха. В диффузоре 3 и выходном устройстве 4 (см. рис. 8.2) скорость воздуха уменьшается; обычно скорость с4 на выходе из компрессора мало отличается от скорости с1 на входе в рабочее колесо.
Если пренебречь разностью скоростей воздуха на выходе и на входе и принять с4 = с1 то
т.е. вся подведенная к компрессору работа расходуется на увеличение теплосодержания воздуха. Величина разности ТК.-Т1 характеризует подогрев воздуха в компрессоре.
Видео:Как нарушить закон сохранения энергии?Скачать
Считая процесс сжатия воздуха в компрессоре политропным, можно написать уравнение политропы в виде
Подставив (8.6) в (8.4), получим
Показатель политропы п тем больше, чем больше потери энергии при сжатии. Показатель адиабаты k = 1,4 в уравнении (8.7) характеризует теплоемкость воздуха, но не означает, что сжатие происходит без тепловых потерь. В уравнениях (8.2) — (8.4) потери на трение воздуха (гидравлические потери) в явном виде не выражены; в действительности же они учтены величиной температуры Тк, так как работа сил трения превращается в тепло.
Уравнение Бернулли применительно к процессу сжатия воздуха в компрессоре устанавливает, что подведенная к компрессору работа LK расходуется на сжатие воздуха LПК, преодоление гидравлических потерь LrK и изменение кинетической энергии
Читайте также: Датчик давления компрессора авто
Политропная работа сжатия выражается зависимостью
Из сопоставления (8.9) и (8.7) видно, что
Политропная работа может оказаться равной внутренней работе лишь в случае адиабатного сжатия, т.е. когда п = k и потери отсутствуют. Известно, что реальное сжатие всегда сопровождается потерями, а наличие потерь приводит к повышению температуры воздуха в соответствующих сечениях компрессора. Из (8.7) и (8.8) следует, что работа, затрачиваемая на сжатие 1 кг воздуха, пропорциональна температуре Т1. Объясняется это тем, что при равных давлениях удельный объем воздуха тем больше, чем больше Т1. Таким образом, чем больше температура воздуха и гидравлические потери в элементах компрессора, тем большую энергию нужно затратить для сжатия до данного давления.
Видео:1.3.5 Закон сохранения энергии и превращения механической энергииСкачать
Гидравлические потери увеличивают работу, которую необходимо подвести к компрессору, на величину LrK; наряду с этим, наличие потерь вызывает подогрев воздуха и увеличение вследствие этого самой политропной работы LПK.
Рассмотренные зависимости справедливы не только для центробежных компрессоров, но и для любых компрессорных машин, независимо от особенностей их конструкции.
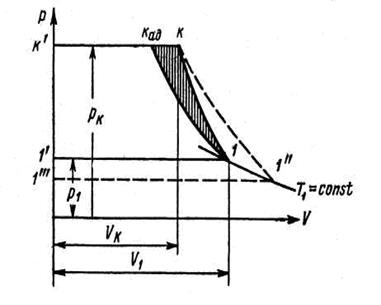
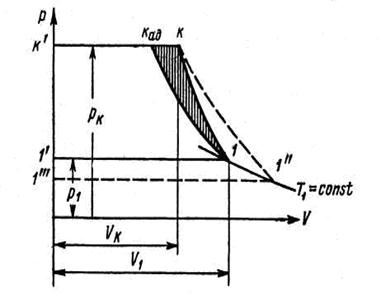
Графическая интерпретация уравнения Бернулли представлена на рис. 8.5, который дает наглядное представление о процессе сжатия в компрессоре. По оси ординат отложено давление р, по оси абсцисс — удельный объем . Точка 1 (p1, v1) характеризует состояние воздуха на входе в рабочее колесо компрессора. Точка К (рк, Vk) характеризует состояние воздуха на выходе из компрессора. Линия 1-Кад есть адиабата сжатия; линия 1—К представляет собой политропу сжатия. Чем больше потери в компрессоре, тем более отклоняется политропа от идеального сжатия без потерь по адиабате. Площадь слева от линии процесса характеризует работу сжатия.
Из графика видно, что политропная работа LПK = пл. 1—К—К’—1’—1 больше адиабатной работы Lад = пл. 1—Кал—К’—1’—1 на величину заштрихованной площадки. Если через точку 1 провести изотерму Т1 = const, а из точки К, характеризующей состояние воздуха на выходе из компрессора при политропном сжатии, провести адиабату К—1″ до пересечения с изотермой Т1 = const, то площадка, заключенная между пунктирными линиями и линиями К—1—1′, будет соответствовать работе трения компрессора. Площадь диаграммы слева от линии К—1″ представляет собой сумму политропной работы сжатия LПK и работы сил трения Lrк, т.е. работу компрессора LK.
Факторы, влияющие на мощность, затрачиваемую на привод компрессора
Тема 2.3 Потери энергии при работе компрессора.
Читайте также: Замена внутреннего подшипника компрессора кондиционера фф2
Видео:Галилео. Эксперимент. Закон сохранения энергииСкачать
1. Факторы, влияющие на мощность, затрачиваемую на привод компрессора.
2. Адиабатный к.п.д. компрессора.
Для определения работы, затрачиваемой на сжатие воздуху в компрессоре и установления связи между параметрами воздуха при его перетекании по элементам проточной части, воспользуемся уравнениями сохранения энергии и Бернулли.
Применительно к компрессору уравнение сохранения энергии можно записать в следующем виде:
| — кинетическая энергия 1 кг воздуха на входе в компрессор; |
| — энергия, эквивалентная теплосодержанию 1 кг воздуха на входе в компрессор; |
| — энергия, сообщаемая 1 кг воздуха в виде механической работы колеса (внутренняя работа сжатия); |
| — энергия, сообщаемая 1 кг воздуха в виде тепла, которое передается воздуху через стенки компрессора. Вследствие малости величины ею пренебрегают и в дальнейшем этот член уравнения (8.2) не учитывается; |
| — энергия, эквивалентная теплосодержанию 1 кг воздуха на выходе из компрессора; |
| — кинетическая энергия 1 кг воздуха на выходе из компрессора. Параметры воздуха на входе в компрессор отмечены индексом «1», на выходе из компрессора – индексом «к». |
Применительно к воздуху принимается: показатель адиабаты сжатия k = 1,4
Из (8.2) следует, что сумма полной энергии воздуха на входе в компрессор и подведенной работы LK равна полной энергии воздуха на выходе из компрессора.
Полная энергия воздуха складывается из кинетической энергии и теплосодержания. Уравнение (8.2) можно представить в другом виде:
Из (8.3) следует, что работа компрессора затрачивается на увеличение кинетической энергии и теплосодержания воздуха. В диффузоре 3 и выходном устройстве 4 (см. рис. 8.2) скорость воздуха уменьшается; обычно скорость с4 на выходе из компрессора мало отличается от скорости с1 на входе в рабочее колесо.
Если пренебречь разностью скоростей воздуха на выходе и на входе и принять с4 = с1 то
Видео:ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ в механике класс физика ПерышкинСкачать
т.е. вся подведенная к компрессору работа расходуется на увеличение теплосодержания воздуха. Величина разности ТК.-Т1 характеризует подогрев воздуха в компрессоре.
Считая процесс сжатия воздуха в компрессоре политропным, можно написать уравнение политропы в виде
Подставив (8.6) в (8.4), получим
Показатель политропы п тем больше, чем больше потери энергии при сжатии. Показатель адиабаты k = 1,4 в уравнении (8.7) характеризует теплоемкость воздуха, но не означает, что сжатие происходит без тепловых потерь. В уравнениях (8.2) — (8.4) потери на трение воздуха (гидравлические потери) в явном виде не выражены; в действительности же они учтены величиной температуры Тк, так как работа сил трения превращается в тепло.
Уравнение Бернулли применительно к процессу сжатия воздуха в компрессоре устанавливает, что подведенная к компрессору работа LK расходуется на сжатие воздуха LПК, преодоление гидравлических потерь LrK и изменение кинетической энергии
Читайте также: Сравнение компрессоров для кондиционеров
Политропная работа сжатия выражается зависимостью
Из сопоставления (8.9) и (8.7) видно, что
Видео:Закон Сохранения Энергии // Урок по Физике 7 класс - Закон Сохранения Механической ЭнергииСкачать
Политропная работа может оказаться равной внутренней работе лишь в случае адиабатного сжатия, т.е. когда п = k и потери отсутствуют. Известно, что реальное сжатие всегда сопровождается потерями, а наличие потерь приводит к повышению температуры воздуха в соответствующих сечениях компрессора. Из (8.7) и (8.8) следует, что работа, затрачиваемая на сжатие 1 кг воздуха, пропорциональна температуре Т1. Объясняется это тем, что при равных давлениях удельный объем воздуха тем больше, чем больше Т1. Таким образом, чем больше температура воздуха и гидравлические потери в элементах компрессора, тем большую энергию нужно затратить для сжатия до данного давления.
Гидравлические потери увеличивают работу, которую необходимо подвести к компрессору, на величину LrK; наряду с этим, наличие потерь вызывает подогрев воздуха и увеличение вследствие этого самой политропной работы LПK.
Рассмотренные зависимости справедливы не только для центробежных компрессоров, но и для любых компрессорных машин, независимо от особенностей их конструкции.
Графическая интерпретация уравнения Бернулли представлена на рис. 8.5, который дает наглядное представление о процессе сжатия в компрессоре. По оси ординат отложено давление р, по оси абсцисс — удельный объем . Точка 1 (p1, v1) характеризует состояние воздуха на входе в рабочее колесо компрессора. Точка К (рк, Vk) характеризует состояние воздуха на выходе из компрессора. Линия 1-Кад есть адиабата сжатия; линия 1—К представляет собой политропу сжатия. Чем больше потери в компрессоре, тем более отклоняется политропа от идеального сжатия без потерь по адиабате. Площадь слева от линии процесса характеризует работу сжатия.
Из графика видно, что политропная работа LПK = пл. 1—К—К’—1’—1 больше адиабатной работы Lад = пл. 1—Кал—К’—1’—1 на величину заштрихованной площадки. Если через точку 1 провести изотерму Т1 = const, а из точки К, характеризующей состояние воздуха на выходе из компрессора при политропном сжатии, провести адиабату К—1″ до пересечения с изотермой Т1 = const, то площадка, заключенная между пунктирными линиями и линиями К—1—1′, будет соответствовать работе трения компрессора. Площадь диаграммы слева от линии К—1″ представляет собой сумму политропной работы сжатия LПK и работы сил трения Lrк, т.е. работу компрессора LK.
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
- Свежие записи
- Чем отличается двухтактный мотор от четырехтактного
- Сколько масла заливать в редуктор мотоблока
- Какие моторы бывают у стиральных машин
- Какие валы отсутствуют в двухвальной кпп
- Как снять стопорную шайбу с вала
Видео:Физика 10 Закон сохранения энергии в механикеСкачать
🌟 Видео
закон сохранения энергииСкачать
УДОВОЛЬСТВИЕ ОТ ГРЕХА И ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ. Протоиерей Александр ТылькевичСкачать
Закон сохранения энергии в колебательном контуреСкачать
Закон сохранения энергии / Law of energy conservationСкачать
Закон сохранения энергии в механике | Физика 10 класс #21 | ИнфоурокСкачать
Лекция 3 Основы рабочего процесса ВРД. Часть 4 Уравнение сохранения энергии в форме теплосодержанияСкачать
ФИЗИКА 10 класс: Закон сохранения энергииСкачать
Закон сохранения энергии | Образовательный семинар доктора БожьеваСкачать
Физика - импульс и закон сохранения импульсаСкачать
Закон сохранения импульсаСкачать
Закон сохранения превращения энергии в тепловых процессах. 8 класс.Скачать
8 класс, 7 урок, Закон сохранения энергии в тепловых процессахСкачать
Физика # 8. Механика. Закон сохранения энергии. Что храним?Скачать
Вселенная нарушает закон сохранения энергииСкачать
