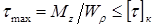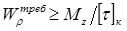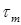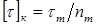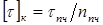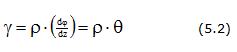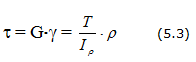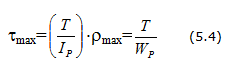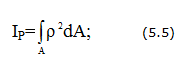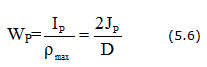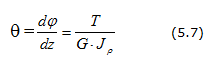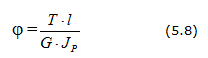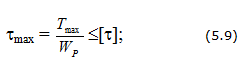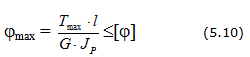Условие прочности при кручении валов

Условие прочности бруса при кручении заключается в том, что наибольшее касательное напряжение, возникающее в нем, не должно превышать предельно допустимое. При этом расчетная формула на прочность имеет вид:

где [τ_кр] — предельное допускаемое напряжение.

При практических расчетах, определяя предельные допускаемые напряжения для различных материалов, используют зависимость между напряжениями при растяжении и напряжениями при кручении, которая для стали и чугуна имеет вид:

(здесь [σ_р] — справочная или определяемая экспериментально величина, (предельное допустимое напряжение растяжения) характеризующая материал бруса (вала).

Кроме требования прочности к валам предъявляются требования жесткости, которое заключается в том, что угол закручивания участка вала длиной 1 м не должен превышать предельной величины, определяемой требованиями конструкции. Допускаемый угол закручивания 1 м длины вала задается в градусах и обозначается [φ₀°] .
Расчетная формула на жесткость при кручении имеет вид:

В реальных механизмах обычно допускаются углы закручивания валов в пределах [φ₀°] = 0,25. 1 градус/м.

Пример решения задачи на кручение

Определить минимальный допустимый диаметр вала d , передающего крутящий момент М_кр = 464 Нм, если допускаемое напряжение кручения [τ_кр] = 30 МПа.

Решение

По известному передаваемому крутящему моменту можно определить момент сопротивления кручению:

W_r = М_кр / [τ_кр] = 464 / 30 х 10 6 = 15,6 х 10 -6 м 3 .

Из зависимости между моментом сопротивления кручению и диаметром вала W_r ≈ 0,2D 3 находим минимальный допустимый диаметр:

D ≈ 3 √( W_r / 0,02) ≈ 43 мм (здесь и далее √ — знак корня).

Округляя найденное значение диаметра до стандартной величины (в большую сторону), принимаем D = 45 мм.

Потенциальная энергия деформации при кручении

Представим себе круглый цилиндрический брус (вал) постоянного сечения, жестко защемленный одним концом и нагруженный на другом конце моментом, приложенным статически, т. е. медленно возрастающим от нуля до какого-либо значения Т .
Полагаем, что момент остается в пределах, когда нагрузка и деформация пропорциональны, т. е. справедлив закон Гука.

Момент Т вызывает в брусе деформацию кручения и при этом совершает работу W , которая аккумулируется в виде потенциальной энергии деформации U , причем пренебрегая незначительными потерями энергии (например, на нагрев бруса), можно считать, что W = U .

Работа в случае статического нагружения равна: W = Т φ / 2 , где φ — полный угол закручивания бруса.
Так как Т = М_кр , то справедливо равенство:

U = W = Т φ / 2 = М_кр 2 l / (2Gl_r) .

При одновременном действии нескольких моментов или ступенчатом изменении размеров поперечного сечения брус разбивают на однородные участки и потенциальную энергию деформации всего бруса определяют как сумму потенциальных энергий этих участков.

Читайте также: Подшипник приводного вала вольво s80

Материалы раздела «Деформация кручения»:

Видео:Кручение. Часть 5 Условие прочностиСкачать

Условие прочности при кручении

Условие прочности при кручении: прочность вала считается обеспеченной, если наибольшие касательные напряжения, возникающие в его опасном поперечном сечении, не превышают допускаемых напряжений на кручение :

Формула служит для проверочного расчета вала на прочность.

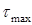
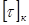
Допускается незначительное (до 5 %) превышение расчетного напряжения над допускаемым напряжением .

При проектировочном расчете требуемый полярный момент сопротивления определяется по формуле условия прочности при кручении :

.

Для вала постоянного диаметра опасным сечением при кручении является сечение, в котором возникает наибольший крутящий момент. Если сечение вала не постоянно по длине, может оказаться, что наибольшие касательные напряжения возникают не там, где крутящий момент максимален. Следовательно, в этом случае вопрос об опасном сечении должен быть исследован дополнительно.

Допускаемое напряжение :

для пластичных материалов назначается в зависимости от предела текучести () при кручении (сдвиге):

.

для хрупких материалов назначается в зависимости от предела прочности:

.

Видео:КРУЧЕНИЕ ВАЛА. Касательные напряжения. Сопромат.Скачать

iSopromat.ru

Для обеспечения прочности и жесткости вала при кручении, напряжения и деформации от крутящих моментов не должны превышать соответствующих допустимых значений.

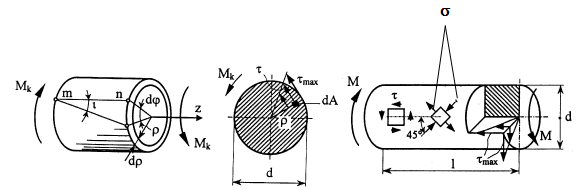
Этот вид нагружения возникает при приложении к брусу пар сил, плоскости действия которых перпендикулярны его оси. Такие брусья принято называть валами.

Внешние пары, приложенные к валу, будем называть скручивающими моментами. Они могут быть сосредоточенными М₁, М₂, …, М_n или распределенными m по длине вала l .

Крутящий момент является равнодействующим моментом напряжений, возникающих в каком-либо сечении вала относительно его продольной оси.

Видео:Вал. Расчет на прочность при косом изгибе и крученииСкачать

Внутренний крутящий момент

При определении величины крутящего момента используется метод сечений. Суть его заключается в следующем: рассекаем вал сечением и отбрасываем одну из частей вала, расположенную либо справа, либо слева от сечения.

Обычно отбрасывают ту часть, к которой приложено больше скручивающих пар. Действие отброшенной части на рассматриваемую заменяют внутренним силовым фактором – крутящим моментом T . Затем из условий равновесия остановленной части вала определяют крутящий момент:

Таким образом, крутящий момент в каком либо сечении вала является уравновешивающей парой сил всех внешних скручивающих пар, приложенных либо слева, либо справа от рассматриваемого сечения.

Видео:Сопротивление материалов. Лекция: расчёт на прочность при крученииСкачать

Напряжения при кручении

Распределение касательных напряжений

Максимальное касательное напряжение

Геометрические характеристики круглых сплошных сечений вала

Полярный момент сопротивления

Видео:12. Подбор сечения при кручении ( практический курс по сопромату )Скачать

Деформации вала

Видео:Статически неопределимый вал. Расчет на прочность при крученииСкачать

Условия прочности и жесткости вала

Расчет вала при кручении сводится к одновременному удовлетворению двух условий:

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Читайте также: Подшипник второй передачи вторичного вала кпп фотон 1093

Видео:Сопромат. Практическое занятие №1.4Скачать

Решение задач, контрольных и РГР

Стоимость мы сообщим в течение 5 минут
на указанный вами адрес электронной почты.

Если стоимость устроит вы сможете оформить заказ.

Видео:Расчет вала на прочность и жесткость. Эпюра крутящих моментовСкачать

Набор студента для учёбы

— Рамки A4 для учебных работ
— Миллиметровки разного цвета
— Шрифты чертежные ГОСТ
— Листы в клетку и в линейку

Видео:Кручение валаСкачать

Условие прочности при кручении вала

При расчете на прочность при кручении необходимо знать максимальные напряжения для сравнения их с допускаемыми напряжениями. Очевидно, что максимальные напряжения при кручении круглого вала будут иметь точки максимально удаленные от оси вала. Т.е. точки с полярной координатой, равной радиусу сечения вала r:

Отношение полярного момента инерции J_r к наибольшему радиусу сечения r называется полярным моментом сопротивления W_r:

Тогда условие прочности при кручении будет иметь следующий вид:

Для сплошного круглого сечения:

Как следует из закона парности касательных напряжений, одновременно с касательными напряжениями, действующими в плоскости поперечного сечения вала, имеют место касательные напряжения в продольных плоскостях. Они равны по величине парным напряжениям, но имеют противоположный знак. Таким образом, все элементы бруса при кручении находятся в состоянии чистого сдвига. Так как чистый сдвиг является частным случаем плоского напряженного состояния, при котором то при повороте граней элемента на 45° в новых площадках обнаруживаются только нормальные напряжения, равные по величине t (рис. 6.7).

Рассмотрим возможные виды разрушения валов, изготовленных из различных материалов при кручении. Валы из пластичных материалов чаще всего разрушаются по сечению, перпендикулярному к оси вала, под действием касательных напряжений, действующих в этом сечении (рис. 6.8,а). Валы из хрупких материалов, разрушаются по винтовой поверхности наклоненной к оси вала под углом 45°, т.е. по направлению действия максимальных растягивающих напряжений (рис. 6.8,б). У деревянных валов первые трещины возникают по образующим цилиндра, так как древесина плохо сопротивляется действию касательных напряжений, направленных вдоль волокон (рис. 6.8,в).

Таким образом, характер разрушения зависит от способности материала вала сопротивляться воздействию нормальных и касательных напряжений. В соответствии с этим, допускаемые касательные напряжения принимаются равным [t] = [s_р] — для хрупких материалов и [t] = (0,5¸0,6)[s] — для пластичных материалов.

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Видео:Кручение. Часть 6 Жесткость валаСкачать

Тема 2.4. Кручение

Под кручением понимается такой вид деформации, когда в поперечных сечениях бруса действует только крутящий момент M_k, (другое обозначение T, M_z), а остальные силовые факторы (нормальная и поперечная силы и изгибающие моменты) отсутствуют.

Читайте также: Датчик положения коленчатого вала renault megane

Или другое определение кручением называют деформацию, возникающую при действии на стержень пары сил, расположенной в плоскости, перпендикулярной к его оси (рис.1).

Кручение возникает в валах, винтовых пружинах, в элементах пространственных конструкций и т.п.

Деформация кручения наблюдается если прямой брус нагружен внешними моментами (парами сил M), плоскости действия которых перпендикулярны к его продольной оси

В чистом виде деформация кручения встречается редко, обычно присутствуют и другие внутренние силовые факторы (изгибающие моменты, продольные силы).

Стержни круглого или кольцевого сечения, работающие на кручение, называют валами.

Внешние крутящие моменты передаются на вал в местах посадки на него шкивов, зубчатых колес, там, где поперечная нагрузка смещена относительно оси вала.

Мы будем рассматривать прямой брус только в состоянии покоя или равномерного вращения. В этом случае алгебраическая сумма всех внешних скручивающих моментов, приложенных к брусу, будет равна нулю.

При расчете брусьев, испытывающий деформацию кручения, на прочность и жесткость при статическом действии нагрузки, надо решить две основные задачи. Это определение напряжений (от M_k), возникающих в брусе, и нахождение угловых перемещений в зависимости от внешних скручивающих моментов.

При расчете валов обычно бывает известна мощность, передаваемая на вал, а величины внешних скручивающих моментов, подлежат определению. Внешние скручивающие моменты, как правило, передаются на вал в местах посадки на него шкивов, зубчатых колес и т.п.

В ряде случаев величины внешних крутящих моментов определяются по величине потребляемой мощности и по скорости вращения вала. Если вал делает в минуту n оборотов (n- частота вращения, единицы измерения — об/мин.), то вращающий момент можно найти по формуле: М_вр=P/n,

эта формула дает значение момента в Н·м, если мощность выражена в Вт, а частота вращения n — об/мин.

§2. Построение эпюр крутящих моментов

Для определения напряжений и деформаций вала необходимо знать значения внутренних крутящих моментов M_k (M_z) в поперечных сечениях по длине вала. Диаграмму, показывающую распределение значений крутящих моментов по длине бруса, называют эпюрой крутящих моментов. Зная величины внешних скручивающих моментов и используя метод сечений, мы можем определить крутящие моменты, возникающие в поперечных сечениях вала.

В простейшем случае, когда вал нагружен только двумя внешними моментами (эти моменты из условия равновесия вала ΣM_z=0 всегда равны друг другу по величине и направлены в противоположные стороны), как показано на рис. 1, крутящий момент M_z в любом поперечном сечении вала (на участке между внешними моментами) по величине равен внешнему моменту |M₁|=|M₂|.

• Свежие записи
  • Чем отличается двухтактный мотор от четырехтактного
  • Сколько масла заливать в редуктор мотоблока
  • Какие моторы бывают у стиральных машин
  • Какие валы отсутствуют в двухвальной кпп
  • Как снять стопорную шайбу с вала

  
  

  источники:

  https://evakuatorinfo.ru/uslovie-prochnosti-pri-kruchenii-valov

  💡 Видео

  11. Кручение ( практический курс по сопромату )Скачать

  

  Правило знаков при крученииСкачать

  

  Изгиб с кручением. Расчет на прочностьСкачать

  

  Изгиб с кручениемСкачать

  

  Расчет вала на изгиб с кручениемСкачать

  

  Сопромат. Построение эпюр вала при кручении. Я в вк https://vk.com/id4682924Скачать

  

  Кручение зажатого валаСкачать

  

  КРУЧЕНИЕ. ЭПЮРЫ ЗАКРУЧИВАНИЯ. Углы поворота. СопроматСкачать

  

  Прочность и жесткость валов. Часть 9. Расчет на жесткость промежуточного вала (КЦ-редуктор)Скачать