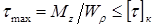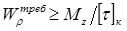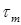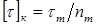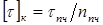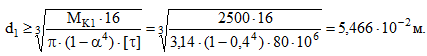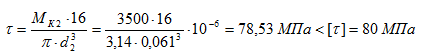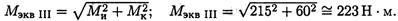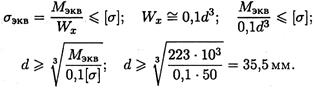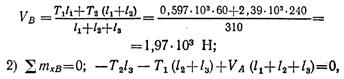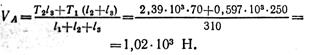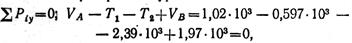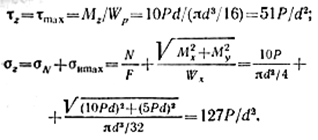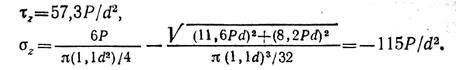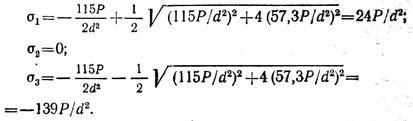Условие прочности вала диаметром d по касательным напряжениям

Условие прочности при кручении: прочность вала считается обеспеченной, если наибольшие касательные напряжения, возникающие в его опасном поперечном сечении, не превышают допускаемых напряжений на кручение :

Формула служит для проверочного расчета вала на прочность.

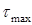
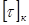
Допускается незначительное (до 5 %) превышение расчетного напряжения над допускаемым напряжением .

При проектировочном расчете требуемый полярный момент сопротивления определяется по формуле условия прочности при кручении :

.

Для вала постоянного диаметра опасным сечением при кручении является сечение, в котором возникает наибольший крутящий момент. Если сечение вала не постоянно по длине, может оказаться, что наибольшие касательные напряжения возникают не там, где крутящий момент максимален. Следовательно, в этом случае вопрос об опасном сечении должен быть исследован дополнительно.

Допускаемое напряжение :

для пластичных материалов назначается в зависимости от предела текучести () при кручении (сдвиге):

.

для хрупких материалов назначается в зависимости от предела прочности:

.

Видео:КРУЧЕНИЕ ВАЛА. Касательные напряжения. Сопромат.Скачать

iSopromat.ru

Пример решения задачи по расчету (и подбору по ГОСТ) диаметров поперечного сечения вала нагруженного крутящими моментами по условию прочности при кручении.

Видео:ПОДБОР ДВУТАВРА И ШВЕЛЛЕРА. Проверка прочности балки. Сопромат.Скачать

Задача

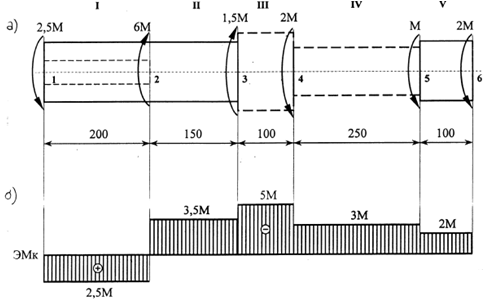
Подобрать размеры поперечного сечения вала (рис. 1) по условию прочности. На участках от сечения 1 до сечения 3 и от сечения 5 до сечения 6 наружный диаметр вала по конструктивным соображениям должен иметь одинаковый размер.

На участке от сечения 1 до сечения 2 вал кольцевого поперечного сечения с n=d_B/d=0,4. На участках от сечения 3 до сечения 5 вал подбирается только по условию прочности.

Видео:Понимание напряжений в балкахСкачать

Решение

Разбиваем вал на силовые участки, строим эпюру крутящего момента (рис. 1,б).

Определяем диаметры вала. На I, II и V участках наружный диаметр вала одинаков. Для них не возможно заранее указать сечение с наибольшим значением касательного напряжения, так как различные участки имеют различные типы поперечного сечения: I участок – кольцевое, II и V – сплошное круглое.

Приходится определять отдельно по условию прочности диаметры для каждого типа поперечного сечения по наиболее нагруженному силовому участку (то есть тому, на котором действует максимальный по абсолютной величине крутящий момент). Окончательно примем наибольший полученный диаметр.

Для участка с кольцевым сечением:

Для вала сплошного поперечного сечения

Окончательно принимаем наибольшее значение полученного диаметра, округленное до целого значения в большую сторону:

Наибольшее действующее на этих участках напряжение:

Диаметр вала на III участке (М_К3 = 5М = 5 кНм):

Аналогично диаметр вала на IV участке М_К4=3М=3 кНм.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Видео:РАСТЯЖЕНИЕ-СЖАТИЕ. Построение эпюр. Сопромат.Скачать

Решение задач, контрольных и РГР

Стоимость мы сообщим в течение 5 минут
на указанный вами адрес электронной почты.

Если стоимость устроит вы сможете оформить заказ.

Видео:Расчет вала на прочность и жесткость. Эпюра крутящих моментовСкачать

Набор студента для учёбы

— Рамки A4 для учебных работ
— Миллиметровки разного цвета
— Шрифты чертежные ГОСТ
— Листы в клетку и в линейку

Видео:Статически неопределимый вал. Расчет на прочность при крученииСкачать

Особенность расчета валов

Большинство валов испытывают сочетание деформаций изгиба и кручения. Обычно валы — прямые брусья с круглым или кольце­вым сечением. При расчете валов касательные напряжения от дей­ствия поперечных сил не учитывают из-за их незначительности.

Расчеты проводят по опасным поперечным сечениям. При про­странственном нагружении вала пользуются гипотезой независимо­сти действия сил и изгибающие моменты рассматривают в двух вза­имно перпендикулярных плоскостях, а суммарный изгибающий мо­мент определяют геометрическим суммированием.

Примеры решения задач

Пример 1. В опасном поперечном сечении круглого бруса воз­никают внутренние силовые факторы (рис. 35.1) М_х; М_у; M_z.

М_х и М_у — изгибающие моменты в плоскостях уОх и zOx со­ответственно; M_z — крутящий момент. Проверить прочность по ги­потезе наибольших касательных напряжений, если [σ] = 120 МПа. Исходные данные: М_х = 0,9 кН • м; М_у = 0,8 кН • м; M_z = 2,2 кН*м; d = 60 мм.

Читайте также: Паровые компрессоры служат для повышения давления пара

Строим эпюры нормальных напряжений от действия изгибаю­щих моментов относительно осей Ох и Оу и эпюру касательных на­пряжений от кручения (рис. 35.2).

Максимальное касательное напряжение возникает на поверхно­сти. Максимальные нормальные напряжения от момента М_х возни­кают в точке А, максимальные нормальные напряжения от момента М_у в точке В. Нормальные напряжения складываются, потому что изгибающие моменты во взаимно перпендикулярных плоскостях гео­метрически суммируются.

Суммарный изгибающий момент:

Рассчитываем эквивалентный момент по теории максимальных касательных напряжений:

Момент сопротивления сечения: W_oceвoe = 0,1 • 60 3 = 21600мм 3 .

Пример 2. Из условия прочности рассчитать необходимый диа­метр вала. На валу установлены два колеса. На колеса действуют две окружные силы F_t1 = 1,2кН; F_t2 = 2кН и две радиальные силы в вертикальной плоскости F_r1 = 0,43кН; F_r2 = 0,72кН (рис. 35.3). Диаметры колес соответственно равны d₁ = 0,1м; d₂ = 0,06 м.

Принять для материала вала [σ] = 50МПа.

Рассчитать размеры вала кольцевого сечения при с = 0,8 (с = d_вн / d).

Расчет провести по гипотезе максимальных каса­тельных напряжений. Весом вала и колес пренебречь.

Указание. Используем принцип независимости действия сил, составляем расчетные схемы вала в вертикальной и горизонтальной плоскостях. Определяем реакции в опорах в горизонтальной и вертикальной плоскостях в отдельности. Строим эпюры изгиба­ющих моментов (рис. 35.4). Под действием окружных сил вал скручивается. Определяем действующий на валу крутящий момент.

Составим расчетную схему вала (рис. 35.4).

1. Крутящий момент на валу:

2. Изгиб рассматриваем в двух плоскостях: горизонтальной (пл. Н) и вертикальной (пл. V).

В горизонтальной плоскости определяем реакции в опоре:

Определяем изгибающие моменты в точках С и В:

В вертикальной плоскости определяем реакции в опоре:

Определяем изгибающие моменты в точках С и В:

Суммарные изгибающие моменты в точках С и В:

В точке В максимальный изгибающий момент, здесь же дей­ствует и крутящий момент.

Расчет диаметра вала ведем по наиболее нагруженному сечению.

3. Эквивалентный момент в точке В по третьей теории прочности

4. Определяем диаметр вала круглого поперечного сечения из условия прочности

Округляем полученную величину: d = 36 мм.

Примечание. При выборе диаметров вала пользоваться стандартным рядом диаметров (Приложение 2).

5. Определяем необходимые размеры вала кольцевого сечения при с = 0,8, где d — наружный диаметр вала.

Диаметр вала кольцевого сечения можно определить по форму­ле

Перегрузка незначительная. d_BH = 0,8d = 0,8 • 42 = 33,6мм.

Округляем до значения d_BH = 33 мм.

6. Сравним затраты металла по площадям сечения вала в обоих случаях.

Площадь поперечного сечения сплошного вала

Площадь поперечного сечения полого вала

Площадь поперечного сечения сплошного вала почти в два раза больше вала кольцевого сечения:

Пример 3. Определить размеры поперечного се­чения вала (рис. 2.70, а) привода управления. Усилие от тяги педали P₃, усилия, передаваемые механизмом P₁, Р₂, Р₄. Материал вала — сталь СтЗ с пределом те­кучести σ_т = 240 Н/мм 2 , требуемый коэффициент запаса [n] = 2,5. Расчет выполнить по гипотезе энергии формо­изменения.

Рассмотрим равновесие вала, предварительно приведя силы Р₁, Р₂, Р₃, Р₄ к точкам, лежащим на его оси.

Перенося силы Р₁ параллельно самим себе в точки К и E, надо добавить пары сил с моментами, равными моментам сил Р₁ относительно точек К и Е, т. е.

Эти пары сил (моменты) условно показаны на рис. 2.70, б в виде дугообразных линий со стрелками. Аналогично при переносе сил Р₂, Р₃, Р₄ в точки K, E, L, Н надо добавить пары сил с моментами

Опоры вала, изображенного на рис. 2.70, а, надо рассматривать как пространственные шарнирные опоры, препятствующие перемещениям в направлении осей х и у (выбранная система координат показана на рис. 2.70, б).

Пользуясь расчетной схемой, изображенной на рис. 2.70, в, составим уравнения равновесия:

Составим проверочное уравнение:

следовательно, опорные реакции Н_А и Н_В определены верно.

Читайте также: Ремонт компрессоров для подкачки шин в саратове

Эпюры крутящих моментов М_z и изгибающих момен­тов М_у представлены на рис. 2.70, г. Опасным является сечение слева от точки L.

Условие прочности имеет вид:

где эквивалентный момент по гипотезе энергии формо­изменения

Требуемый наружный диаметр вала

Принимаем d = 45 мм, тогда d₀ = 0,8 _* 45=36 мм.

Пример 4. Проверить прочность промежуточного вала (рис. 2.71) цилиндрического прямозубого редуктора, если вал передает мощность N = 12,2 кВт при частоте вращения п = 355 об/мин. Вал изготовлен из стали Ст5 с пределом текучести σ_т = 280 Н/мм 2 . Требуемый коэф­фициент запаса [n] = 4. При расчете применить гипотезу наибольших касательных напряжений.

Указание. Окружные усилия Р₁ и Р₂ лежат в горизонталь­ной плоскости и направлены по касательным к окружностям зубчатых колес. Радиальные усилия T₁ и Т₂ лежат в верти­кальной плоскости и выражаются через соответствующее окружное усилие следующим образом: T = 0,364Р.

На рис. 2.71, а представлен схематический чертеж вала; на рис. 2.71, б показана схема вала и усилия, возникающие в зубчатом зацеплении.

Определим момент, передаваемый валом:

Очевидно, m = m₁ = m₂ (скручивающие моменты, приложен­ные к валу, при равномерном вращении равны по вели­чине и противоположны по направлению).

Определим усилия, действующие на зубчатые колеса.

Рассмотрим равновесие вала АВ, предварительно при­ведя силы Р₁ и Р₂ к точкам, лежащим на оси вала.

Перенося силу Р₁ параллельно самой себе в точку L, надо добавить пару сил с моментом, равным моменту силы Р₁ относительно точки L, т. е.

Эта пара сил (момент) условно показана на рис. 2.71, в в виде дугообразной линии со стрелкой. Аналогично при переносе силы Р₂ в точку К надо присоединить (добавить) пару сил с моментом

Опоры вала, изображенного на рис. 2.71, а, надо рассматривать как пространственные шарнирные опоры, препятствующие линейным перемещениям в направлениях осей х и у (выбранная система координат показана на рис, 2.71, б).

Пользуясь расчетной схемой, изображенной на рис. 2.71, г, составим уравнения равновесия вала в вер­тикальной плоскости:

Составим проверочное уравнение:

следовательно, опорные реакции в вертикальной плоско­сти определены верно.

Рассмотрим равновесие вала в горизонтальной пло­скости:

Составим проверочное уравнение:

следовательно, опорные реакции в горизонтальной пло­скости определены верно.

Эпюры крутящих моментов М_z и изгибающих момен­тов М_х и М_у представлены на рис. 2.71, д.

Опасным является сечение К (см. рис. 2.71, г, д). Эквивалентный момент по гипотезе наибольших касатель­ных напряжений

Эквивалентное напряжение по гипотезе наибольших касательных напряжений для опасной точки вала

что значительно больше [n] = 4, следовательно, прочность вала обеспечена.

При расчете вала на прочность не учтено изменение напряжений во времени, поэтому и получился такой зна­чительный коэффициент запаса.

Пример 5. Определить размеры поперечного се­чения бруса (рис. 2.72, а). Материал бруса — сталь 30XГС с условными пределами текучести при растяжении и сжатии σ_о ,_2р = σ_тр = 850 Н/мм 2 , σ_0,2c = σ_Tc = 965 Н/мм 2 . Коэффициент запаса [n] = 1,6.

Брус работает на совместное действие рас­тяжения (сжатия) и кручения. При таком нагружении в поперечных сечениях возникают два внутренних силовых фактора: продольная сила и крутящий момент.

Эпюры продольных сил N и крутящих моментов M_z показаны на рис. 2.72, б, в. В данном случае определить положение опасного сечения по эпюрам N и M_z невоз­можно, так как размеры поперечных сечений участков бруса различны. Для выяснения положения опасного сечения следует построить эпюры нормальных и макси­мальных касательных напряжений по длине бруса.

вычисляем нормальные напряжения в поперечных сече­ниях бруса и строим эпюру о (рис. 2.72, г).

вычисляем максимальные касательные напряжения в по­перечных сечениях бруса и строим эпюру т_тах (рис* 2.72, д).

Вероятно, опасными являются точки контура попереч­ных сечений участков АВ и CD (см. рис. 2.72, а).

На рис. 2.72, e показаны эпюры σ и τ для попереч­ных сечений участка АВ.

Читайте также: Компрессор пк 5 25а у2 технические характеристики

Напомним, в данном случае (брус круглого попереч­ного сечения работает на совместное действие растяже­ния — сжатия и кручения) равноопасными являются все точки контура поперечного сечения.

На рис. 2.72, ж показаны напряжения на исходных площадках в опасной точке.

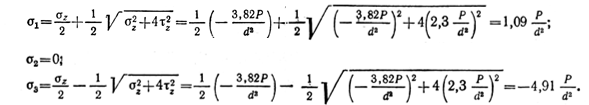Главные напряжения в опасной точке участка АВ:

По гипотезе прочности Мора эквивалентное напряже­ние для опасной точки этого участка

На рис. 2.72, з показаны эпюры а и т для попереч­ных сечений участка CD.

На рис. 2.72, и показаны напряжения на исходных площадках в опасной точке.

Главные напряжения в опасной точке участка CD:

По гипотезе прочности Мора эквивалентное напряже­ние для опасной точки рассматриваемого участка

Опасными оказались точки контура поперечных сече­ний участка АВ.

Условие прочности имеет вид:

Пример 2.76. Определить допускаемое значение силы Р из условия прочности стержня ВС (рис.2.73).Материал стержня — чугун с пределом проч­ности при растяжении σ_вр = 150 Н/мм 2 и пре­делом прочности при сжатии σ_вс = 450 Н/мм 2 . Требуемый коэффициент запаса [n] = 5.

Указание. Ломаный брус АBС расположен в го­ризонтальной плоскости, при­чем стержень AВ перпенди­кулярен к ВС. Силы Р, 2Р, 8Р лежат в вертикальной плоскости; силы 0,5 Р, 1,6 Р — в горизонтальной и перпендикулярны стержню ВС; силы 10Р, 16Р совпада­ ют с осью стержня ВС; пара сил с моментом m = 25Pd распо­ложена в вертикальной плоскости, перпендикулярной оси стерж­ня ВС.

Приведем силы Р и 0,5Р к центру тяжести поперечного сечения В.

Перенося силу Р параллельно самой себе в точку В, надо добавить пару сил с моментом, равным моменту силы Р относительно точки В, т. е. пару с моментом m₁ = 10 Pd.

Силу 0,5Р переносим вдоль ее линии действия в точку В.

Нагрузки, действующие на стержень ВС, показаны на рис. 2.74, а.

Строим эпюры внутренних силовых факторов для стержня ВС. При указанном нагружении стержня в его поперечных сечениях их возникает шесть: продольная сила N, поперечные силы Qx и Qy, крутящий момент Mz изгибающие моменты Мх и Му.

Эпюры N, Мz, Мх, Му представлены на рис. 2.74, б (ординаты эпюр выражены через Р и d).

Эпюры Qy и Qx не строим, так как касательные напряжения, соответствующие поперечным силам, имеют малую величину.

В рассматриваемом примере положение опасного сечения не очевидно, Предположительно, опасны сечения К (конец участка I) и С.

Определим величину и плоскость действия изгибающего момента Ми в сечении К, изображённом отдельно на рис. 2.74, в. На этом же рисунке показаны эпюры σ_И, σ_N, τ для сечения К.

Опасной является точка L. Напряжения на исходных площадках в точке L (рис. 2.74, г):

Главные напряжения в точке L:

По гипотезе прочности Мора эквивалентное напряжение для точки L

Определим величину и плоскость действия изгибающего момента Ми в сечении С, изображенном отдельно на рис. 2.74, д. На этом же рисунке показаны эпюры σ_И, σ_N, τ для сечения С.

Напряжения на исходных площадках в точке Н (рис. 2.74, е)

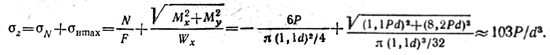Главные напряжения в точке Н:

По гипотезе прочности Мора эквивалентное напряже­ние для точки Н

Напряжения на исходных площадках в точке Е (рис. 2.74, ж):

Главные напряжения в точке Е:

По гипотезе прочности Мора эквивалентное напряже­ние для точки Е

Опасной оказалась точка L, для которой

Условие прочности имеет вид:

Контрольные вопросы и задания

1. Какое напряженное состояние возникает в поперечном сече­нии вала при совместном действии изгиба и кручения?

2. Напишите условие прочности для расчета вала.

3. Напишите формулы для расчета эквивалентного момента при расчете по гипотезе максимальных касательных напряжений и гипо­тезе энергии формоизменения.

4. Как выбирается опасное сечение при расчете вала?

• Свежие записи
  • Чем отличается двухтактный мотор от четырехтактного
  • Сколько масла заливать в редуктор мотоблока
  • Какие моторы бывают у стиральных машин
  • Какие валы отсутствуют в двухвальной кпп
  • Как снять стопорную шайбу с вала
  • Правообладателям
  • Политика конфиденциальности

  Механика © 2023
  Информация, опубликованная на сайте, носит исключительно ознакомительный характер

  
  

  источники:

  https://evakuatorinfo.ru/uslovie-prochnosti-vala-diametrom-d-po-kasatelnym-napryazheniyam

  📸 Видео

  9.1 Расчет валов приводаСкачать

  

  Подбор круглого, прямоугольного и квадратного сечения. Сопромат.Скачать

  

  Сопромат. Часть 1. Растяжение (сжатие). Построение эпюр продольных сил и нормальных напряжений.Скачать

  

  Основы Сопромата. Расчеты на прочность. Общая идеяСкачать

  

  Сопромат. Практическое занятие №1.4Скачать

  

  9.4. Расчет валов и осейСкачать

  

  Основы Сопромата. Подбор сечения конструктивного элементаСкачать

  

  Определение реакций опор в балке. Сопромат.Скачать

  

  СОПРОМАТ. Эпюры нормальных и касательных напряжений. IV теория прочности. Задача 3.2. Часть 2.Скачать

  

  Изгиб. Нормальные, касательные, главные напряжения. Расчёт на прочность. Балка из двутавра. (Начало)Скачать

  

  Изгиб балок. Нормальные, касательные напряжения. Формула Журавского. Сопромат - Тайные Знания 5.Скачать

  

  Изгиб с кручениемСкачать

  

  10. Подбор сечения при растяжении сжатии ( практический курс по сопромату )Скачать

  

  Вал. Расчет на прочность при косом изгибе и крученииСкачать