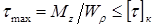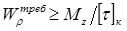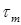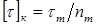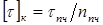Условие прочности при кручении: прочность вала считается обеспеченной, если наибольшие касательные напряжения, возникающие в его опасном поперечном сечении, не превышают допускаемых напряжений на кручение :
Формула служит для проверочного расчета вала на прочность.
Допускается незначительное (до 5 %) превышение расчетного напряжения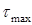 
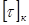
над допускаемым напряжением 
.
При проектировочном расчете требуемый полярный момент сопротивления определяется по формуле условия прочности при кручении :
.
Для вала постоянного диаметра опасным сечением при кручении является сечение, в котором возникает наибольший крутящий момент. Если сечение вала не постоянно по длине, может оказаться, что наибольшие касательные напряжения возникают не там, где крутящий момент максимален. Следовательно, в этом случае вопрос об опасном сечении должен быть исследован дополнительно.
Допускаемое напряжение :
для пластичных материалов назначается в зависимости от предела текучести () при кручении (сдвиге):
.
для хрупких материалов назначается в зависимости от предела прочности:
.
- Техническая механика
- Сопротивление материалов
- Применение теорий прочности для расчетов
- Изгиб и кручение
- Кручение и растяжение или сжатие
- ПроСопромат.ру
- Технический портал, посвященный Сопромату и истории его создания
- Изгиб с кручением
- Сложное сопротивление.
- Косой изгиб.
- Изгиб с растяжением (сжатием).
- Внецентренное растяжение или сжатие.
- Кручение с изгибом.
- 💡 Видео
Видео:Изгиб с кручениемСкачать
Техническая механика
Сопротивление материалов
Видео:КРУЧЕНИЕ ВАЛА. Касательные напряжения. Сопромат.Скачать
Применение теорий прочности для расчетов
Изгиб и кручение
Сочетание деформаций изгиба и кручения испытывает большинство валов, которые обычно представляют собой прямые брусья круглого или кольцевого сечения.
При расчете валов мы будем учитывать только крутящий или изгибающий моменты, действующие в опасном поперечном сечении, и не будем принимать во внимание поперечные силы, так как соответствующие им касательные напряжения относительно невелики.
Максимальные нормальные и касательные напряжения у круглых валов вычисляют по формулам:
причем для круглых валов Wр = 2W .
При сочетании изгиба и кручения опасными будут точки опасного поперечного сечения вала, наиболее удаленные от нейтральной оси.
Применив третью теорию прочности, получим:
Выражение, стоящее в числителе, называют эквивалентным моментом:
Тогда расчетная формула для круглых валов примет вид:
(валы обычно изготовляют из материала, у которого [σр] = [σс] = [σ] ).
По этой формуле расчет круглых валов ведут, как на изгиб, но не по изгибающему, а по эквивалентному моменту. Применив энергетическую теорию прочности, получим:
т. е. по энергетической теории прочности:
Для расчетов деталей на сочетание деформаций поперечного изгиба и кручения необходимо, как правило, составить расчетную схему конструкции и построить эпюры изгибающих и крутящих моментов, определить предположительно опасные сечения, после чего, применив одну из теорий прочности, произвести необходимые расчеты.
Читайте также: Диаметр рулевого вала поло седан
На рисунке ниже представлен пример расчета трансмиссионного вала, подверженного деформациям изгиба и кручения, на прочность. На основе чертежа вала в аксонометрической проекции составлена его расчетная схема и построены эпюры изгибающих и крутящих моментов.
Расчет производят в следующей последовательности:
- По эпюрам моментов определяют наиболее опасные сечения вала;
- Подсчитывают значения моментов в этих сечениях и, применяя одну из теорий прочности, рассчитывают эквивалентные напряжения;
- В соответствии с условием прочности, оценивают работоспособность вала при данных нагрузках.
Кручение и растяжение или сжатие
Сочетание деформаций кручения и растяжения испытывают, например, болты и крепежные винты, а сочетание деформаций кручения и сжатия — винты домкратов и винтовых прессов, сверла и шпиндели сверлильных станков. Эти детали обычно изготовляют из материалов, у которых [σр] = [σс] = [σ] .
Нормальные и максимальные касательные напряжения в этих случаях определяют по формулам:
Применив третью теорию прочности, получим расчетную формулу:
Применив энергетическую теорию прочности, получим:
Видео:Расчет вала на прочность и жесткость. Эпюра крутящих моментовСкачать
ПроСопромат.ру
Видео:Кручение. Часть 5 Условие прочностиСкачать
Технический портал, посвященный Сопромату и истории его создания
Видео:Изгиб с кручением пример решения задач по сопротивлению материалов. Теории прочностиСкачать
Изгиб с кручением
Такие части машин, как валы редко работают на чистое скручивание. Прямой вал при работе изгибается под действием собственного веса, веса шкивов, натяжений ремней и усилий, возникающих в различных зацеплениях различных передач. Таким образом, большинство скручиваемых элементов машин работают на совместное действие изгиба и кручения. К числу подобных элементов относятся и коленчатые валы.
При расчете элементов, работающих на изгиб и кручение необходимо знать расчетные значения изгибающих моментов Ми и крутящего момента Т, где Q – вес шкивов, t – натяжение ремней, Р – окружная сила.
Затем строятся эпюры изгибающих моментов от сил, лежащих в горизонтальной Мг и вертикальной Мв плоскостях и суммарный изгибающий момент Мс по формуле:
Схема действующих моментов:
Определяется расчетный (эквивалентный) момент по одной из теорий прочности.
Напряженное состояние в условиях изгиба с кручением
Читайте также: Компрессор безмасляный of302 25b jun air инструкция
При расчетах валов, изготовленных из конструкционных сталей, используются третья и четвертая теории прочности, согласно которым расчетные (эквивалентные) напряжения 
определяются так: 
(1)
где напряжения рассчитывают по известным формулам:
где W – момент сопротивления при изгибе, W=0,1d 3 ;
2W=Wp – момент сопротивления при кручении, WP=0,2d 3 =2W.
Подставим эти значения в (1), получим:
Расчетный момент по третьей и четвертой теории прочности:
Условие прочности:
В случае если на вал действует осевая сила N, условие прочности имеет вид:
где А – площадь кругового вала, А=0,785d 2 .
Напряженное состояние в условиях изгиба и кручения:
Видео:Изгиб с кручением. Расчет на прочностьСкачать
Сложное сопротивление.
Сложное сопротивление – одновременное действие на брус нескольких простых видов деформаций: растяжения-сжатия, сдвига, кручения и изгиба. Например, совместное действие растяжения и кручения.
Видео:Вал. Расчет на прочность при косом изгибе и крученииСкачать
Косой изгиб.
Косой изгиб – это изгиб, при котором плоскость действия изгибающего момента не совпадает ни с одной из главных плоскостей инерции сечения бруса.
В общем случае при косом изгибе в поперечных сечениях возникают четыре внутренних силовых фактора: поперечные силы Qx, Qy и изгибающие моменты Mx , My. Таким образом, косой изгиб можно рассматривать как сочетание двух плоских поперечных изгибов во взаимно перпендикулярных плоскостях. Влиянием поперечных сил на прочность и жесткость бруса обычно пренебрегают.
Нейтральная линия при косом изгибе всегда проходит через центр тяжести сечения.
Условие прочности при косом изгибе:
где ymax, xmax — координаты точки сечения, наиболее удаленной от нейтральной оси.
Для сечений, имеющих две оси симметрии, максимальные напряжения будут в угловых точках, а условие прочности:
где Wx , Wy – осевые моменты сопротивления сечения относительно соответствующих осей.
Если материал бруса не одинаково работает на растяжение и на сжатие, то проверку его прочности выполняют по допускаемым и растягивающим и сжимающим напряжениям.
Прогибы при косом изгибе определяют, используя принцип независимости действия сил, геометрическим суммированием прогибов вдоль направления главных осей:
Видео:Расчет вала на изгиб с кручениемСкачать
Изгиб с растяжением (сжатием).
При таком виде сложного сопротивления внутренние силовые факторы приводятся к одновременному действию продольной силы N и изгибающего момента M.
Рассмотрим случай центрального растяжения бруса в сочетании с косым изгибом. На консольный брус действует сила F, составляющая некоторый угол с продольной осью бруса и не лежащая ни в одной из главных плоскостей сечения. Сила приложена в центре тяжести торцевого сечения бруса:
Читайте также: Датчик скорости выходного вала опель астра h
К расчёту на прочность бруса при изгибе с растяжением:
a — нагружение бруса; б — внутренние силовые факторы в поперечном сечении;
Разложим силу F на три составляющие. Тогда внутренние силовые факторы приобретут следующий вид:
Напряжение в произвольно выбранной точке Д, имеющей координаты (хд, уд), пренебрегая действием поперечных сил, будут определяться по формуле:
где А — площадь поперечного сечения.
Если сечение имеет две оси симметрии (двутавр, прямоугольник, круг), наибольшее напряжение определяют по формуле:
Условие прочночти имеет вид:
Также как и в случае косого изгиба, если материал бруса не одинаково работает на растяжение и на сжатие, то проверку прочности проводят по допускаемым растягивающим и сжимающим напряжениям.
Видео:Сопромат. Практическое занятие №1.4Скачать
Внецентренное растяжение или сжатие.
При таком виде сложного сопротивления продольная сила приложена не в центре тяжести поперечного сечения бруса.
К расчёту на прочность бруса при внецентренном растяжении
a — нагружение бруса; б — внутренние силовые факторы в поперечном сечении;
Приведём силу F к центру тяжести:
где уF , xF — координаты точки приложения силы F.
В произвольной точке Д, с координатами (хд, уд), нормальное напряжение определяется по фомуле:
Условие прочности для бруса, изготовленного из материала, одинаково сопротивляющегося растяжению и сжатию, имеет вид:
Для бруса, который неодинаково работает на растяжение и на сжатие проверка прочности по допускаемым растягивающим и сжимающим напряжениям.
Видео:ПОДБОР ДВУТАВРА И ШВЕЛЛЕРА. Проверка прочности балки. Сопромат.Скачать
Кручение с изгибом.
Сочетание деформаций изгиба и кручения характерно для работы валов машин.
Напряжения в сечениях вала возникают от кручения и от изгиба. При изгибе появляются нормальные и касательные напряжения:
Эпюры напряжений в сечении бруса при кручении с изгибом
Нормальное напряжение достигает максимума на поверхности:
Касательное напряжение от крутящего момента Mz достигает максимума также на поверхности вала:
Из третьей и четвёртой теории прочности:
При кручении с изгибом условие прочности имеет вид:
- Свежие записи
- Чем отличается двухтактный мотор от четырехтактного
- Сколько масла заливать в редуктор мотоблока
- Какие моторы бывают у стиральных машин
- Какие валы отсутствуют в двухвальной кпп
- Как снять стопорную шайбу с вала
- Правообладателям
- Политика конфиденциальности
Механика © 2023
Информация, опубликованная на сайте, носит исключительно ознакомительный характер💡 Видео
Кручение. Часть 6 Жесткость валаСкачать
Изгиб с кручением пример решения задач по сопротивлению материаловСкачать
23. Кручение с изгибом ( практический курс по сопромату )Скачать
5. Изгиб с кручениемСкачать
Кручение с изгибом (часть 1)Скачать
Определение реакций опор в балке. Сопромат.Скачать
КОСОЙ ИЗГИБ. БАЛКА. Сопромат.Скачать
Изгиб с кручениемСкачать
