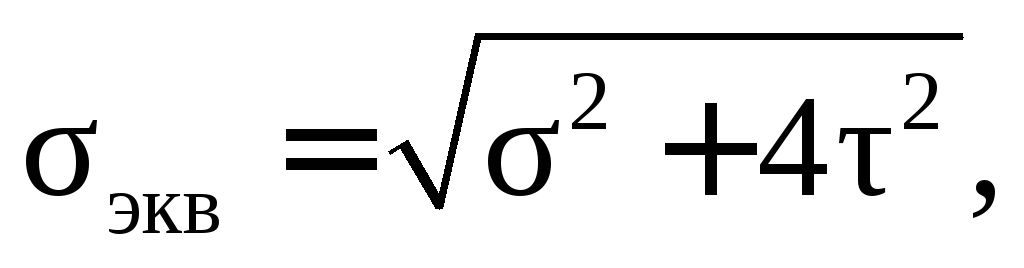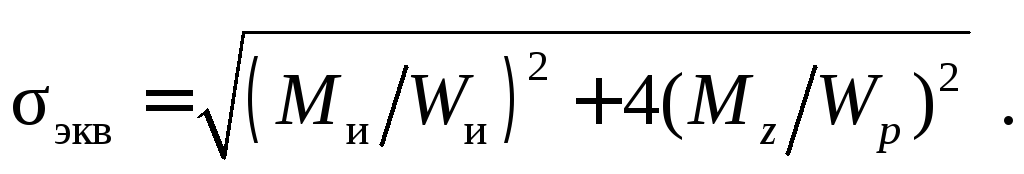При ориентировочном расчете валов влияние изгиба не учитывалось, но допускаемые напряжения на кручение принимались весьма невысокими, что должно было в известной мере компенсировать ошибку, являющуюся следствием пренебрежения изгибом.
Применение гипотез прочности позволяет рассчитывать валы, учитывая совместное действие изгиба и кручения.
При расчете валов, а также других элементов конструкций, испытывающих одновременное действие изгиба и кручения, влиянием поперечных сил, как правило, пренебрегают, так как соответствующие им касательные напряжения в опасных точках бруса, невелики по сравнению с касательными напряжениями от кручения и нормальными напряжениями от изгиба.
На рис. 19.16, а показан вал, на который насажены зубчатое колесо диаметром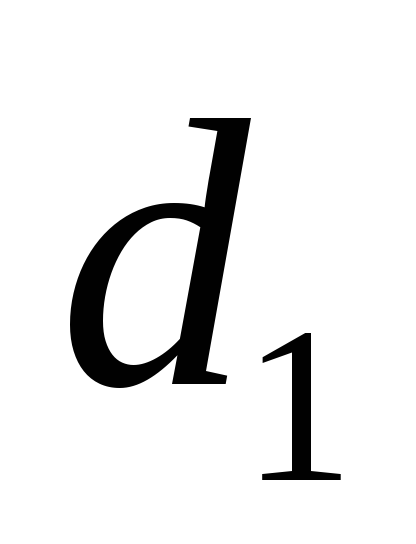 
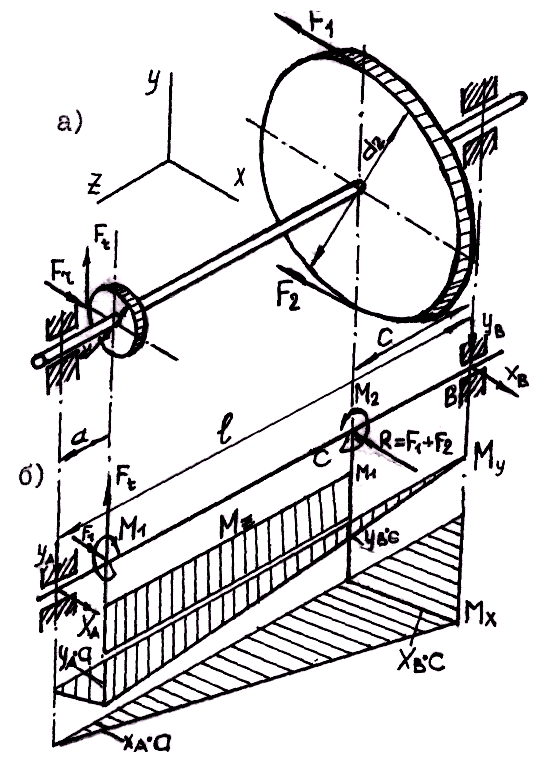
и шкив ременной передачи диаметром 
. На зубчатое колесо действуют окружная 
и радиальная 
силы, на шкив – силы 
и 
натяжения ветвей ремня. Для составления расчетной схемы вала (рис. 19.16, б) все силы должны быть приведены к его оси. При переносе силы 
к оси вала добавляется скручивающая пара с моментом 
(рис. 19.17, а); аналогично при приведении сил 
и 
получается скручивающая пара с моментом 
(рис. 19.17, б).
Рис. 19.16. Изгиб с кручением вала
Рис. 19.17. Перенос сил к оси вала
При равномерном вращении вала (только такой случай и рассматривается) , что следует из основного уравнения динамики для вращательного движения.
На основе расчетной схемы определяют опорные реакции и строят эпюры , по которым определяют опасное сечение вала.
Для вала, диаметр которого по всей длине постоянен, опасным будет сечение, в котором одновременно возникают наибольшие крутящий 
и изгибающий 
моменты. В рассматриваемом случае опасным будет сечение C под серединой шкива.
Валы, как правило, изготовляют из среднеуглеродистой конструкционной или реже – легированной стали. Их расчет выполняют на основе третьей или пятой гипотез прочности.
Составим расчетную зависимость по третьей гипотезе прочности.
подставляя в нее значения 
и 
, получаем
Учитывая, что для круглого (сплошного или кольцевого) сечения , имеем
Внешне эта формула аналогична расчетной зависимости для определения максимальных нормальных напряжений при изгибе, поэтому величину, стоящую в числителе, называют эквивалентным (или приведенным) моментом, при этом условие прочности имеет вид
Расчет бруса круглого поперечного сечения на изгиб с кручением ведется аналогично расчету на изгиб, но вместо изгибающего момента в расчетную формулу входит так называемый эквивалентный момент, который зависит от изгибающих и крутящего моментов, а также от принятой гипотезы прочности. По гипотезе наибольших касательных напряжений,
При проектном расчете определяют требуемое значение момента сопротивления поперечного сечения:
Читайте также: Мотоблок без вала отбора мощности
Учитывая, что для сплошного круглого сечения ,получаем следующую формулу для определения требуемого диаметра вала:
Понятие «эквивалентный момент» не имеет смысла при изгибе с кручением бруса некруглого поперечного сечения. Неприменимо оно и в случае, если помимо изгиба и кручения брус круглого сечения испытывает растяжение или сжатие.
Для бруса с постоянным диаметром опасная точка находится в сечении, для которого эквивалентный момент имеет наибольшее значение. Это сечение также называют опасным. Для отыскания опасного сечения иногда помимо эпюр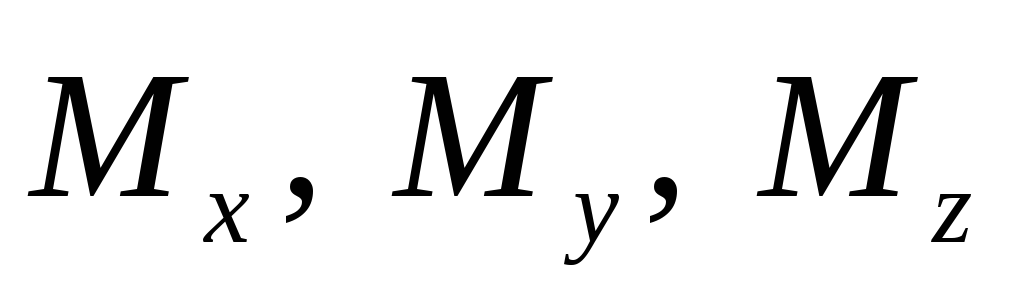 
строят эпюру 
, а затем эпюру 
. Практически в этом нет необходимости; в случае, если по эпюрам 
положение опасного сечения определить нельзя, проще вычислить 
для нескольких сечений, чем строить эпюры 
и 
.
- Условие прочности вала при совместном действии крутящего и изгибающего моментов
- Условие прочности вала при совместном действии крутящего и изгибающего моментов ( реферат , курсовая , диплом , контрольная )
- 4. Условие прочности вала при совместном действии крутящего и изгибающего моментов. Определение диаметра вала по теории наибольших касательных напряжений, по энергетической теории.
- 5. Расчет на жесткость при кручении вала, определение его диаметра из условия жесткости при кручении.
- 6. Геометрические характеристики сечений. Статический момент, момент инерции, момент сопротивления простых сечений.
- 💡 Видео
Видео:Расчет вала на прочность и жесткость. Эпюра крутящих моментовСкачать
Условие прочности вала при совместном действии крутящего и изгибающего моментов
По гипотезе наибольших касательных напряжений, M экв M 2 M 2M 2 M 2 M 2. и Z x y z При проектном расчете определяют требуемое значение момента сопротивления поперечного сечения: Wи Mэкв у. Учитывая, что для сплошного круглого сечения W рd 3 0,1d 3, 32 получаем следующую формулу для определения требуемого диаметра вала: d 3 32M экв 3 M экв. р у 0,1 у Понятие «эквивалентный момент» не имеет смысла… Читать ещё >
Видео:ПОДБОР ДВУТАВРА И ШВЕЛЛЕРА. Проверка прочности балки. Сопромат.Скачать
Условие прочности вала при совместном действии крутящего и изгибающего моментов ( реферат , курсовая , диплом , контрольная )
При ориентировочном расчете валов влияние изгиба не учитывалось, но допускаемые напряжения на кручение принимались весьма невысокими, что должно было в известной мере компенсировать ошибку, являющуюся следствием пренебрежения изгибом.
Применение гипотез прочности позволяет рассчитывать валы, учитывая совместное действие изгиба и кручения.
При расчете валов, а также других элементов конструкций, испытывающих одновременное действие изгиба и кручения, влиянием поперечных сил, как правило, пренебрегают, так как соответствующие им касательные напряжения в опасных точках бруса, невелики по сравнению с касательными напряжениями от кручения и нормальными напряжениями от изгиба.
На 19.16, а показан вал, на который насажены зубчатое колесо диаметром d1 и шкив ременной передачи диаметром d2. На зубчатое колесо действуют окружная Ft и радиальная Fr силы, на шкив — силы F1 и F2 натяжения ветвей ремня. Для составления расчетной схемы вала (19.16, б) все силы должны быть приведены к его оси. При переносе силы Ft к оси вала добавляется скручивающая пара с моментом M 1 Ft (d1 2) (19.17, а); аналогично при приведении сил F1 и F2 получается скручивающая пара с моментом M F (d 2) F (d 2) (F F)(d2 2) (19.17, б). 2 1 2 2 2 1 2 Изгиб с кручением вала Перенос сил к оси вала При равномерном вращении вала (только такой случай и рассматривается) M 1 M2, что следует из основного уравнения динамики для вращательного движения.
Читайте также: Ауди 80 б3 замена подшипника первичного вала
На основе расчетной схемы определяют опорные реакции и строят эпюры M z, M x и M y, по которым определяют опасное сечение вала. M и M 2 M 2. x y Для вала, диаметр которого по всей длине постоянен, опасным будет сечение, в котором одновременно возникают наибольшие крутящий M z и изгибающий M и моменты. В рассматриваемом случае опасным будет сечение C под серединой шкива [12, «https://referat.bookap.info»].
Валы, как правило, изготовляют из среднеуглеродистой конструкционной или реже — легированной стали. Их расчет выполняют на основе третьей или пятой гипотез прочности.
Составим расчетную зависимость по третьей гипотезе прочности. По формуле уэкв у2 4ф2, подставляя в нее значения у и ф, получаем у экв M W 2 4(M z W)2. ии p Учитывая, что для круглого (сплошного или кольцевого) сечения W p 2Wи, имеем W 2 W)2 M 2 M 2 у M (M И Z. экв ии zи Wи.
Внешне эта формула аналогична расчетной зависимости для определения максимальных нормальных напряжений при изгибе, поэтому величину, стоящую в числителе, называют эквивалентным (или приведенным) моментом, при этом условие прочности имеет вид уэкв M экв у. Wи Расчет бруса круглого поперечного сечения на изгиб с кручением ведется аналогично расчету на изгиб, но вместо изгибающего момента в расчетную формулу входит так называемый эквивалентный момент, который зависит от изгибающих и крутящего моментов, а также от принятой гипотезы прочности.
По гипотезе наибольших касательных напряжений, M экв M 2 M 2M 2 M 2 M 2. и Z x y z При проектном расчете определяют требуемое значение момента сопротивления поперечного сечения: Wи Mэкв у. Учитывая, что для сплошного круглого сечения W рd 3 0,1d 3, 32 получаем следующую формулу для определения требуемого диаметра вала: d 3 32M экв 3 M экв. р у 0,1 у Понятие «эквивалентный момент» не имеет смысла при изгибе с кручением бруса некруглого поперечного сечения. Неприменимо оно и в случае, если помимо изгиба и кручения брус круглого сечения испытывает растяжение или сжатие.
Для бруса с постоянным диаметром опасная точка находится в сечении, для которого эквивалентный момент имеет наибольшее значение. Это сечение также называют опасным. Для отыскания опасного сечения иногда помимо эпюр M x, M y, M z строят эпюру M и, а затем эпюру M экв. Практически в этом нет необходимости; в случае, если по эпюрам M x, M y, M z положение опасного сечения определить нельзя, проще вычислить M экв для нескольких сечений, чем строить эпюры M и и M экв .
Видео:КРУЧЕНИЕ ВАЛА. Касательные напряжения. Сопромат.Скачать
4. Условие прочности вала при совместном действии крутящего и изгибающего моментов. Определение диаметра вала по теории наибольших касательных напряжений, по энергетической теории.
На изгиб с кручением работают все валы. Вал находится в сложном напряжённом состоянии от внешних нагрузок Мизг и Ткр
Читайте также: Схема москвы с камер коллежским валом
По теории наибольших касательных напряжений можно определить эквивалентное напряжение:
По энергетической теории прочности:
σэкв= ≤ [σэкв] , где Мэкв=√(М 2 +Т 2 ) – по теории наибольших касательных напряжений
Мэкв=√(М 2 +0.75Т 2 ) – по энергетической теории
Внешний изгибающий момент действует на вал в 2 плоскостях: в вертикальной и горизонтальной.
Диаметр вала по теории наибольших касательных напряжений:
Т.к. Wx= d 3 ≈0.1d 3 , то dвала ≥ или dвала ≥
Видео:Изгиб с кручениемСкачать
5. Расчет на жесткость при кручении вала, определение его диаметра из условия жесткости при кручении.
Расчет вала на жесткость. Во многих случаях вал должен удовлетворять не только условию прочности, но и жесткости.
За меру жесткости при кручении принимают относительный угол закручивания вала. Условие жесткости бруса при кручении состоит в том, чтобы максимальный относительный угол закручивания не превышал некоторого заданного допускаемого
G—коэффициент Гука, —полярный момент инерции
Допускаемый угол закручивания зависит от назначения вала и принимается в пределах 0,25. 1,0 град/м.
Определение предельной нагрузки , должен быть известен материал и нагрузка.
Определение геометрических параметров:
Видео:Прочность и жесткость валов. Часть 9. Расчет на жесткость промежуточного вала (КЦ-редуктор)Скачать
6. Геометрические характеристики сечений. Статический момент, момент инерции, момент сопротивления простых сечений.
Статические моменты плоских сечений. Сопротивление элементов различным видам деформаций зависит не только от площади, но и от формы сечения и его ориентации к направлению нагрузок. Если для исследования растяжения (сжатия) элемента достаточно знать площадь его сечения, то при исследовании изгиба и кручения необходимо иметь сведения о геометрических характеристиках сечения, существенно зависящих от его формы. К ним относятся статические моменты, моменты инерции и моменты сопротивления сечения.
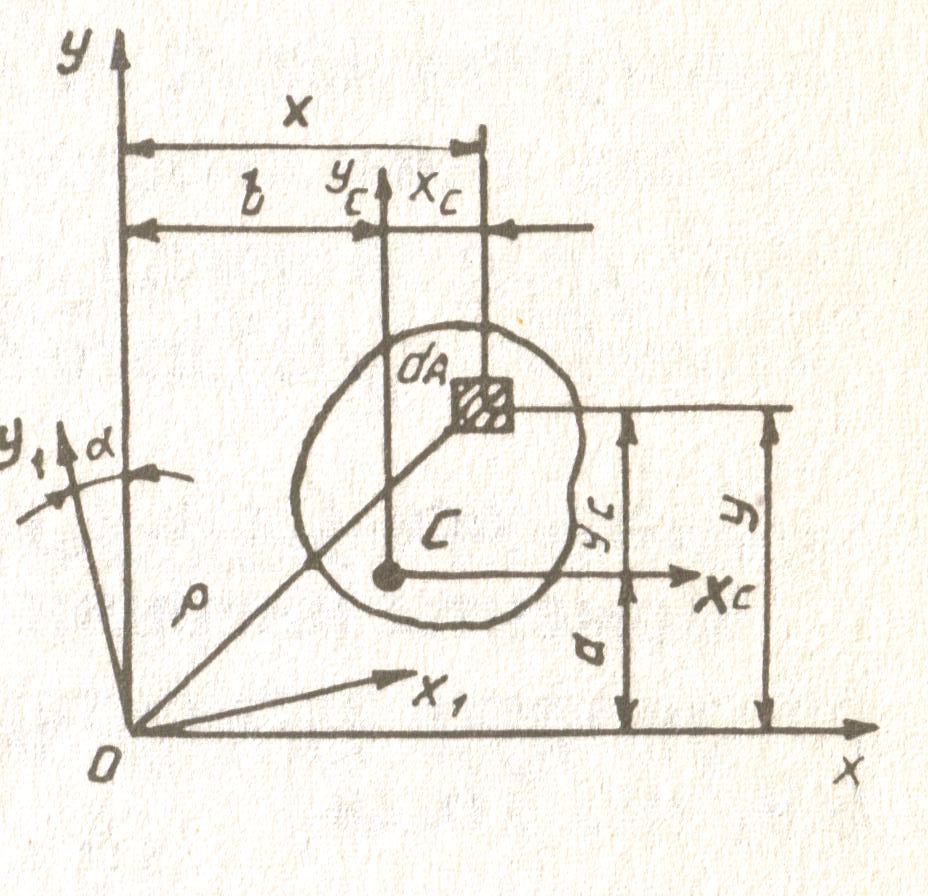
С татическим моментом сечения относительно оси называют взятую по всей площади сумму произведений площадей элементарных площадок dA на расстоянии от них до этой оси: ;
При известных статических моментах и площади сечения А координаты его центра тяжести можно определить по формулам: ;
Осевые моменты инерции. Осевыми моментами инерции плоского сечения относительно оси называется взятая по всей площади сечения сумма произведений площадей элементарных площадок на квадраты расстояний от них до этой оси: Полярный момент инерции сечения: , где ρ – расстояние от площадки dA до точки (полюса), относительно которой вычисляется полярный момент инерции. Очевидно, что: . Центробежный момент инерции сечения относительно двух взаимно перпендикулярных осей:
Моменты сопротивления сечений.
[мм 3 , м 3 ] – осевой момент сопротивления сечения относительно оси
[мм 3 , м 3 ] – полярный момент сопротивления сечения
- Свежие записи
- Чем отличается двухтактный мотор от четырехтактного
- Сколько масла заливать в редуктор мотоблока
- Какие моторы бывают у стиральных машин
- Какие валы отсутствуют в двухвальной кпп
- Как снять стопорную шайбу с вала
💡 Видео
Вал. Расчет на прочность при косом изгибе и крученииСкачать
Сопромат №4: Расчет вала на прочность и жесткостьСкачать
Расчет вала на изгиб с кручениемСкачать
Сопротивление материалов. Лекция: расчёт на прочность при растяжении и сжатииСкачать
Прочность и жесткость валов. (Зубчатый редуктор). Часть 3: Расчетные схемы валов.Скачать
Прочность и жесткость валов. Часть 6: Эпюры моментов выходного вала (цилиндрическая передача).Скачать
Прочность и жесткость валов. (Зубчатый редуктор). Часть 1: Введение.Скачать
Основы Сопромата. Подбор сечения конструктивного элементаСкачать
Solidworks расчет на прочностьСкачать
7. Подбор сечения при изгибе ( практический курс по сопромату )Скачать
9.1 Расчет валов приводаСкачать
Прочность и жесткость валов. Часть 8. Расчет на прочность промежуточного вала (КЦ-редуктор).Скачать
Основы Сопромата. Расчеты на прочность. Общая идеяСкачать
БАЛКА - 90 СТУДЕНТОВ САМОСТОЯТЕЛЬНО СТРОЯТ ЭПЮРЫ после просмотра этого видео!Скачать
Видеоурок 6. Расчеты на прочность и жесткость при изгибе.Скачать
