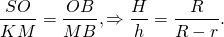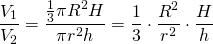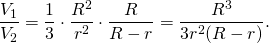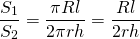В данный конус вписать цилиндр (2 видео)

Найдите радиус основания цилиндра наибольшего объёма, вписанного в конус, радиус основания которого равен 3.

Содержание

Ответ
Узнать ещё
Цилиндр вписан в конус
Тригонометрия
Ещё по теме
Геометрия. 11 класс
📽️ Видео

Ответ

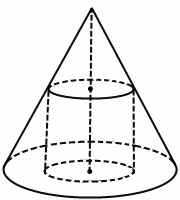
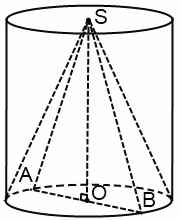
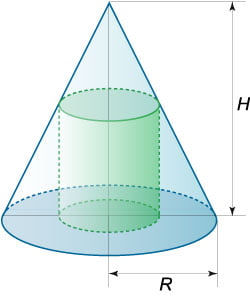
2. Обозначим через h и r высоту и радиус основания цилиндра, вписанного в конус с вершиной A (рис.1). Рассмотрим осевое сечение конуса – равнобедренный треугольник ABC с высотой AO = H и основанием BC = 2· 3 = 6 (рис.2). Плоскость ABC пересекает цилиндр, вписанный в конус, по его осевому сечению – прямоугольнику KLMN , где точки K и L лежат соответственно на отрезках AB и AC , а точки M и N – на отрезке BC , причём KL = 2r , KN = LM = h . Пусть P – точка пересечения AO и KL . Треугольник APL подобен треугольнику AOC , поэтому
= , или = ,
откуда h = H(1 — ) . Пусть V(r) – объём цилиндра, где 0 V(r) = π r 2 h = π Hr 2 (1 — ) = π H(r 2 — ).
Найдём наибольшее значение функции V(r) на промежутке (0;3) .
V’(r) = π H(2r — r 2 ) = π Hr(2 — r).
Промежутку (0;3) принадлежит единственный корень ( r = 2 ) полученного уравнения. Если 0 0 . Поэтому на промежутке (0;2) функция V(r) возрастает. Если 2

Пишите нам

Проект осуществляется при поддержке и .

Видео:Конус. 11 класс.Скачать

Узнать ещё

Знание — сила. Познавательная информация

Видео:Врезка | Цилиндр и конус | Автор Прохоренко КонстантинСкачать

Цилиндр вписан в конус

Цилиндр вписан в конус, если одно основание цилиндра лежит в плоскости основания конуса, а окружность другого основания — на боковой поверхности конуса. Конус, соответственно, в этом случае называется описанным около цилиндра.

Оси конуса и вписанного в него цилиндра совпадают. Верхнее основание цилиндра совпадает с сечением конуса плоскостью, параллельной основанию.

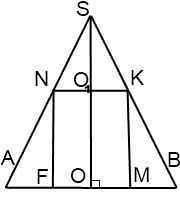
Рассмотрим осевое сечение комбинации тел. Оно представляет собой равнобедренный треугольник с вписанным в него прямоугольником.

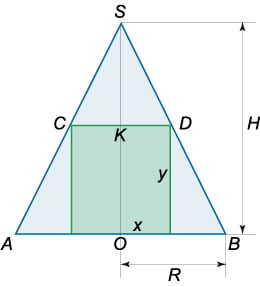
Здесь SO=H — высота конуса, OA=OB=R — радиус конуса, OF=OM=r — радиус цилиндра, OO1=h — высота цилиндра, SA=SB=l — образующие конуса, NF=KM=h — образующие цилиндра.

Прямоугольные треугольники SOB и KMB подобны (по общему острому углу B). Из подобия треугольников следует пропорциональность соответствующих сторон:

Найдем отношение объемов конуса и вписанного в него цилиндра:

С учетом предыдущего соотношения для высот конуса и цилиндра, имеем:

Найдем отношение боковой поверхности конуса к боковой поверхности вписанного цилиндра:

Читайте также: Чем можно раскоксовать кольца в цилиндре

Из прямоугольного треугольника SOB по теореме Пифагора

Видео:Цилиндр, конус, шар, 6 классСкачать

Тригонометрия

Ещё по теме

Окно имеет форму прямоугольника, ограниченного сверху полукругом (рисунок \(3\)). Периметр окна равен \(P.\) Определить радиус полукруга \(R,\) при котором площадь окна является наибольшей.

Найдите \( \sin \alpha \) и \( tg \alpha \) , если \( \cos \alpha=-\dfrac12 \) и \( \dfrac ;

Площадь ромба равна \( 10.8 \) см 2 , а площадь круга, вписанного в этот ромб — \( 2.25\pi \) см 2 .

1. Определите длину радиуса круга, вписанного в ромб (в см).

2. Вычислить длину стороны ромба (в см).

Диагональ равнобокой трапеции является биссектрисой ее острого угла и делит среднюю линию трапеции на отрезки длиной 15 см и 33 см. Вычислить (в см 2 ) площадь трапеции.

Дан ромб, диагонали которого равны \(d1=4\) см, \(d2=6\) см. Острый угол равен \(α = 30°\) . Найдите площадь фигуры через сторону и угол.

Найти координаты точки на единичной окружности, полученной поворотом точки \( A\left( 1;0 \right) \) на \( -225<>^\circ \) .

Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!

О сайте

На нашем сайте вы найдете множество полезных калькуляторов, конвертеров, таблиц, а также справочных материалов по основным дисциплинам.

Самый простой способ сделать расчеты в сети — это использовать подходящие онлайн инструменты. Воспользуйтесь поиском, чтобы найти подходящий инструмент на нашем сайте.

calcsbox.com

На сайте используется технология LaTeX.
Поэтому для корректного отображения формул и выражений
пожалуйста дождитесь полной загрузки страницы.

Копирование материалов запрещено

Видео:Линия пересечения двух поверхностей конус и цилиндр (Метод секущих плоскостей)Скачать

Геометрия. 11 класс

Конспект урока

Урок №10. Комбинации тел вращения

Перечень вопросов, рассматриваемых в теме:

комбинации конуса и цилиндра, конуса и усеченного конуса, цилиндра и усеченного конуса, нескольких сфер;
цилиндр, описанный около конуса, конус, описанный около цилиндра, усеченный конус, описанный около конуса и цилиндра;
цилиндр, вписанный в конус, конус, вписанный в цилиндр, усеченный конус, вписанный в конус и цилиндр.

Читайте также: Вертикальный цилиндр закрыт горизонтально

Конус вписан в цилиндр, если основание конуса совпадает с основанием цилиндра, а вершина совпадает с центром другого основания цилиндра. Цилиндр, соответственно, в этом случае называется описанным около конуса.

Конус вписан в другой конус, если его вершина лежит в центре основания второго конуса, а основание лежит на боковой поверхности.

Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. и др. Геометрия. 10–11 классы : учеб. для общеобразоват. организаций : базовый и углубл. уровни – М. : Просвещение, 2014. – 255, сс. 136-147.

Шарыгин И.Ф., Геометрия. 10–11 кл. : учеб. для общеобразоват. учреждений – М.: Дрофа, 2009. – 235, : ил., ISBN 978–5–358–05346–5, сс. 77-84.

Открытые электронные ресурсы:

Теоретический материал для самостоятельного изучения

1. Комбинации цилиндра и конуса

В любой конус можно вписать цилиндр.

Осевое сечение цилиндра, вписанного в конус — представляет собой равнобедренный треугольник с вписанным в него прямоугольником.

NF=KM=h (l)— образующие цилиндра.

∆SOB∆KMB (по общему острому углу B)

, то есть: .

Отношение боковой поверхности конуса к боковой поверхности вписанного цилиндра (через радиусы основания и образующие)

, то есть .

В любой цилиндр можно вписать конус.

OS — ось цилиндра и ось конуса, высота цилиндра и конуса

OA — радиус конуса и радиус цилиндра

CA=DB=l — образующие цилиндра

∆SOA, ∆SCA, ∆SDB и ∆SOB — прямоугольные

∆SOA=∆SCA, ∆SDB = ∆SOB, поэтому 2S_∆ASB=2S_ACDB.

Отношение боковой поверхности конуса к боковой поверхности описанного около него цилиндра (через радиус основания и высоту)

, то есть .

2. Комбинация двух конусов

Читайте также: Если в цилиндре масло что это значит

OS — ось конусов, высота большого конуса

OA — радиус большого конуса

В дне кашпо, имеющего форму конуса с площадью боковой поверхности 15π дм и радиусом основания 3 дм, сделано отверстие для того чтобы в него можно было вставить горшок для цветов, имеющий форму цилиндра. Определите радиус этого отверстия так, чтобы горшок для цветов был вписан в конус и имел форму равностороннего цилиндра.

AO=R – радиус основания конуса

Рассмотрим подобные треугольники AKC и AOS.

В них: .

OS=4 (из прямоугольного треугольника AOS с катетом 3 и гипотенузой 5.

KC=2r

Примеры и разбор решения заданий тренировочного модуля

1. В конус, осевым сечением которого является прямоугольный треугольник, вписан равносторонний цилиндр. Найдите отношение площадей полных поверхностей конуса и цилиндра.

Сделаем чертеж осевого сечения

Обозначим радиус цилиндра ЕО= r. Выразим через него все остальные элементы тел вращения.

Так как цилиндр равносторонний, то высота цилиндра равна h=СЕ=2r.

Так как сечение конуса ASB — прямоугольный треугольник и SO — его высота, то SO=OB. То есть высота конуса H равна радиусу R.

Образующая конуса равна L=SA=R .

∆SHD∆DKB∆OSB — прямоугольные равнобедренные треугольники.

Поэтому R=3r, образующая конуса равна SA=3r .

Выразим площади полных поверхностей конуса и цилиндра.

S_п.п.к. =πR(R+L)= π3r(3r+3r)=9πr 2 (1+ )

Теперь найдем отношение: .

Ответ: .

2. Усеченный конус вписан в цилиндр. Найдите площадь полной поверхности усеченного конуса, если радиус цилиндра равен 16, высота равна 6 а радиус меньшего основания усеченного конуса в два раза меньше радиуса цилиндра.

Сделаем чертеж осевого сечения:

O₁B — радиус меньшего основания усеченного конуса.

OC- радиус большего основания усеченного конуса и радиус цилиндра.

BH — высота цилиндра и высота усеченного конуса

По условию OC=2O₁B, ОС=16, BH=6.

Так как OC=2O₁B и ОС=16, то O₁B=8.

Рассмотрим треугольник BHC.

В нем HC=OC-OH=8, BH=6. По теореме Пифагора BC=10.

Теперь нам известен радиус меньшего основания усеченного конуса: он равен 8, радиус большего основания усеченного конуса: он равен 16, образующая усеченного конуса: она равна 10.

Найдем площадь боковой поверхности:

Площадь полной поверхности найдем, прибавив две площади оснований: