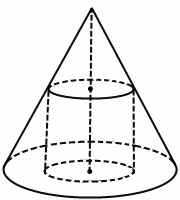
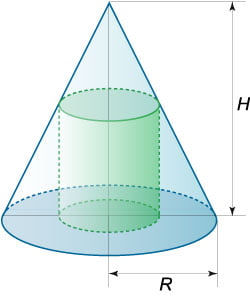
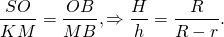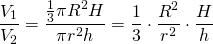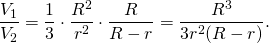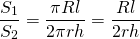В конус вписали цилиндр (7 видео)

В конус вписан цилиндр объема 21. Плоскость верхнего основания этого цилиндра отсекает от исходного конуса усеченный конус объемом 91. Найдите объем исходного конуса.

задан 1 Фев ’15 14:19

Кеша207
270 ● 3 ● 23
95&#037 принятых

Содержание

2 ответа
Здравствуйте
Узнать ещё
Цилиндр вписан в конус
Конус, вписанный в цилиндр
Конус, вписанный в цилиндр
Отношение объемов конуса и описанного около него цилиндра
Математика
Ещё по теме
В конус вписали цилиндр
🎬 Видео

Видео:Пересечение конуса и цилиндраСкачать

2 ответа

Пусть $%h_1$% и $%h_2$% — высоты верхнего и усечённого конусов соответственно. У верхнего конуса и у цилиндра общее основание. При такой же высоте объём верхнего конуса был бы втрое меньше, то есть был бы равен 7, а здесь он равен $%7h_1/h_2$% с учётом отношения высот.

Линейные размеры большого конуса в $%(h_1+h_2):h_1$% раз больше линейных размеров верхнего конуса. Удобно положить $%x=h_2/h_1$%, и тогда получается увеличение объёма в $%(1+x)^3$% раз. На усечённый конус тогда приходится $%(1+x)^3-1$% от объёма верхнего конуса, равного $%7/x$%. Это значит, что $%(1+x)^3-1=91/(7/x)=13x$%. Раскрывая скобки и сокращая на $%x$%, имеем квадратное уравнение $%x^2+3x-10=0$%, положительный корень которого равен $%x=2$%.

Таким образом, верхний конус имеет объём $%7/2$%, а исходный конус больше по объёму в $%(1+x)^3=27$% раз. Получается ответ $%189/2$%.

отвечен 1 Фев ’15 15:20

Пускай $%R$% — радиус основания конуса, $%r$% — радиус основания цилиндра, $%H$% — высота конуса, тогда $%H\frac rR$% — высота «малого» конуса, отсечённого плоскостью верхнего основания цилиндра. По условию $$\pi r^2(H-H\frac rR)=21,\frac13\pi R^2H-\frac13\pi r^2H\frac rR=91.$$ Разделив первое уравнение на второе, получим $$13r^2=R^2+Rr+r^2,$$ $$R=3r.$$ Из второго уравнения $$\frac13\pi R^2H=91/(1-1/27)=189/2.$$ Это и есть искомый объем.

отвечен 1 Фев ’15 15:21

Здравствуйте

Математика — это совместно редактируемый форум вопросов и ответов для начинающих и опытных математиков, с особенным акцентом на компьютерные науки.

Видео:Врезка | Цилиндр и конус | Автор Прохоренко КонстантинСкачать

Узнать ещё

Знание — сила. Познавательная информация

Видео:Цилиндр, конус, шар, 6 классСкачать

Цилиндр вписан в конус

Цилиндр вписан в конус, если одно основание цилиндра лежит в плоскости основания конуса, а окружность другого основания — на боковой поверхности конуса. Конус, соответственно, в этом случае называется описанным около цилиндра.

Оси конуса и вписанного в него цилиндра совпадают. Верхнее основание цилиндра совпадает с сечением конуса плоскостью, параллельной основанию.

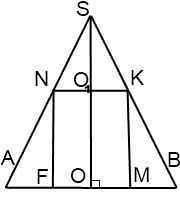
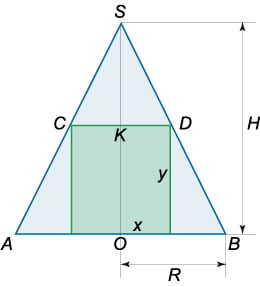
Рассмотрим осевое сечение комбинации тел. Оно представляет собой равнобедренный треугольник с вписанным в него прямоугольником.

Здесь SO=H — высота конуса, OA=OB=R — радиус конуса, OF=OM=r — радиус цилиндра, OO1=h — высота цилиндра, SA=SB=l — образующие конуса, NF=KM=h — образующие цилиндра.

Прямоугольные треугольники SOB и KMB подобны (по общему острому углу B). Из подобия треугольников следует пропорциональность соответствующих сторон:

Найдем отношение объемов конуса и вписанного в него цилиндра:

С учетом предыдущего соотношения для высот конуса и цилиндра, имеем:

Найдем отношение боковой поверхности конуса к боковой поверхности вписанного цилиндра:

Из прямоугольного треугольника SOB по теореме Пифагора

Видео:Как найти объем вписанного конуса? 🔍 #умскул_профильнаяматематика #умскул #никитасалливанСкачать

Конус, вписанный в цилиндр

Видео:Задачи на цилиндр. Вписанный конус - bezbotvyСкачать

Конус, вписанный в цилиндр

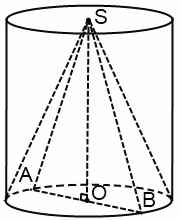
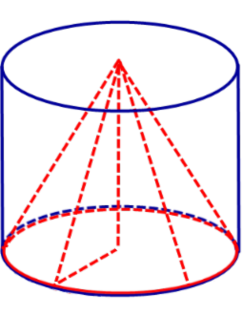
Определение 1. Конусом, вписанным в цилиндр, называют такой конус, у которого основание совпадает с одним из оснований цилиндра, а вершина совпадает с центром другого основания цилиндра (рис. 1).

Определение 2. Если конус вписан в цилиндр, то цилиндр называют описанным около конуса.

Замечание. Высота конуса равна высоте цилиндра, описанного этого конуса.

Утверждение. Около любого конуса можно описать цилиндр.

Доказательство. Для доказательства достаточно построить цилиндр, у которого одно из оснований совпадает с основанием конуса, а плоскость другого основания проходит через вершину конуса.

Читайте также: Изменится ли масса цилиндра

Видео:ЦИЛИНДР. КОНУС. ШАР.Скачать

Отношение объемов конуса и описанного около него цилиндра

Утверждение. Объем конуса в 3 раза меньше объема описанного около него цилиндра.

Доказательство. Пусть радиус основания конуса равен r, а высота конуса равна h. Поскольку цилиндр описан около конуса, то радиус основания цилиндра также равен r, а высота цилиндра равна h. Тогда объем конуса равен

Видео:Лекция № 9 (продолжение 2). Линейчатые поверхности вращения. Конус и цилиндрСкачать

Математика

Ещё по теме

Найдите $ \sin \alpha $ и $ tg \alpha $ , если $ \cos \alpha=-\dfrac12 $ и \( \dfrac ;

Точка $ A( _ >; _ >)=A(5;7) $ — центр окружности. Радиус окружности равен $ 2 $ . Необходимо найти координаты точки $ P $ , полученной поворотом начального радиус-вектора на $ -30<>^\circ $ .

Дан прямоугольный параллелепипед $ ABCDA_1B_1C_1D_1 $ . Доказать, что $ \overrightarrow +\overrightarrow +\overrightarrow =\overrightarrow $

Найти координаты точки на единичной окружности, полученной поворотом точки $ A\left( 1;0 \right) $ на $ -225<>^\circ $ .

Выразить километры в метрах:

Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!

О сайте

На нашем сайте вы найдете множество полезных калькуляторов, конвертеров, таблиц, а также справочных материалов по основным дисциплинам.

Самый простой способ сделать расчеты в сети — это использовать подходящие онлайн инструменты. Воспользуйтесь поиском, чтобы найти подходящий инструмент на нашем сайте.

calcsbox.com

На сайте используется технология LaTeX.
Поэтому для корректного отображения формул и выражений
пожалуйста дождитесь полной загрузки страницы.

Копирование материалов запрещено

Видео:Конус. 11 класс.Скачать

В конус вписали цилиндр

В прямой круговой конус вписан шар. Отношение площади полной поверхности конуса к площади поверхности шара равно 49 : 12. Найти отношение удвоенного объем шара к объему конуса.

Пусть — осевое сечение конуса, О — центр шара, вписанного в этот конус, E — точка касания шара и конуса.

Из условия задачи следует, что — равнобедренный (AB = BC). Очевидно, что точка О лежит на биссектрисе которая также служит медианой и высотой

l — образующая конуса (отрезки AB и BC); R — радиус основания конуса (отрезок AD); H — высота конуса (отрезок BD); r — радиус шара (отрезок OE); — площадь сферы (площадь поверхности шара); — полная поверхность конуса; — объем шара; — объем конуса.

Очевидно, что Рассмотрим прямоугольные треугольники BEO и BDA с общим острым углом OBE. Отсюда: т. е.

Найдем отношение объема шара к объему конуса:

Теперь найдем отношение площади поверхности шара к площади полной поверхности конуса:

Однако, оказалось, что Значит,

Поскольку нам требуется найти отношение удвоенного объема шара к объему заданного конуса, то таким отношением будет 24 : 49.

Объём конуса, вписанного в правильную четырёхугольную пирамиду, равен 3. Найдите объём конуса, описанного около этой пирамиды.

Объемы данных конусов соотносятся как площади их оснований, и, следовательно, как квадраты их диаметров. Диаметр вписанного конуса равен стороне квадрата, диаметр описанного — диагонали квадрата, длина которой равна длины стороны. Поэтому объем описанного конуса в 2 раза больше объема вписанного. Значит, объем конуса, описанного около этой пирамиды, равен 6.

В конус вписан цилиндр так, что нижнее основание цилиндра лежит на основании конуса, а окружность верхнего основания принадлежит боковой поверхности конуса. Объем конуса равен 72.

а) Найти объем цилиндра, верхнее основание которого делит высоту конуса пополам.

б) Найти наибольший объем вписанного цилиндра.

а) Обозначим радиус основания конуса за высоту за за и — радиус и высоту цилиндра. Проведем осевое сечение конуса. В нем верхнее основание цилиндра будет средней линией треугольника, поэтому радиус цилиндра вдвое меньше радиуса конуса. Высота цилиндра — тоже половина высоты конуса. Объем конуса равен: