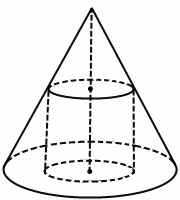
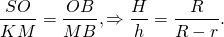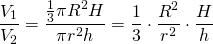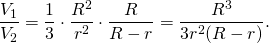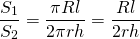Цилиндр вписан в конус, если одно основание цилиндра лежит в плоскости основания конуса, а окружность другого основания — на боковой поверхности конуса. Конус, соответственно, в этом случае называется описанным около цилиндра.
Оси конуса и вписанного в него цилиндра совпадают. Верхнее основание цилиндра совпадает с сечением конуса плоскостью, параллельной основанию.
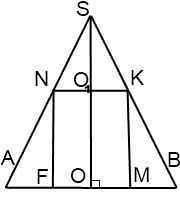
Рассмотрим осевое сечение комбинации тел. Оно представляет собой равнобедренный треугольник с вписанным в него прямоугольником.
Здесь SO=H — высота конуса, OA=OB=R — радиус конуса, OF=OM=r — радиус цилиндра, OO1=h — высота цилиндра, SA=SB=l — образующие конуса, NF=KM=h — образующие цилиндра.
Прямоугольные треугольники SOB и KMB подобны (по общему острому углу B). Из подобия треугольников следует пропорциональность соответствующих сторон:
Найдем отношение объемов конуса и вписанного в него цилиндра:
С учетом предыдущего соотношения для высот конуса и цилиндра, имеем:
Найдем отношение боковой поверхности конуса к боковой поверхности вписанного цилиндра:
Из прямоугольного треугольника SOB по теореме Пифагора
Видео:№550. Осевое сечение конуса — прямоугольный треугольник. Найдите площадь этого сечения, еслиСкачать

Сборник самостоятельных работ по геометрии на тему «Тела вращения»
ГБПОУ города Москвы «Спортивно-педагогический колледж» Департамента спорта и туризма города Москвы; преподаватель математики, информатики и ИКТ: Макеева Елена Сергеевна
Самостоятельная работа № 1 «Цилиндр»
Прямоугольник со сторонами, равными 3*а и 2*а, вращается сначала вокруг одной стороны, затем – вокруг другой. Вычислите отношение площадей полных поверхностей и площадей боковых поверхностей полученных тел вращения.
Через образующую цилиндра проведены две взаимно перпендикулярные плоскости. Площади полученных сечений S1 и S2. Найдите площадь осевого сечения цилиндра.
Плоскость α пересекает основания цилиндра по хордам, дины которых равны 16 см и 12 см. Вычислите тангенс угла наклона плоскости α к плоскостям оснований цилиндра, если радиус оснований цилиндра 10 и высота 30 см.
Прямоугольник со сторонами, равными 4*а и 3*а, вращается сначала вокруг одной стороны, затем – вокруг другой. Вычислите отношение площадей полных поверхностей и площадей боковых поверхностей полученных тел вращения.
Через образующую цилиндра проведены две взаимно перпендикулярные плоскости. Площадь одного из полученных сечений So, площадь осевого сечения цилиндра S. Найдите площадь другого полученного сечения.
Плоскость α пересекает основания цилиндра по хордам, дины которых равны 24 см и 32 см. Вычислите тангенс угла наклона плоскости α к плоскостям оснований цилиндра, если радиус оснований цилиндра 20 и высота 50 см.
Самостоятельная работа № 2 «Конус»
Угол при вершине осевого сечения конуса равен 2α, радиус основания конуса равен R.ь Найдите площадь полной поверхности конуса.
Высота конуса равна h, радиус основания R. Через вершину конуса проведена плоскость, отсекающая от окружности основания дугу в 60o . Вычислите площадь сечения.
Найдите площадь осевого сечения усеченного конуса, если его высота h, образующая L и площадь боковой поверхности S.
Угол между образующей конуса и его основанием равен α, радиус основания конуса R. Найдите площадь полной поверхности конуса.
Высота конуса равна h, радиус основания R. Через вершину конуса проведена плоскость, отсекающая от окружности основания дугу в 90o . Вычислите площадь сечения.
Найдите площадь боковой поверхности усеченного конуса, если его высота h, образующая L и площадь осевого сечения S.
Самостоятельная работа № 3 «Сфера»
Сфера радиуса 6 см касается плоскости треугольника ABC в центре описанной около него окружности. Найдите расстояние от центра сферы до вершин треугольника, если AB=3 см, AC=4 см, BC=5 см.
Определите расстояние между центрами сфер, которые заданы уравнениями x2 + y2 + z2 -2x+6y-4z=5 и x2 +y2+z2+4x+2y+6z=7
Читайте также: Цилиндры алюминиевые урал 650
Сфера проходит через три вершины ромба со стороной, равной 6 см, и углом 60o . Найдите расстояние от центра сферы до четвертой вершины ромба, если радиус сферы равен 10 см.
Сфера радиуса 1,5 см касается плоскости треугольника ABC в центре вписанной в него окружности. Найдите расстояние от центра сферы до сторон треугольника, если AB=6 см, AC=8 см, BC=10 см.
Определите расстояние между центрами сфер, которые заданы уравнениями x2 + y2 + z2 +6x-2y-4z=5 и x2 +y2+z2-2x-6y+4z=11
Сфера проходит через три вершины ромба со стороной, равной 8 см, и углом 60o . Найдите расстояние от центра сферы до четвертой вершины ромба, если радиус сферы равен 10 см.
Самостоятельная работа № 4 «Объемы прямоугольного параллелепипеда, прямой призмы и цилиндра»
Найдите объем прямоугольного параллелепипеда, если площади трех его граней равна 6 см2 , 18 см2 и 12 см2 .
В основании прямой призмы лежит ромб с острым углом α. Меньшая диагональ призмы равна d и составляет с плоскостью основания угол . Вычислите объем призмы.
Центры O1 и O2 оснований цилиндра имеют координаты (0;1;1) и (4;1;1). Одна из точек окружности основания с центром O2 имеет координаты (4;3;-2). Найдите объем цилиндра.
Найдите объем прямоугольного параллелепипеда, если площади трех его граней равна 15 см2 , 45 см2 и 75 см2 .
В основании прямой призмы лежит ромб с острым углом α. Большая диагональ призмы равна d и составляет с плоскостью основания угол . Вычислите объем призмы.
Центры O1 и O2 оснований цилиндра имеют координаты (2;3;3) и (-2;3;3). Одна из точек окружности основания с центром O1 имеет координаты (2;5;-1). Найдите объем цилиндра.
Самостоятельная работа № 5 «Объемы наклонной призмы, пирамиды и конуса»
В наклонной призме боковое ребро равно L, площадь основания S. Угол между плоскостями основания и перпендикулярного боковому ребру сечения равен . Найдите объем призмы.
Стороны оснований правильной усеченной треугольной пирамиды равны a и b (b>a). Боковое ребро наклонено к плоскости основания под углом α. Вычислите объем пирамиды.
Найдите объем и площадь поверхности тела, полученного при вращении треугольника со сторонами 6 см, 25 см и 29 см вокруг прямой, проходящей через вершину меньшего угла треугольника параллельно меньшей его стороне.
В наклонной призме боковое ребро равно L. Угол между плоскостями основания и перпендикулярного боковому ребру сечения равен . Объем призмы равен V. Найдите площадь основания.
Стороны оснований правильной усеченной треугольной пирамиды равны a и b (b>a). Боковая грань наклонена к плоскости основания под углом α. Вычислите объем пирамиды.
Найдите объем и площадь поверхности тела, полученного при вращении треугольника со сторонами 13 см, 14 см и 15 см вокруг прямой, проходящей через вершину среднего по величине угла треугольника параллельно средней его стороне.
Самостоятельная работа № 6 «Объем шара и площадь сферы»
Сфера и два ее взаимно перпендикулярных сечения имеют единственную общую точку. Площади сечений равны 11 π см2 и 14 π см2 . Найдите объем шара и площадь сферы.
Плоскость, перпендикулярная радиусу шара, делит его на части в отношении 2:1, считая от цента шара. Площадь сечения шара этой плоскостью равна 20π см2 . Вычислите объем меньшего шарового сегмента.
Круговой сектор с углом наклона α и хордой aвращается вокруг одного из ограничивающих его радиусов. Найдите объем получившегося шарового сектора.
Сфера и два ее взаимно перпендикулярных сечения имеют единственную общую точку. Площади сечений равны 13 π см2 и 23 π см2 . Найдите объем шара и площадь сферы.
Читайте также: Цилиндр в лампе дневного света
Плоскость, перпендикулярная радиусу шара, делит его на части в отношении 3:1, считая от цента шара. Площадь сечения шара этой плоскостью равна 63 π см2 . Вычислите объем меньшего шарового сегмента.
Круговой сектор с углом наклона α и радиусом R вращается вокруг одного из ограничивающих его радиусов. Найдите объем получившегося шарового сектора.
Самостоятельная работа № 7 «Комбинации круглых тел»
В цилиндр вписан шар радиуса R. Найдите объем и площадь полной поверхности цилиндра.
Вокруг конуса с образующей L и радиусом основания R описана сфера. Определите радиус сферы.
В конус вписан цилиндр, у которого диагонали осевого сечения соответственно параллельны двум образующим конуса. Образующая конуса равна L и составляет с плоскостью основания угол α. Найдите объем цилиндра и площадь его боковой поверхности.
В цилиндр высотой h вписан шар. Найдите объем и площадь полной поверхности цилиндра.
Вокруг конуса с высотой h и радиусом основания R описана сфера. Определите радиус сферы.
В конус вписан цилиндр, у которого диагонали осевого сечения соответственно параллельны двум образующим конуса. Образующая конуса составляет с плоскостью основания угол α, радиус основания конуса равен R. Найдите объем цилиндра и площадь его боковой поверхности.
Самостоятельная работа № 8 «Комбинации многогранников и круглых тел»
Образующая конуса равна L и составляет угол α c плоскостью основания. В конус вписана правильная треугольная пирамида. Найдите объем пирамиды.
Длина стороны основания правильной четырехугольной пирамиды равна a, боковая грань составляет с плоскостью основания угол α. Определите радиус описанной сферы.
В основании прямой призмы лежит прямоугольный треугольник с катетами 2 см и 4 см. Диагональ большей боковой грани образует с основанием угол в 30o . В призму вписан цилиндр. Найдите объем цилиндра.
Высота конуса равна h. Образующая конуса составляет угол α с плоскостью основания. В конус вписана правильная треугольная пирамида. Найдите объем пирамиды.
Боковое ребро правильной четырехугольной пирамиды равно b, боковая грань составляет с плоскостью основания угол α. Определите радиус описанной сферы.
В основании прямой призмы лежит прямоугольный треугольник с катетами 4 см и 6 см. Диагональ большей боковой грани образует с основанием угол в 60o. В призму вписан цилиндр. Найдите объем цилиндра.
Видео:№523. Осевое сечение цилиндра — квадрат, диагональ которого равна 20 см. Найдите: а) высотуСкачать

Геометрия. 11 класс
Конспект урока
Урок №10. Комбинации тел вращения
Перечень вопросов, рассматриваемых в теме:
- комбинации конуса и цилиндра, конуса и усеченного конуса, цилиндра и усеченного конуса, нескольких сфер;
- цилиндр, описанный около конуса, конус, описанный около цилиндра, усеченный конус, описанный около конуса и цилиндра;
- цилиндр, вписанный в конус, конус, вписанный в цилиндр, усеченный конус, вписанный в конус и цилиндр.
Цилиндр вписан в конус, если одно основание цилиндра лежит в плоскости основания конуса, а окружность другого основания — на боковой поверхности конуса. Конус, соответственно, в этом случае называется описанным около цилиндра.
Конус вписан в цилиндр, если основание конуса совпадает с основанием цилиндра, а вершина совпадает с центром другого основания цилиндра. Цилиндр, соответственно, в этом случае называется описанным около конуса.
Конус вписан в другой конус, если его вершина лежит в центре основания второго конуса, а основание лежит на боковой поверхности.
Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. и др. Геометрия. 10–11 классы : учеб. для общеобразоват. организаций : базовый и углубл. уровни – М. : Просвещение, 2014. – 255, сс. 136-147.
Шарыгин И.Ф., Геометрия. 10–11 кл. : учеб. для общеобразоват. учреждений – М.: Дрофа, 2009. – 235, : ил., ISBN 978–5–358–05346–5, сс. 77-84.
Открытые электронные ресурсы:
Теоретический материал для самостоятельного изучения
1. Комбинации цилиндра и конуса
Цилиндр вписан в конус, если одно основание цилиндра лежит в плоскости основания конуса, а окружность другого основания — на боковой поверхности конуса. Конус, соответственно, в этом случае называется описанным около цилиндра.
Читайте также: Признаки неисправного главного тормозного цилиндра ваз 2107
В любой конус можно вписать цилиндр.
Оси конуса и вписанного в него цилиндра совпадают. Верхнее основание цилиндра совпадает с сечением конуса плоскостью, параллельной основанию.
Осевое сечение цилиндра, вписанного в конус — представляет собой равнобедренный треугольник с вписанным в него прямоугольником.
NF=KM=h (l)— образующие цилиндра.
∆SOB∆KMB (по общему острому углу B)


Отношение боковой поверхности конуса к боковой поверхности вписанного цилиндра (через радиусы основания и образующие)


.
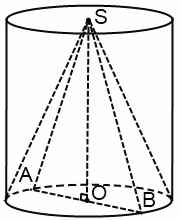
Конус вписан в цилиндр, если основание конуса совпадает с основанием цилиндра, а вершина совпадает с центром другого основания цилиндра. Цилиндр, соответственно, в этом случае называется описанным около конуса.
В любой цилиндр можно вписать конус.
OS — ось цилиндра и ось конуса, высота цилиндра и конуса
OA — радиус конуса и радиус цилиндра
CA=DB=l — образующие цилиндра
∆SOA, ∆SCA, ∆SDB и ∆SOB — прямоугольные
∆SOA=∆SCA, ∆SDB = ∆SOB, поэтому 2S∆ASB=2SACDB.
Отношение боковой поверхности конуса к боковой поверхности описанного около него цилиндра (через радиус основания и высоту)


.
2. Комбинация двух конусов
Конус вписан в другой конус, если его вершина лежит в центре основания второго конуса, а основание лежит на боковой поверхности.
OS — ось конусов, высота большого конуса
OA — радиус большого конуса
В дне кашпо, имеющего форму конуса с площадью боковой поверхности 15π дм и радиусом основания 3 дм, сделано отверстие для того чтобы в него можно было вставить горшок для цветов, имеющий форму цилиндра. Определите радиус этого отверстия так, чтобы горшок для цветов был вписан в конус и имел форму равностороннего цилиндра.
AO=R – радиус основания конуса
Рассмотрим подобные треугольники AKC и AOS.
В них: .
OS=4 (из прямоугольного треугольника AOS с катетом 3 и гипотенузой 5.
KC=2r
Примеры и разбор решения заданий тренировочного модуля
1. В конус, осевым сечением которого является прямоугольный треугольник, вписан равносторонний цилиндр. Найдите отношение площадей полных поверхностей конуса и цилиндра.
Сделаем чертеж осевого сечения
Обозначим радиус цилиндра ЕО= r. Выразим через него все остальные элементы тел вращения.
Так как цилиндр равносторонний, то высота цилиндра равна h=СЕ=2r.
Так как сечение конуса ASB — прямоугольный треугольник и SO — его высота, то SO=OB. То есть высота конуса H равна радиусу R.
Образующая конуса равна L=SA=R .
∆SHD

Поэтому R=3r, образующая конуса равна SA=3r .
Выразим площади полных поверхностей конуса и цилиндра.
Sп.п.к. =πR(R+L)= π3r(3r+3r

Теперь найдем отношение: .
Ответ: .
2. Усеченный конус вписан в цилиндр. Найдите площадь полной поверхности усеченного конуса, если радиус цилиндра равен 16, высота равна 6 а радиус меньшего основания усеченного конуса в два раза меньше радиуса цилиндра.
Сделаем чертеж осевого сечения:
O1B — радиус меньшего основания усеченного конуса.
OC- радиус большего основания усеченного конуса и радиус цилиндра.
BH — высота цилиндра и высота усеченного конуса
По условию OC=2O1B, ОС=16, BH=6.
Так как OC=2O1B и ОС=16, то O1B=8.
Рассмотрим треугольник BHC.
В нем HC=OC-OH=8, BH=6. По теореме Пифагора BC=10.
Теперь нам известен радиус меньшего основания усеченного конуса: он равен 8, радиус большего основания усеченного конуса: он равен 16, образующая усеченного конуса: она равна 10.
Найдем площадь боковой поверхности:
Площадь полной поверхности найдем, прибавив две площади оснований:
🎥 Видео
Видеоурок по математике "Цилиндр"Скачать

ЕГЭ 2022 математика задача 4 вариант 2Скачать

Конус. 11 класс.Скачать

Учимся дома. 11 класс. Геометрия: Решение задач на объемыСкачать

Геометрия, 11 класс ЕМН, СОЧ за III четвертьСкачать

Конус Формулы и СеченияСкачать

Упр.756 ГДЗ Атанасян 10-11 класс по геометрии (Геометрия)Скачать

ЕГЭ|Задание 3 - Цилиндр, конус и шарСкачать

Решение задач КонусСкачать

Усеченный конус. Практическая часть. 11 класс.Скачать

КОНУС егэ по геометрии профильный уровень егэ по математикеСкачать

№521. Докажите, что осевое сечение цилиндра является прямоугольником, две противоположныеСкачать

4.1. Круглые тела. Комбинации круглых тел.Скачать

Урок 19. Задачи на тела вращения из ЕГЭ. Цилиндр, конус, сфера. Стереометрия с нуля.Скачать

Задание 5. ЕГЭ профиль. ЦИЛИНДР.Скачать

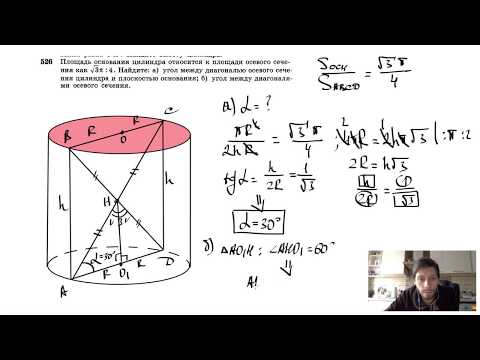
№526. Площадь основания цилиндра относится к площади осевого сечения как √3π:4. Найдите:Скачать
Тела вращенияСкачать