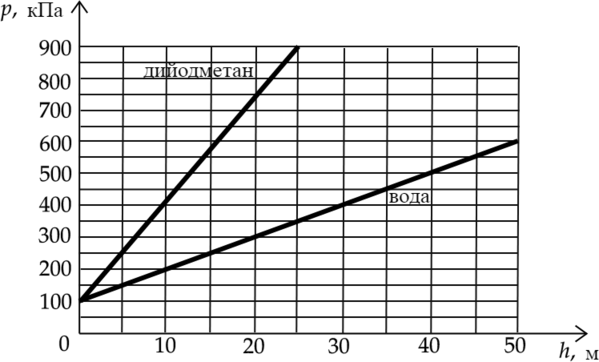
В мерный цилиндр налита жидкость с плотностью (2 видео)

На рисунке представлены графики зависимости давления $p$ от глубины погружения $h$ для двух покоящихся жидкостей: воды и тяжёлой жидкости дийодметана, при постоянной температуре.
Выберите два верных утверждения, согласующихся с приведёнными графиками.
1) Если внутри пустотелого шарика давление равно атмосферному, то в воде на глубине 10 м давления на его поверхность извне и изнутри будут равны друг другу.
2) Плотность керосина 0,82 г/см $^3$ , аналогичный график зависимости давления от глубины для керосина окажется между графиками для воды и дийодметана.
3) В воде на глубине 25 м давление p в 2,5 раза больше атмосферного.
4) С ростом глубины погружения давление в дийодметане возрастает быстрее, чем в воде.
5) Плотность оливкового масла 0,92 г/см $^3$ , аналогичный график зависимости давления от глубины для масла окажется между графиком для воды и осью абсцисс (горизонтальной осью).

Видео:Урок 27 (осн). Плотность. Единицы плотностиСкачать

Полное давление $p$ складывается из атмосферного давления $p_a$ и гидростатического давления столба жидкости: \[p=\rho gh+p_a\] 1) Как видно из графика, давление воды на глубине 10 м принимает значение 200 кПа, что в два раза больше атмосферного давления (Атмосферное давление 100 кПа).
Утверждение 1 – $\color >$
2) Так как плотность керосина меньше чем плотность воды, то его аналогичный график окажется между графиком для воды и осью абсцисс.
Утверждение 2 – $\color >$
3) Давление в воде на глубине 25 м равно 350 кПа, что в 3,5 раза больше атмосферного.
Утверждение 3 – $\color >$
4) Так как прямая давления в дийодметане лежит выше прямой давления в воде, то это означает, что давление в дийодметане возрастает быстрее, чем в воде.
Утверждение 4 – $\color >$
5) Так как плотность оливкого масла меньше чем плотность воды, то его аналогичный график окажется между графиком для воды и осью абсцисс.
Утверждение 5 – $\color >$

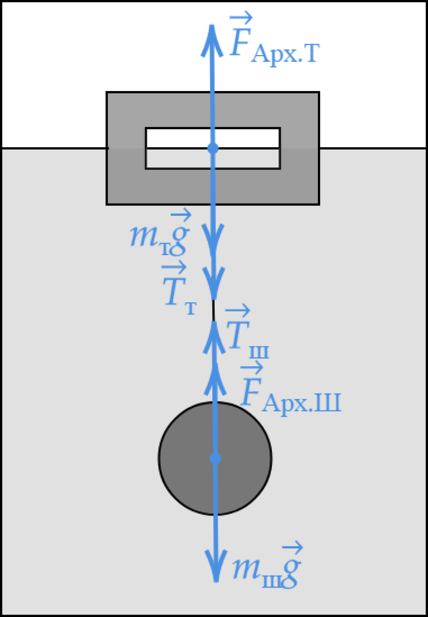
К телу, имеющему внутреннюю герметичную полость, на невесомой нерастяжимой нити привязан сплошной шарик. Система «тело + шарик» плавает в сосуде с жидкостью, не касаясь стенок и дна сосуда. Плотность материала тела и шарика 1,6 г/см $^3$ , плотность жидкости 800 кг/м $^3$ , объём полости составляет 3/4 объёма тела, объём шарика равен 1/4 объёма тела. Исходя из условия задачи, выберите два верных утверждения.
1) Модуль силы Архимеда, действующей на тело, меньше модуля силы Архимеда, действующей на шарик.
2) Модуль силы натяжения нити равен модулю силы тяжести, действующей на шарик.
3) Модуль силы натяжения нити меньше модуля силы Архимеда, действующей на тело.
4) Модуль силы тяжести, действующей на шарик, равен модулю силы тяжести, действующей на тело.
5) Объём погружённой части тела равен четверти объёма этого тела.

Запишем первый закон Ньютона для тела и шарика: \[F_ >-m_ >g-T=0\] \[F_ >-m_ >g+T=0\]
Сложим два уравнения: \[F_ >-m_ >g+F_ >-m_ >g=0\]
Обозначим плотность жидкости $\rho_1$ , плотность материала $\rho_2=2\rho_1$ \[\rho_1gV_1-\rho_2\cdot \frac V_ g+\rho_1 g \cdot \frac V_ -\rho_2\cdot \frac V_ g=0\] \[\rho_1V_1-2\rho_1\cdot \frac V_ +\rho_1 \cdot \frac V_ -2\rho_1\cdot \frac V_ =0\] \[V_1-2\cdot \frac V_ + \frac V_ -2\cdot \frac V_ =0\] \[V_1=\frac V_T\]
Тело плавает, погруженное на 3/4 своего объёма.
1) Сила Архимеда, действующая на тело, равна $\displaystyle F_ >=\rho_1g\frac V_T$ , а сила Архимеда, действующая на шар $\displaystyle F_ >=\rho_1g\frac V_T$ .
Утверждение 1 – $\color >$
2) \[T=m_ >g-F_ >\]
Утверждение 2 – $\color >$
3) \[T=F_ >-m_ >g\]
Утверждение 3 – $\color >$
4) Модуль силы тяжести тела: \[m_ >g=\rho_2\cdot \frac V_ g\] Модуль силы тяжести шарика: \[m_ >g=\rho_2\cdot \frac V_ g\]
Утверждение 4 – $\color >$
5) Объём погружённой части тела равен $\dfrac $ объёма этого тела.
Утверждение 5 – $\color >$

Видео:Easy water experiment: rainbow density towerСкачать

Читайте также: Порядок работы цилиндров ez30

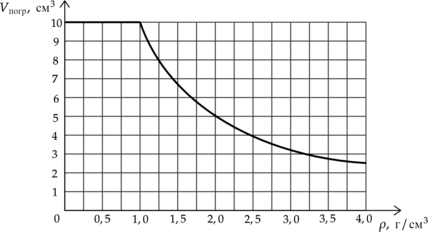
Ученик помещал цилиндр, не удерживая его, в различные жидкости, плотности которых представлены в таблице, и измерял объем погруженной в жидкость части цилиндра $V_\text $ . По результатам измерений он получил зависимость, представленную на графике объема погруженной части цилиндра $V_\text $ от плотности жидкости $\rho$ . Объем цилиндра постоянен и равен $V=10$ см $^3$

\[\begin \hline \text &\text &\text &\text &\text &\text &\text &\text \\ \hline \text &0,71&0,79&1,0&1,26&1,49&2,89&3,25\\ \hline \end \]
На основании анализа приведённого графика выберите два верных утверждения и укажите в ответе их номера.
1) В бензине и воде сила Архимеда, действующая на цилиндр, одинакова.
2) Цилиндр не тонет в глицерине.
3) На цилиндр, погруженный в бромоформ, действует сила Архимеда 200мН.
4) Цилиндр плавает во всех жидкостях, указанных в таблице.
5) При плавании цилиндра в глицирине и бромоформе сила Архимеда, действующая на него, одинакова.

Видео:Лайфхаки ЕГЭ по математике: решения и ответы | Задание 8: цилиндр | Быстрая подготовка к ЕГЭСкачать

1) В бензине и в спирте цилиндр погружен на одинаковый объем. В таком случае сила Архимеда равна \[F_A=\rho gV_\text ,\] где $\rho$ – плотность жидкости, в которую погружено тело.
Но плотность спирта больше плотности бензина, а значит и сила Архимеда, действущая на цилиндр в спирте, больше силы Архимеда, действующей на цилиндр в бензине.
Утверждение 1 – $\color >$
2) Цилиндр тонет при плотности меньше, чем 1 г/см $^3$ , у глицирина плотность 1,26 г/см $^3$ , значит, цилиндр плавает.
Утверждение 2 – $\color >$
3) У бромоформа плотность больше 1 г/см $^3$ , а значит сила Архимеда уравновешивает силу тяжести.
По графику видим, что цилиндр начинает плавать при плотности жидкости 1г/см $^3$ , а значит именно такова плотность материала, из которого он сделан. Откуда сила Архимеда, действующая на цилиндр \[F_A=mg=1\text \cdot 10\text \cdot 10\text =100\text \] Утверждение 3 – $\color >$
4) Нет, при плотности меньше 1 г/см3 цилиндр не плавает.
Утверждение 4 – $\color >$
5) У глицирина и бромоформа плотность больше 1 г/см $^3$ , а значит сила Архимеда уравновешивает силу тяжести и силы Архимеда одинаковы.

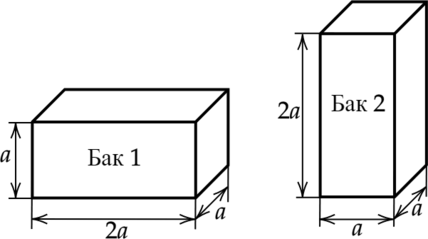
На полу лифта расположены два одинаковых металлических бака, в которых доверху налита вода (см. рисунок).

Из приведённого ниже списка выберите два правильных утверждения и укажите их номера.
1) Давление воды на дно первого бака в 4 раза меньше, чем на дно второго.
2) Первый бак давит на пол лифта с силой, в 2 раза меньшей, чем второй.
3) Сила давления воды на дно первого бака в 2 раза меньше, чем на дно второго.
4) Первый бак оказывает на пол лифта в 2 раза меньшее давление, чем второй.
5) Если лифт начнёт движение вниз с ускорением 2 м/с $^2$ , давление воды на дно баков уменьшится на 20 %.

Видео:🔥 Как измерить ПЛОТНОСТЬ СПИРТА или КОНЦЕНТРАЦИЮ ЛЮБОГО РАСТВОРА.Скачать

Читайте также: Работа цилиндров ваз 2131

1) Давление воды на дно первого бака равно \[\displaystyle p_1=\frac \] где $m$ — масса воды. Давление на дно второго бака \[\displaystyle p_2=\frac \] Видно, что давление $p_2=2p_1$ , следовательно, давление воды на дно первого бака в 2 раза меньше, чем на дно второго бака.
Утверждение 1 – $\color >$
2) Сила давления равна силе тяжести воды. Так как объем одинаковый, значит масса воды в сосудах одинаковая.
Утверждение 2 – $\color >$
3) Утверждение 3 – $\color >$
4) Утверждение 4 – $\color >$
5) При движении лифта вниз с ускорением 2 м/с $^2$ , оно будет компенсировать ускорение свободного падения $g$ , то есть вода будет иметь ускорение свободного падения 10-2=8 м/с $^2$ . В результате сила давления на дно баков будет равна $F=8m$ .
Утверждение 5 – $\color >$

В сосуд с жидкостью погружают маленький датчик манометра, который регистрирует давление, создаваемое только столбом жидкости (без учёта атмосферного давления). На рисунке представлен график зависимости показаний $p$ этого датчика давления от времени $t$ . Известно, что датчик может либо двигаться строго по вертикали вниз со скоростью 1 мм/с, либо покоиться.
На основании анализа приведённого графика выберите два верных утверждения и укажите в ответе их номера.
1) Максимальная глубина погружения датчика давления равна 20 см.
2) В промежутке времени от 50 с до 150 с датчик давления находился на одной и той же глубине.
3) Плотность жидкости, в которую опустили датчик давления, равна 650 кг/м $^3$ .
4) Максимальная глубина погружения датчика давления равна 15 см.
5) Плотность жидкости, в которую опустили датчик давления, равна 1300 кг/м $^3$ .

Видео:7 класс урок №20 Лабораторная работа №3 «Определение плотности жидкостей и твердых тел»Скачать

1) Датчик двигался на промежутках от 0 с до 50 с и от 150 с до 200 с, т. е. глубина погружения $h=1 \cdot (50 + 50 ) = 100$ мм $= 10$ см.
Утверждение 1 – $\color >$
2) Из графика видно, что давление не изменяется в промежутке времени от 50 с до 150 с, это означает что датчик находился на одной и той же глубине, т. е. покоился.
Утверждение 2 – $\color >$
3) Давление столба жидкости: \[p=\rho gh\] Плотность жидкости: \[\rho=\frac

=\frac =1300 \text \]
Утверждение 3 – $\color >$
4) Глубина погружения 10 см
Утверждение 4 – $\color >$
5) Плотность жидкости $\rho=1300$ кг/м $^3$
Утверждение 5 – $\color >$

ГДЗ учебник по физике 7 класс Перышкин. №1 Определение цены деления измеррительного прибора. Номер №1

Цель работы:
Определить цену деления измерительного цилиндра (мензурки), научиться пользоваться им и определять с его помощью объём жидкости.
Приборы и материалы:
Измерительный цилиндр (мензурка), стакан с водой, небольшая колба и другие сосуды.
Указания к работе:
1 . Рассмотрите измерительный цилиндр (рис. 198 ), обратите внимание на его деления. Ответьте на следующие вопросы.
1 )Какой объём жидкости вмещает измерительный цилиндр, если жидкость налита:
а) до верхнего штриха;
б) до первого снизу штриха, обозначенного цифрой, отличной от нуля?
2 )Какой объём жидкости помещается:
а) между 2 −м и 3 −м штрихами, обозначенными цифрами;
б) между соседними (самыми близкими) штрихами мензурки?
2 . Как называется последняя вычисленная вами величина? Как определяют цену деления шкалы измерительного прибора?
Запомните: прежде чем проводить измерения физической величины с помощью измерительного прибора, определите цену деления его шкалы.
3 . Рассмотрите рисунок 7 учебника и определите цену деления изображённой на нём мензурки.
4 . Налейте в измерительный цилиндр воды, определите и запишите, чему равен объём налитой воды.
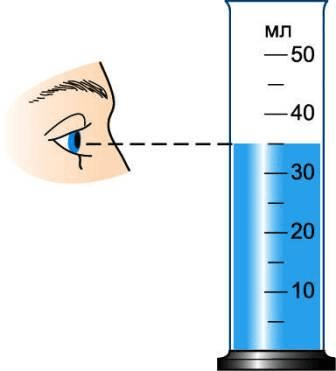
Примечание. Обратите внимание на правильное положение глаза при отсчёте объёма жидкости. Вода у стенок сосуда немного приподнимается, в средней же части сосуда поверхность жидкости почти плоская. Глаз следует направить на деление, совпадающее с плоской частью поверхности (рис. 198 ).
5 . Налейте полный стакан воды, потом осторожно перелейте воду в измерительный цилиндр. Определите и запишите с учётом погрешности, чему равен объём налитой воды. Вместимость стакана будет такой же.
6 . Таким же образом определите вместимость колбы, аптечных склянок и других сосудов, которые находятся на вашем столе.
7 . Результаты измерений запишите в таблицу 6 .

рис. 198 .

рис. 7 . Измерительный цилиндр.
Таблица 6 .

Видео:Перекачка воды с помощью эрлифтаСкачать

Решение

Прежде чем проводить измерения физической величины с помощью измерительного прибора нужно определите цену деления его шкалы.
Для определения цены деления необходимо взять 2 соседних числа, найти их разницу (от большего отнять меньшее), а затем разделить полученное число на количество маленьких штрихов между этими числами.
На шкале цилиндра возьмём, к примеру, числа 20 и 30 .
Таким образом, цена каждого деления будет равна
$\frac = \frac $ = 5 мл.
1 .

Читайте также: Объем цилиндра куба пирамиды

1, а) Если жидкость налита до верхнего штриха, измерительный цилиндр вмещает 50 мл жидкости.
1, б) Если жидкость налита до первого снизу штриха, обозначенного цифрой, отличной от нуля, измерительный цилиндр вмещает 10 мл жидкости.
2, а) Между 2 − м и 3 −м штрихами, обозначенными цифрами, помещается 10 мл жидкости (например, возьмём штрихи 20 мл и 30 мл).
2, б) Между соседними (самыми близкими) штрихами мензурки (например, возьмём штрихи 30 и 35 ), помещается 5 мл жидкости.
2 . Последняя вычисленная нами величина является ценой деления измерительного цилиндра.
3 . На шкале цилиндра возьмём, к примеру, числа 50 и 60 . Количество маленьких штрихов между этими числами − 2 .
Таким образом, цена каждого деления будет равна
$\frac = \frac $ = 5 мл.
4 . Объём налитой воды равен 35 мл или 35 $см^ $ .
5 . Погрешность измерений равна половине цены деления шкалы измерительного прибора. Цена деления цилиндра − 5 мл, следовательно, погрешность измерения равна $\frac $ мл = 2,5 мл.
Объём налитой в полный стакан воды с учётом погрешности будет равен ( 200 ±∆ 2,5 ) мл ( $см^ $ ).
6 .
Таблица 6 .
| № опыта |Название сосуда| Объём жидкости $V_ , см^ $ |Вместимость сосуда, $V_ , см^ $ |
| −−− | −−− | −−− | −−− |
| 1 | стакан | 200 | 200 |
| 2 | колба | 50 | 50 |
| 3 | пузырёк | 30 | 30 |

Вывод. В ходе лабораторной работы мы определелили цену деления измерительного цилиндра, научились им пользоваться и научились с его помощью определять объём жидкости.