Методическая разработка «Тела и поверхности вращения»
Ищем педагогов в команду «Инфоурок»
Методическая разработка по теме
«Тела и поверхности вращения»
РАЗДЕЛ 1. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ………………………. …3-11
РАЗДЕЛ 2. ПРАКТИЧЕСКАЯ ЧАСТЬ…………………..………..12-33
Практическая работа №1: Решение задач по теме «Цилиндр»………12-16
Практическая работа №2: Решение задач по теме «Конус»………..…17-20
Практическая работа №3: Решение задач по теме «Усеченный конус»……………………………………………………………………..….21-23
Практическая работа №4: Решение задач по теме «Нахождение частей сферы и шара»………………………………………………………..……..23-26
Практическая работа №5: Решение задач по теме «Уравнение сферы»………………………………………………………………..………26-29
РАЗДЕЛ 3. ПРОВЕРОЧНАЯ РАБОТА ПО ТЕМЕ «Тела и поверхности вращения»……………………………………………………30-33
РАЗДЕЛ 1. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ.
Определение 1: Цилиндр – это фигура, образованная вращением прямоугольника вокруг одного из его катетов (рис. 1).
Окружности, получаемые при вращении, называются основаниями цилиндра, а прямые их соединяющие – образующими. Прямая, которая проходит через центры окружностей оснований называется осью цилиндра, а совокупность всех образующих – боковой поверхностью цилиндра. Величина называется высотой цилиндра и равна по длине всем его образующим, а – радиусом цилиндра.
прямой цилиндр наклонный цилиндр
Определение 2: Цилиндр, у которого все образующие перпендикулярны к плоскостям, проходящим через основания, называется прямым . В противном же случае он является наклонным (рис. 2).
Рис. 2. Прямой и наклонный цилиндры.
Площадь поверхности цилиндра.
Площадь полной поверхности цилиндра определяется следующим образом:
Найдем теперь формулы для вычисления площадь боковой поверхности и основания.
Так как в основании лежат круги, то очевидно, что
Теорема 1: Площадь боковой поверхности цилиндра определяется как произведение длины окружности, ограничивающей основание цилиндра на его высоту.
Сечение, параллельное осевому сечению
Замечание: цилиндр, осевым сечением которого является квадрат, называется равносторонним цилиндром.
Какой цилиндр называется равносторонним?
Какие фигуры могут получаться в сечении цилиндра?
Какой цилиндр называется прямым? Наклонным?
Видео:11 класс. Геометрия. Объем цилиндра. 14.04.2020Скачать

Чему равна площадь боковой поверхности цилиндра?
Чему равна площадь полной поверхности цилиндра?
Лекция 2 . Конус. Усеченный конус.
Определение 1: Конус – это фигура, образованная вращением прямоугольного треугольника вокруг одного из его катетов (рис. 1).
Круг, из которого составлен конус, называется основанием конуса, r – радиус конуса, точка, не лежащая в плоскости основания – вершиной конуса, прямые, соединяющие вершину с окружностью основания – образующими конуса ( l ), а совокупность всех образующих – боковой поверхностью конуса, а отрезок, соединяющий вершину конуса с центром основания – вершиной конуса ( h ).
Площадь поверхности конуса.
Площадь поверхности цилиндра определяется следующим образом:
Найдем теперь формулы для вычисления площадь боковой поверхности и основания.
Так как в основании лежит круг, то очевидно, что
Теорема 1: Площадь боковой поверхности конуса определяется как половина произведения длины окружности, ограничивающей основание конуса на его образующую.
Определение 2: Усеченный конус – это часть конуса, заключенная между основанием конуса и секущей плоскостью, параллельной основанию (рис. 2).
Теорема 2: Площадь боковой поверхности усеченного конуса определяется как произведение полусуммы длин окружностей, ограничивающих основания на образующую.
Какой конус называется равносторонним?
Что такое усеченный конус?
Какие фигуры могут получаться в сечении конуса?
Чему равна площадь боковой поверхности конуса? Усеченного конуса?
Чему равна площадь полной поверхности конуса? Усеченного конуса?
Определение 1: Сфера – геометрическая фигура в пространстве, состоящая из всех точек, расположенных на равном расстоянии R (радиус сферы) от заданной точки О (центр сферы) (Рис. 1).
Выведем уравнение сферы в системе координат с тремя измерениями. Пусть центр сферы имеет координаты , а радиус сферы равен . Пусть точка с координатами – произвольная точка этой сферы (рис. 2).
Расстояние от центра сферы до точки вычисляется следующим образом
Но, так как лежит на окружности, то по определению 3, получаем . Тогда получим следующее
Уравнение (1) – искомое нами уравнение.
Также можно выделить частный случай для уравнения сферы. Если центр сферы лежит вначале координат, то она имеет следующий вид уравнения:
Площадь сферы определяется следующей формулой:
Определение 2: Шар – геометрическая фигура, ограниченная какой либо сферой, включая саму сферу.
Сечением сферы является окружность (рис. 3)
Если секущая плоскость не проходит через центр сферы, то радиус сечения меньше радиуса сферы.
Видео:Видеоурок по математике "Цилиндр"Скачать

Плоскость сечения, проходящая через центр сферы имеет наибольший радиус и называется большим кругом сферы.
Плоскость большего круга сферы – это плоскость симметрии шара.
Радиусы сечений сферы, равноудаленных от центра сферы, равны.
Определение 3. Плоскость, имеющая со сферой только одну точку, называется касательной плоскостью к сфере (рис. 4).
Читайте также: Как почистить цилиндр бензопилы
Теорема 1: Радиус сферы, проведенный в точку касания сферы и касательной плоскости, перпендикулярен данной плоскости.
Справедлива обратная теорема.
Теорема 2: если радиус сферы перпендикулярен к плоскости, проходящей через его конец, лежащий на сфере, то эта плоскость является касательной плоскостью к сфере.
Шаровой сегмент – часть шара, отсекаемая плоскостью (рис. 5).
Аналогично определяется понятие сферического сегмента.
Площадь сферического сегмента называется шаровым сводом и находится по формуле
Шаровой слой – часть шара, заключенная между параллельными секущими плоскостями (рис. 6).
Сферическая поверхность шарового слоя называется сферическим поясом. Его площадь вычисляется по формуле
Шаровой сектор – часть шара, образованная вращением кругового сектора вокруг оси, проходящей через его центр (рис. 7).
Площадь поверхности шарового сектора определяется по формуле
Как выглядит уравнение сферы в декартовой системе координат?
Что такое шаровой сегмент? Шаровой сектор? Шаровой слой?
Какие фигуры могут получаться в сечении сферы?
Чему равна площадь боковой поверхности сферы и ее частей?
Что такое касательная плоскость к сфере?
Сформулируйте теоремы о касательной плоскости к сфере.
РАЗДЕЛ 2. ПРАКТИЧЕСКАЯ ЧАСТЬ.
Практическая работа №1: Решение задач по теме «Цилиндр»
№ 510 (Сборник задач, Богомолов Н.В.)
В цилиндре проведена параллельно оси плоскость, отсекающая от окружности основания дугу в 60 градусов. Высота цилиндра равна 15 см, расстояние от секущей плоскости до оси цилиндра равно 3 см. Вычислите площадь сечения.
Так как сечение – это прямоугольник, то его площадь находится следующим образом
Рассмотрим треугольник .Здесь
– радиусы цилиндра. Угол – является центральным углом окружности основания цилиндр а, а значит равен дуге , на которую опирается, то есть .
Видео:Объём цилиндраСкачать

Следовательно, треугольник равносторонний треугольник. Отрезок является высотой и медианой, а значит и треугольник –прямоугольный треугольник с прямым углом Н . По теореме Пифагора
№ 517 (Сборник задач, Богомолов Н.В.)
Площадь боковой поверхности цилиндра составляет половину площади его полной поверхности, диагональ осевого сечения равна 5. Найдите площадь полной поверхности цилиндра.
Напомним формулы площадей полной и боковой поверхностей цилиндра
Так как , то получим следующее:
Рассмотрим треугольник . По теореме Пифагора
Задачи для закрепления материала:
Решить из сборника задач Богомолова Н.В. следующие задачи: №507, №515, №518 и №519.
Задания для самостоятельного решения (по вариантам).
Примечание: Вариант выбирается по первой букве вашей фамилии следующим образом: БуквыА-В 1 вариант, Буквы Г-Ж – 2 вариант, Буквы З-Л – 3 вариант, Буквы М-О – 4 вариант , Буквы П-С – 5 вариант , Буквы Т-Ц – 6 вариант , Буквы Ч-Я – 7 вариант.
№ 1. Диагональ осевого сечения цилиндра равна 13 см. а высота равна 12 см. Вычислить площадь основания цилиндра.
№ 2. Радиус основания цилиндра равен 15 см, его высота равна 10 см. Вычислить площадь сечения, параллельного осевому, проведенного от оси на расстоянии 9 см.
№ 3. Площадь осевого сечения цилиндра равна 300. найдите площадь боковой поверхности цилиндра.
№ 4. Образующая равностороннего цилиндра равна 13 см. вычислить площадь боковой поверхности цилиндра.
№ 5. Основанием прямой призмы является прямоугольный треугольник с катетами 7 см 24 см. Длина бокового ребра равна 7 см. вычислите площади осевых сечений вписанного и описанного около призмы цилиндров.
№ 1. Диагональ осевого сечения цилиндра равна 10 см. а высота равна 6 см. Вычислить площадь основания цилиндра.
№ 2. Радиус основания цилиндра равен 13 см, его высота равна 8 см. Вычислить площадь сечения, параллельного осевому, проведенного от оси на расстоянии 5 см.
№ 3. Площадь осевого сечения цилиндра равна 220. найдите площадь боковой поверхности цилиндра.
№ 4. Образующая равностороннего цилиндра равна 22 см. вычислить площадь боковой поверхности цилиндра.
№ 5. Основанием прямой призмы является прямоугольный треугольник с катетами 10 см 24 см. Длина бокового ребра равна 6 см. вычислите площади осевых сечений вписанного и описанного около призмы цилиндров.
№ 1. Диагональ осевого сечения цилиндра равна 10 см. а высота равна 8 см. Вычислить площадь основания цилиндра.
№ 2. Радиус основания цилиндра равен 5 см, его высота равна 12 см. Вычислить площадь сечения, параллельного осевому, проведенного от оси на расстоянии 4 см.
№ 3. Площадь осевого сечения цилиндра равна 130. найдите площадь боковой поверхности цилиндра.
№ 4. Образующая равностороннего цилиндра равна 9 см. вычислить площадь боковой поверхности цилиндра.
Читайте также: Цилиндр вариатора барабана акрос 580
№ 5. Основанием прямой призмы является прямоугольный треугольник с катетами 12 см и 16 см. Длина бокового ребра равна 15 см. вычислите площади осевых сечений вписанного и описанного около призмы цилиндров.
№ 1. Диагональ осевого сечения цилиндра равна 5 см. а высота равна 4 см. Вычислить площадь основания цилиндра.
№ 2. Радиус основания цилиндра равен 10 см, его высота равна 13 см. Вычислить площадь сечения, параллельного осевому, проведенного от оси на расстоянии 6 см.
№ 3. Площадь осевого сечения цилиндра равна 110. найдите площадь боковой поверхности цилиндра.
№ 4. Образующая равностороннего цилиндра равна 4 см. вычислить площадь боковой поверхности цилиндра.
№ 5. Основанием прямой призмы является прямоугольный треугольник с катетами 8 см и 15 см. Длина бокового ребра равна 14 см. вычислите площади осевых сечений вписанного и описанного около призмы цилиндров.
№ 1. Диагональ осевого сечения цилиндра равна 5 см. а высота равна 3 см. Вычислить площадь основания цилиндра.
Видео:Задача, которую боятсяСкачать

№ 2. Радиус основания цилиндра равен 10 см, его высота равна 14 см. Вычислить площадь сечения, параллельного осевому, проведенного от оси на расстоянии 8 см.
№ 3. Площадь осевого сечения цилиндра равна 140. найдите площадь боковой поверхности цилиндра.
№ 4. Образующая равностороннего цилиндра равна 16 см. вычислить площадь боковой поверхности цилиндра.
№ 5. Основанием прямой призмы является прямоугольный треугольник с катетами 9 см и 12 см. Длина бокового ребра равна 8 см. вычислите площади осевых сечений вписанного и описанного около призмы цилиндров.
№ 1. Диагональ осевого сечения цилиндра равна 13 см. а высота равна 12 см. Вычислить площадь основания цилиндра.
№ 2. Радиус основания цилиндра равен 5 см, его высота равна 5 см. Вычислить площадь сечения, параллельного осевому, проведенного от оси на расстоянии 3 см.
№ 3. Площадь осевого сечения цилиндра равна 240. найдите площадь боковой поверхности цилиндра.
№ 4. Образующая равностороннего цилиндра равна 8 см. вычислить площадь боковой поверхности цилиндра.
№ 5. Основанием прямой призмы является прямоугольный треугольник с катетами 5 см и 12 см. Длина бокового ребра равна 10 см. вычислите площади осевых сечений вписанного и описанного около призмы цилиндров.
№ 1. Диагональ осевого сечения цилиндра равна 26 см. а высота равна 24 см. Вычислить площадь основания цилиндра.
№ 2. Радиус основания цилиндра равен 20 см, его высота равна 7 см. Вычислить площадь сечения, параллельного осевому, проведенного от оси на расстоянии 12 см.
№ 3. Площадь осевого сечения цилиндра равна 120. найдите площадь боковой поверхности цилиндра.
№ 4. Образующая равностороннего цилиндра равна 10 см. вычислить площадь боковой поверхности цилиндра.
№ 5. Основанием прямой призмы является прямоугольный треугольник с катетами 3 см и 4 см. Длина бокового ребра равна 12 см. вычислите площади осевых сечений вписанного и описанного около призмы цилиндров.
Справочный материал за курс 9-ти летней школы для решения задачи 5.
Теорема 1: Радиус вписанной в прямоугольный треугольник окружности находится по формуле
где – катеты прямоугольного треугольника, а — его гипотенуза.
Теорема 2: Диаметр описанной около прямоугольного треугольника окружности равен гипотенузе прямоугольного треугольника.
Практическая работа №2: Решение задач по теме «Конус»
№ 526 (Сборник задач, Богомолов Н.В.)
Высота конуса равна Н, угол между высотой и образующей равен 30 градусов. Найдите площадь сечения, проведенного через две образующие, угол между которыми равен 60 градусов.
Сечением является треугольник. Воспользуемся формулой нахождения площади треугольника через синус угла:
Так как две образующие конуса, то
Найдем .По определению косинуса, получим
№ 537 (Сборник задач, Богомолов Н.В.)
Площадь основания конуса составляет , а площадь его осевого сечения — , вычислите площадь его боковой поверхности.
Формула площади боковой поверхности
Так как осевое сечение – это треугольник с высотой то его площадь равна
Так как основание конуса – окружности, то его площадь равна
Найдем образующую по теореме Пифагора
Задания для закрепления материала.
Решить из сборника задач Богомолова Н.В. следующие задачи: №522, №523 и №525.
Видео:№523. Осевое сечение цилиндра — квадрат, диагональ которого равна 20 см. Найдите: а) высотуСкачать

Задачи для самостоятельного решения (по вариантам).
Примечание: Вариант выбирается по первой букве вашей фамилии следующим образом: Буквы А-Д 1 вариант, Буквы Е-Л – 2 вариант, Буквы М-П – 3 вариант, Буквы Р-Ф – 4 вариант , Буквы Х-Я – 5 вариант.
№ 1. В равностороннем конусе (осевое сечение – равносторонний треугольник) радиус основания равен 6. Найти площадь сечения, проведенного через две образующие, угол между которыми равен 30 градусов.
Читайте также: Блок цилиндров ямз 238нд3
№ 2. Образующая конуса равна 40 см и составляет с плоскостью основания угол в 60 градусов. Вычислите площадь основания конуса.
№ 3. Радиус конуса равен 2 см. Найдите радиус сечения конуса, параллельного основанию, которое делит высоту конуса в отношении 2:1.
№ 4. Через вершину конуса с высотой, равной 4 см, под углом 60 градусов к плоскости основания проведена плоскость, отсекающая дугу, равную 90 градусов. Найдите площадь сечения.
№ 5. Площадь осевого сечения конуса равна 120 см.Образующая составляет с плоскостью основания угол в 45 градусов. Вычислите площадь боковой поверхности конуса.
№ 1. В равностороннем конусе (осевое сечение – равносторонний треугольник) радиус основания равен 4. Найти площадь сечения, проведенного через две образующие, угол между которыми равен 30 градусов.
№ 2. Образующая конуса равна 50 см и составляет с плоскостью основания угол в 60 градусов. Вычислите площадь основания конуса.
№ 3. Радиус конуса равен 12 см. Найдите радиус сечения конуса, параллельного основанию, которое делит высоту конуса в отношении 5:1.
№ 4. Через вершину конуса с высотой, равной 2 см, под углом 60 градусов к плоскости основания проведена плоскость, отсекающая дугу, равную 90 градусов. Найдите площадь сечения.
№ 5. Площадь осевого сечения конуса равна 100 см. Образующая составляет с плоскостью основания угол в 45 градусов. Вычислите площадь боковой поверхности конуса.
№ 1. В равностороннем конусе (осевое сечение – равносторонний треугольник) радиус основания равен 8. Найти площадь сечения, проведенного через две образующие, угол между которыми равен 30 градусов.
№ 2. Образующая конуса равна 10 см и составляет с плоскостью основания угол в 60 градусов. Вычислите площадь основания конуса.
№ 3. Радиус конуса равен 10 см. Найдите радиус сечения конуса, параллельного основанию, которое делит высоту конуса в отношении 4:1.
№ 4. Через вершину конуса с высотой, равной 6 см, под углом 60 градусов к плоскости основания проведена плоскость, отсекающая дугу, равную 90 градусов. Найдите площадь сечения.
№ 5. Площадь осевого сечения конуса равна 210 см. Образующая составляет с плоскостью основания угол в 45 градусов. Вычислите площадь боковой поверхности конуса.
№ 1. В равностороннем конусе (осевое сечение – равносторонний треугольник) радиус основания равен 3. Найти площадь сечения, проведенного через две образующие, угол между которыми равен 30 градусов.
№ 2. Образующая конуса равна 20 см и составляет с плоскостью основания угол в 60 градусов. Вычислите площадь основания конуса.
№ 3. Радиус конуса равен 8 см. Найдите радиус сечения конуса, параллельного основанию, которое делит высоту конуса в отношении 2:1.
№ 4. Через вершину конуса с высотой, равной 3 см, под углом 60 градусов к плоскости основания проведена плоскость, отсекающая дугу, равную 90 градусов. Найдите площадь сечения.
№ 5. Площадь осевого сечения конуса равна 180 см. Образующая составляет с плоскостью основания угол в 45 градусов. Вычислите площадь боковой поверхности конуса.
№ 1. В равностороннем конусе (осевое сечение – равносторонний треугольник) радиус основания равен 5. Найти площадь сечения, проведенного через две образующие, угол между которыми равен 30 градусов.
№ 2. Образующая конуса равна 30 см и составляет с плоскостью основания угол в 60 градусов. Вычислите площадь основания конуса.
№ 3. Радиус конуса равен 6 см. Найдите радиус сечения конуса, параллельного основанию, которое делит высоту конуса в отношении 3:1.
№ 4. Через вершину конуса с высотой, равной 5 см, под углом 60 градусов к плоскости основания проведена плоскость, отсекающая дугу, равную 90 градусов. Найдите площадь сечения.
№ 5. Площадь осевого сечения конуса равна 60 см. Образующая составляет с плоскостью основания угол в 45 градусов. Вычислите площадь боковой поверхности конуса.
Практическая работа №3: Решение задач по теме «Усеченный конус»
№ 535 (Сборник задач, Богомолов Н.В.)
Площади оснований усеченного конуса составляют 32 и 2. Высота разделена на три равные части, и через точки деления проведены плоскости параллельно основаниям. Найдите площади сечений.
Достроим усеченный конус, до конуса. Треугольники
Видео:№525. Площадь осевого сечения цилиндра равна 10 м2, а площадь основания — 5 м2.Скачать

Подобны между собой. Следовательно, коэффициент подобия в квадрате равен отношению их площадей. Получаем:
Значит высота конуса разделена на 4 равные части. Тогда
🎥 Видео
№521. Докажите, что осевое сечение цилиндра является прямоугольником, две противоположныеСкачать

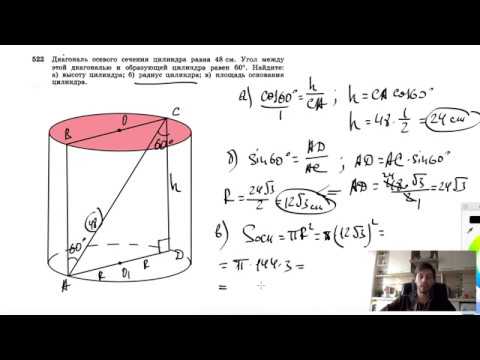
№522. Диагональ осевого сечения цилиндра равна 48 см. Угол между этой диагональю и образующейСкачать
Геометрия 11 класс (Урок№6 - Тела вращения. Цилиндр.)Скачать

11 класс, 15 урок, Площадь поверхности цилиндраСкачать

11 класс, 32 урок, Объем цилиндраСкачать

Осевая симметрия. 6 класс.Скачать

Объем цилиндра. Практическая часть. 11 класс.Скачать

Усеченный цилиндр: проекции сечения, изометрия, развертка поверхностиСкачать

Призма и цилиндр. Практическая часть. 11 класс.Скачать

Объем цилиндра. Урок 13. Геометрия 11 классСкачать

ГЕОМЕТРИЯ 11 класс: Цилиндр. Площадь поверхностиСкачать

Призма и пирамида. Площадь и объем. Вебинар | Математика 10 классСкачать

Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Как найти объем. Принцип Кавальери | Ботай со мной #050 | Борис Трушин |Скачать













