Видео:11 класс, 31 урок, Объем прямой призмыСкачать

В основании прямой призмы прямоугольный треугольник опишите около нее цилиндр
Шар вписан в цилиндр. Площадь полной поверхности цилиндра равна 18. Найдите площадь поверхности шара.
Радиусы шара и основания цилиндра равны. Площадь поверхности цилиндра, с радиусом основания r и высотой 2r равна
Площадь поверхности шара радиуса r равна то есть в 1,5 раза меньше площади поверхности цилиндра. Следовательно, площадь поверхности шара равна 12.
Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 1. Найдите объем параллелепипеда.
Высота параллелепипеда равна высоте вписанного в него цилиндра. Основанием параллелепипеда является квадрат, сторона которого в два раза больше радиуса вписанной в него окружности. Поэтому площадь основания равна 4, а объем параллелепипеда равен
Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 4. Объем параллелепипеда равен 16. Найдите высоту цилиндра.
Высота параллелепипеда равна высоте вписанного в него цилиндра. Основанием параллелепипеда является квадрат, сторона которого в два раза больше радиуса вписанной в него окружности. Поэтому сторона основания равна 8, а площадь основания равна 64. Тогда высота цилиндра равна
Почему получилось 64? Что-то не понятно:(
Длина диаметра цилиндра равна длине стороны квадрата в основании.
В куб вписан шар радиуса 1. Найдите объем куба.
Ребро куба равно диаметру вписанного в него шара, а объем куба равен кубу его ребра. Отсюда имеем:
В основании прямой призмы лежит прямоугольный треугольник с катетами 6 и 8. Боковые ребра равны Найдите объем цилиндра, описанного около этой призмы.
По теореме Пифагора длина гипотенузы треугольника в основании Поскольку гипотенуза является диаметром основания описанного цилиндра, его объем
Видео:🔴 В основании прямой призмы лежит прямоугольный ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 16 | ШКОЛА ПИФАГОРАСкачать

В основании прямой призмы прямоугольный треугольник опишите около нее цилиндр
Шар вписан в цилиндр. Площадь полной поверхности цилиндра равна 18. Найдите площадь поверхности шара.
Радиусы шара и основания цилиндра равны. Площадь поверхности цилиндра, с радиусом основания r и высотой 2r равна
Площадь поверхности шара радиуса r равна то есть в 1,5 раза меньше площади поверхности цилиндра. Следовательно, площадь поверхности шара равна 12.
Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 1. Найдите объем параллелепипеда.
Читайте также: Как найти площадь сечения цилиндра задачи
Высота параллелепипеда равна высоте вписанного в него цилиндра. Основанием параллелепипеда является квадрат, сторона которого в два раза больше радиуса вписанной в него окружности. Поэтому площадь основания равна 4, а объем параллелепипеда равен
Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 4. Объем параллелепипеда равен 16. Найдите высоту цилиндра.
Высота параллелепипеда равна высоте вписанного в него цилиндра. Основанием параллелепипеда является квадрат, сторона которого в два раза больше радиуса вписанной в него окружности. Поэтому сторона основания равна 8, а площадь основания равна 64. Тогда высота цилиндра равна
Почему получилось 64? Что-то не понятно:(
Длина диаметра цилиндра равна длине стороны квадрата в основании.
В куб вписан шар радиуса 1. Найдите объем куба.
Ребро куба равно диаметру вписанного в него шара, а объем куба равен кубу его ребра. Отсюда имеем:
В основании прямой призмы лежит прямоугольный треугольник с катетами 6 и 8. Боковые ребра равны Найдите объем цилиндра, описанного около этой призмы.
По теореме Пифагора длина гипотенузы треугольника в основании Поскольку гипотенуза является диаметром основания описанного цилиндра, его объем
Видео:Геометрия 11 класс (Урок№12 - Объемы прямой призмы и цилиндра.)Скачать

Задание 9 (№ 4963)
В основании прямой призмы лежит прямоугольный треугольник с катетами 4 и 1. Боковые ребра призмы равны 2/π. Найдите объём цилиндра, описанного около этой призмы.
- Объем цилиндра равен произведению его высоты на площадь основания. А площадь основания равна площади круга:V =hSocн =h·π·r 2 .
- Высота цилиндра известна, она равна боковому ребру призмы, то есть 2/π.
- Осталось найти площадь основания.
В основании лежит прямоугольный треугольник, причем по рисунку видим, что гипотенуза данного треугольника проходит через центр основания, тем самым являясь диаметром круга, лежащего в основании цилиндра.
Найдем данную гипотенузу (которая является диаметром) по теореме Пифагора (теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов):
D = – диаметр основания цилиндра.
S = π · ( /2) 2 = 4,25π
- Осталось найти объем цилиндра:
Видео:Площадь поверхности призмы. 11 класс.Скачать

Вписанные и описанные цилиндры.
Презентация для учащихся 11 класса по теме «Комбинация тел» содержит краткую теорию и примеры решения задач на комбинации цилиндра и щара, цилиндра и призмы.Будет полезна при подготовке к ЕГЭ.
Просмотр содержимого документа
«Вписанные и описанные цилиндры.»
Сфера, вписанная в цилиндр
Сфера называется вписанной в цилиндр, если она касается его оснований и боковой поверхности (касается каждой образующей). При этом цилиндр называется описанным около сферы.
Читайте также: Как изготавливаются теплоизоляционные цилиндры
В цилиндр можно вписать сферу, если высота цилиндра равна
Ее центром будет точка O , являющаяся
серединой отрезка, соединяющего центры оснований O 1 и O 2 цилиндра.
В режиме слайдов ответы и решения появляются после кликанья мышкой
Радиус сферы R будет равен
радиусу окружности основания цилиндра.
В цилиндр высоты 2 вписана сфера. Найдите ее радиус.
В цилиндр вписана сфера радиуса 1. Найдите высоту цилиндра.
Радиус основания цилиндра равен 2. Какой должна быть высота цилиндра, чтобы в него можно было вписать сферу?
Высота цилиндра равна 2. Каким должен быть радиус основания цилиндра, чтобы в него можно было вписать сферу?
Осевым сечением цилиндра является прямоугольник со сторонами 1 и 2. Можно ли в этот цилиндр вписать сферу?
Осевым сечением цилиндра является квадрат. Можно ли в этот цилиндр вписать сферу?
Можно ли вписать сферу в цилиндр, осевым сечением которого является ромб?
Можно ли вписать сферу в наклонный цилиндр?
Площадь осевого сечения цилиндра, в который вписана сфера, равна 4 см 2 . Найдите диаметр сферы.
Периметр осевого сечения цилиндра, в который вписана сфера, равен 8 см. Найдите радиус сферы.
Какой наибольший радиус может быть у сферы, помещающейся в цилиндр, радиус основания которого равен 2, и высота 1.
Можно ли сферу радиуса 1 поместить в наклонный цилиндр, радиус основания которого равен 1, а боковое ребро равно 2 и наклонено к плоскости основания под углом 60 о .
Какой наибольший радиус может быть у сферы, помещающейся в наклонный цилиндр, радиус основания которого равен 1, а боковое ребро равно 2 и наклонено к плоскости основания под углом 60 о .
Сфера, описанная около цилиндра
Цилиндр называется вписанным в сферу, если окружности оснований цилиндра лежат на сфере. При этом сфера называется описанной около цилиндра.
Около любого цилиндра можно описать сферу. Ее центром будет точка O , являющаяся серединой отрезка, соединяющего центры оснований O 1 и O 2 цилиндра.
Радиус сферы R вычисляется по формуле
где h – высота цилиндра, r – радиус окружности основания.
В режиме слайдов ответы и решения появляются после кликанья мышкой
Диагональ осевого сечения цилиндра равна 2. Найдите радиус сферы, описанной около этого цилиндра.
Около цилиндра высоты 2 и радиуса основания 1 описана сфера. Найдите ее радиус.
Около цилиндра, радиус основания которого равен 1, описана сфера радиуса 2. Найдите высоту цилиндра.
Около цилиндра, высота которого равна 1, описана сфера радиуса 1. Найдите радиус основания цилиндра.
Читайте также: Как сжать тормозной цилиндр при замене колодок форд фокус 2
Найдите наименьший радиус сферы, в которую помещается наклонный цилиндр, радиус основания которого равен 1, образующая равна 2 и наклонена к плоскости основания под углом 60 о .
Цилиндр, вписанный в призму
Ц илиндр называется вписанным в призму, если е го основания в писаны в основани я цилиндра. При этом , призма называется описанной около цилиндра
В призму можно вписать цилиндр тогда и только тогда, когда
в ее основание можно вписать окружность.
Радиус основания цилиндра равен
радиусу окружности, вписанной в основание призмы.
В режиме слайдов ответы и решения появляются после кликанья мышкой
Можно ли вписать цилиндр в наклонную призму?
Ответ: Да, наклонный цилиндр.
В основании прямой призмы правильный треугольник со стороной 1. Найдите радиус окружности основания цилиндра, вписанного в эту призму.
В основании прямой призмы прямоугольный треугольник с катетами 6 и 8. Найдите радиус окружности основания цилиндра, вписанного в эту призму.
Найдите радиус окружности основания цилиндра, вписанного в единичный куб.
В правильную шестиугольную призму, со стороной основания 1, вписан цилиндр. Найдите радиус окружности основания этого цилиндра.
Цилиндр, описанный около призмы
Ц илиндр называется описанным около призмы, если е го основания о писаны около основани й цилиндра. При этом , п ризма называется вписанной в цилиндр
Около призмы можно описать цилиндр, если около ее оснований можно описать окружности.
Радиус основания цилиндра равен
радиусу окружности, описанной около основания призмы.
В режиме слайдов ответы и решения появляются после кликанья мышкой
Можно ли описать цилиндр около наклонной призмы?
Ответ: Да, наклонный цилиндр.
В основании прямой призмы правильный треугольник со стороной 1. Найдите радиус окружности основания цилиндра, описанного около этой призмы.
В основании прямой призмы прямоугольный треугольник с катетами 6 и 8. Найдите радиус окружности основания цилиндра, описанного около этой призмы.
В основании прямой призмы квадрат со стороной 1. Найдите радиус окружности основания цилиндра, описанного около этой призмы.
Около правильной шестиугольной призмы, со стороной основания 1, описан цилиндр. Найдите радиус окружности основания этого цилиндра.
Около единичного тетраэдра описан цилиндр так, что вершины тетраэдра принадлежат окружностям оснований цилиндра. Найдите радиус основания и высоту цилиндра.
Около единичного октаэдра описан цилиндр так, что две противоположные вершины октаэдра находятся в центрах оснований цилиндра, а остальные вершины принадлежат боковой поверхности цилиндра. Найдите радиус основания и высоту цилиндра.
🔍 Видео
№234. Основанием прямой призмы является прямоугольный треугольник. Через середину гипотенузыСкачать

11 класс. Геометрия. Объем цилиндра. 14.04.2020Скачать

🔴 В бак, имеющий форму прямой призмы, налито ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать

🔴 Радиус основания цилиндра равен 15, а его ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 16 | ШКОЛА ПИФАГОРАСкачать

Объем прямой призмы | Геометрия 11 класс #23 | ИнфоурокСкачать

ЕГЭ|Задание 3 - Цилиндр, конус и шарСкачать

ПРЯМАЯ ПРИЗМА. ЕГЭ. ЗАДАНИЕ 5. СТЕРЕОМЕТРИЯСкачать

№235. Основанием прямой призмы является прямоугольный треугольник с острым углом φ. ЧерезСкачать
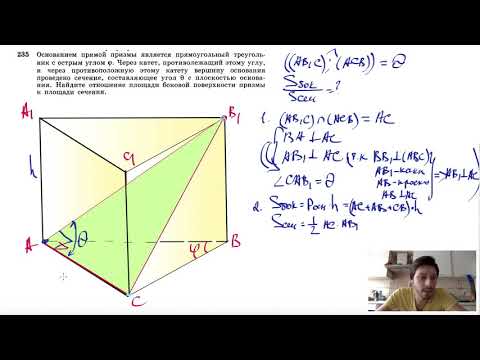
Задание 8 ЕГЭ математика профильный уровеньСкачать

СЛИВ ЕГЭ ПО БАЗЕ 2024Скачать

Призма и пирамида. Площадь и объем. Вебинар | Математика 10 классСкачать

Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Призма и ее элементы, виды призм. 11 класс.Скачать

Задание 54. Чертеж ЛИНИИ ПЕРЕСЕЧЕНИЯ цилиндра и призмы трехгранной Часть 1Скачать
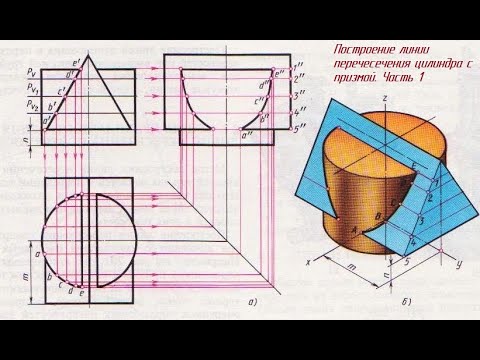
Задача №1 Определение натуральной величины отрезка прямой (АВ) методом прямоугольного треугольникаСкачать

10 класс, 30 урок, ПризмаСкачать






































