В пересечении двух цилиндров получается (5 видео)

Фигура 1.
Есть два (прямых круговых) бесконечных цилиндра (сплошных) одинакового радиуса, оси которых перпендикулярны и пересекаются в одной точке.
Что за фигура получится при их пересечении?

Фигура 2.
То же самое, но для трёх цилиндров (их оси попарно перпендикулярны и пересекются в одной точке).

Голосовать честно, пользоваться можно только бумажкой и ручкой (а не компьютером с каким-нибудь 3ds max )

Кто считает, что представляет себе фигуру 2, — отошлите мне ПМ, сколько по-вашему в этой фигуре граней и рёбер. Что такое грань и ребро — интуитивно понятно. Грань — это гладкий участок поверхности без перемычек, линии негладкости/излома образуют систему кривых на фигуре, часть кривой между двумя узлами — ребро (узел — точка, в которой пересекаются не менее трех кривых). Это согласуется с определением граней и ребер в многогранниках, соответсвенно у фигуры 1 получается граней 4 и рёбер 4.

Видео:Задание 50. Построение ЛИНИИ ПЕРЕСЕЧЕНИЯ ДВУХ ЦИЛИНДРОВСкачать

апд.
На данный момент уже 8 человек проголосовало за то, что могут всё представить. А ПМ пришла только одна. Плиз, не надо врать в этой голосовалке. Если не можете представить — то не голосуйте за первый вариант. Если действительно можете — вам не составит труда посчитать количество ребер и граней, тогда отошлите мне ПМ!

апд.2
учитывая некоторые обтоятельства неправильного понимания условия, напишу: под пересечением понимается логическое И двух фигур. Т. е. надо выкинуть точки, лежащие только в одной фигуре. И останется какая-то конечная фигурка (все точки этой фигуры принадлежат всем трем цилиндрам одновременно), вот надо и узнать, как она выглядит.
А то некоторые понимают это как то, что надо представить просто линии, по которым пересекаются цилиндры

ПЕРЕСЕЧЕНИЯ ДВУХ ТЕЛ ВРАЩЕНИЯ

Линия взаимного пересечения двух тел вращения, как правило, представляет собой пространственную кривую линию (см. рис. 308), но может быть и плоской кривой: окружностью (см. рис. 309, 310, 311) или эллипсом (см. рис. 307,5; 312; 313; 314). В зависимости от взаимного расположения геометрических тел их поверхности могут пересечься по одной или двум замкнутым кривым линиям.

В зависимости от формы поверхности тел вращения линия взаимного пересечения может быть видимой на одной проекции, если пересекаются две проецирующие поверхности (рис. 307); на» двух проекциях, если одно из двух тел имеет проецирующую поверхность (см. рис. 312); на трех проекциях, если оба тела имеют непроецирующие поверхности (рис. 308).

Во всех случаях построение линии взаимного пересечения начинают с нахождения характерных точек, а обводку этой линии — с определения границы видимости и точек, в которых кривая касается очерков поверхностей. Построение промежуточных точек выполняют либо с помощью вспомогательных секущих плоскостей, которые проводят так, чтобы они пересекли одновременно боковые поверхности двух тел по простым линиям: прямым (образующим) и окружностям, либо (при определенных условиях) с помощью вспомогательных сфер. В некоторых случаях, когда одна или обе поверхности являются проецирующими, можно строить точки, принадлежащие линии взаимного пересечения, «по принадлежности», используя образующие и параллели.

Видео:Как построить ЛИНИЮ ПЕРЕСЕЧЕНИЯ двух ЦИЛИНДРОВСкачать

Построение линии взаимного пересечения поверхностей цилиндровначинают со сравнения диаметров их оснований. На рис. 307 изображены три вертикальных цилиндра (А, Б и В) разных диаметров, поверхности которых пересекаются с поверхностью половины горизонтально расположенного цилиндра. Поверхности всех цилиндров проецирующие, поэтому на плоскости Н горизонтальные проекции линий взаимного пересечения совпадают с горизонтальной проекцией боковых поверхностей трех вертикальных цилиндров и проекциями окружностей их оснований. На плоскости W профильные проекции линий взаимного пересечения совпадают с проекцией полуокружности линии основания и профильной проекцией боковой поверхности горизонтально расположенного полуцилиндра. На плоскости V, где боковые поверхности всех цилиндров проецируются в прямоугольники, линии взаимного пересечения изобразятся как кривые линии, которые нужно построить.

Читайте также: Датчик давления в цилиндре для дизеля

Рассмотрим, какая получается линия взаимного пересечения цилиндров в зависимости от соотношения их диаметров. Если пересекаются два цилиндра разных диаметров, то линия их пересечения представляет собой кривую линию, кривизна которой зависит от разности диаметров. Чем больше разность, тем меньше кривизна, и наоборот. При этом изгиб кривой всегда идет в сторону поверхности, имеющей больший диаметр, так как цилиндр с меньшим диаметром как бы проходит через поверхность цилиндра с большим диаметром, вынимая часть его поверхности. Так на рис. 307 цилиндр А проходит сквозь поверхность горизонтального полуцилиндра и изгиб кривой идет как бы по краю отверстия в поверхности горизонтального полуцилиндра. Цилиндр В имеет диаметр больше, чем у горизонтального полуцилиндра, и изгиб линии пересечения идет как бы по краю отверстия в поверхности вертикального цилиндра В.

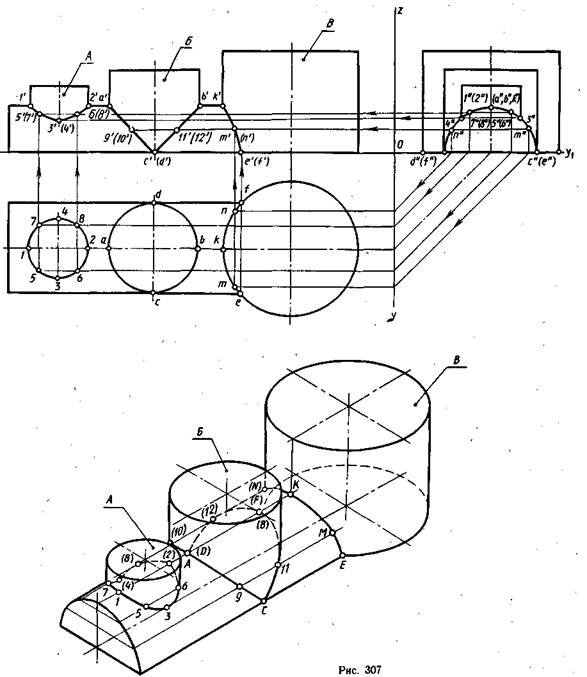Если же диаметры цилиндров одинаковые, то линия взаимного пересечения изображается прямыми линиями, имея в действительности форму эллипсов. На рис. 307 цилиндр Б имеет такой же диаметр, как и горизонтальный полуцилиндр. Линия их взаимного пересечения будет половинками эллипсов, которые изображаются как два отрезка.

Для построения точек, принадлежащих линии взаимного пересечения поверхностей этих цилиндров, сначала отмечают характерные точки 1׳, 2′, а’, Ь’, k», лежащие в пересечении крайних контурных образующих на фронтальной проекции. Затем с помощью линий проекционной связи строят точки 3′ и 4′, с’ и d’. Сначала они отмечаются на профильной проекции (3″, 4″, с» и d») как точки, в которых крайние контурные образующие вертикальных цилиндров пересекаются с контурной полуокружностью основания горизонтального полуцилиндра, с которой совпала профильная проекция его боковой поверхности. Точки е’ и f‘ строят с помощью линий проекционной связи, проведенных с горизонтальной проекции от точек е и f. В этих точках контурные образующие полуцилиндра пересекают боковую поверхность цилиндра В. Промежуточные точки 5′, 6′, 7′, 8′ (цилиндр А) и точки п’, т’ (цилиндр В) построены с помощью линий проекционной связи, проведенных с профильной проекции, где они получились в пересечении промежуточных, произвольно взятых и симметрично расположенных образующих вертикальных цилиндров A и Б с боковой поверхностью горизонтального полуцилиндра (5″, 6″, 7″, 8″, п», т»).

В прямоугольной изометрической проекции видно, что линии взаимного пересечения боковых поверхностей цилиндров A и В с боковой поверхностью горизонтального полуцилиндра представляют собой пространственную кривую. Боковая поверхность цилиндра Б пересекается с боковой поверхностью горизонтально расположенного полуцилиндра по двум плоским кривым — половинкам эллипсов.

Видео:Пересечение двух цилиндров. Инженерная графикаСкачать

Построение линии взаимного пересечения поверхностей вращенияс помощью дополнительных секущих плоскостейвыполнено на рис. 308, где заданы конус и шар. Здесь рассматривается построение линии взаимного пересечения двух

поверхностей, из которых ни одна не является проецирующей. Построение точек, принадлежащих линии пересечения, начинают с определения и построения характерных точек. К ним относятся точки 1—8. Точки 1 и 2 сначала отмечают на фронтальной проекции (1‘ и 2′) как точки пересечения крайних образующих конуса с фронтальным меридианом, лежащим в одной с ними плоскости Q. Затем эти точки с помощью линий проекционной связи строят на горизонтальной и профильной проекциях. Для построения точек 3, 4, 5 и 6 через вершину конуса проводят профильную плоскость Р, которая пересечет поверхность конуса по образующим, а поверхность шара — по окружности. Профильные проекции этих образующих конуса будут крайними, а проекцию окружности, по которой пересекается шар, проводят радиусом, измеренным на фронтальной проекции по следу плоскости Р_ѵ от горизонтальной центровой линии шара до его контурной линии. Профильная проекция окружности пересекается с проекциями крайних образующих конуса в точках 3″, 4″, 5″, 6″. Эти точки будут профильными проекциями искомых точек. С помощью линий проекционной связи строят их фронтальные (3‘, 4′, 5′, 6′) и горизонтальные (3, 4, 5, 6) проекции.

Читайте также: Шевроле ланос сколько цилиндров у двигателя

Точки 7 и 8 строят сначала на горизонтальной проекции как точки пересечения экватора шара с окружностью (параллелью) конуса, лежащими в одной плоскости R. Затем эти точки строят на фронтальной и профильной проекциях с помощью линий проекционной связи.

Точки 9 и 10, 11 и 12, 13 и 14 строят с помощью вспомогательных секущих плоскостей N, Т, М, которые проводят параллельно плоскости Н так, что они пересекают и шар, и конус по окружностям (параллелям). Точки пересечения горизонтальных проекций двух параллелей, лежащих в каждой из плоскостей N, Т, М, определяют горизонтальные проекции искомых промежуточных точек. Так, например, горизонтальные проекции точек 9 и 10 находят в пересечении горизонтальных проекций параллели шара и параллели конуса, лежащих в плоскости N. По горизонтальным проекциям точек 9, 10, 11, 12, 13 и 14 с помощью линий проекционной связи строят их фронтальные и профильные проекции. Затем все точки последовательно от руки соединяют плавной кривой линией и обводят по лекалу. Приступая к обводке построенной линии взаимного пересечения, сначала определяют ее видимость. Так, на фронтальной проекции видимая и невидимая половинки линии сливаются в одну видимую линию. На горизонтальной проекции видимой будет та часть линии, которая находится на фронтальной проекции над экватором шара, а часть линии, расположенная ниже экватора, будет невидимой.

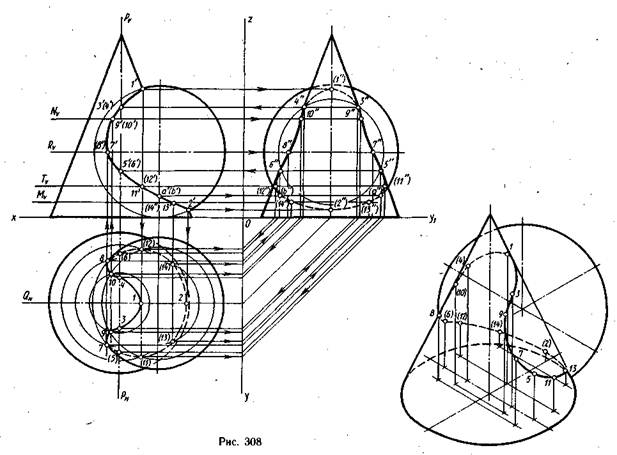Границей видимости являются точки 7 и 8, лежащие на экваторе. На профильной проекции границей видимости будут точки 3″ и 4″, 5″ и 6″‘, лежащие на крайних образующих конуса. На фронтальной проекции эти точки находятся на образующих, совпадающих с осью конуса. Участки кривых линий 4″6″ и 3″5″ будут видимыми.

Видео:Задание 54. Аксонометрия ЛИНИИ ПЕРЕСЕЧЕНИЯ цилиндра и призмы трехгранной Часть 2Скачать

В прямоугольной изометрической проекции линия взаимного пересечения поверхностей конуса и шара построена с помощью вторичных горизонтальных проекций точек 1—14, построенных на изометрической проекции основания конуса, и прямых, параллельных направлению оси Oz, проведенных от вторичных проекций точек. На этих прямых откладывают расстояния, взятые от оси Ох до фронтальных проекций каждой точки.

Границей видимости линии взаимного пересечения будет правая контурная образующая конуса. Точки 1, 3, 9, 7, 5, 11 и 13 и участки кривой линии, лежащие между ними, будут видимыми. Так как поверхности конуса и шара частично пересекают друг друга, то образуется одна замкнутая пространственная кривая линия.

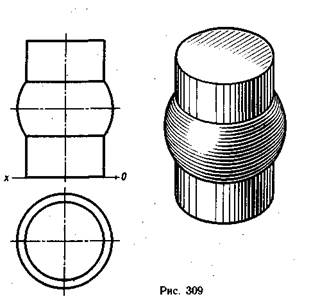
Частные случаи взаимного пересечения двух поверхностей вращенияпоказаны на рис. 309 . 314.

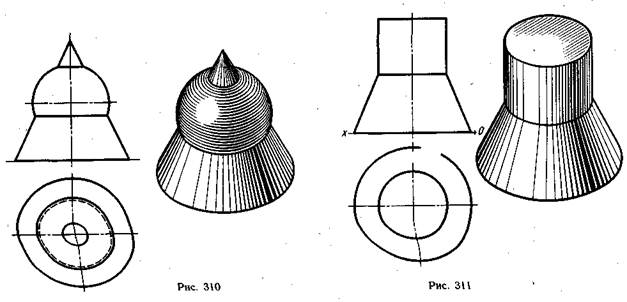Если тела вращения имеют одну общую ось, то линия их взаимного пересечения будет представлять собой окружность — общую параллель для двух тел вращения, которая на ортогональных проекциях будет изображаться на одной проекции как окружность, а на других — как прямая линия (рис. 309—311). Для построения проекций линий пересечения достаточно определить точки взаимного пересечения контурных линий заданных геометрических тел на соответствующих проекциях и соединить их прямой линией

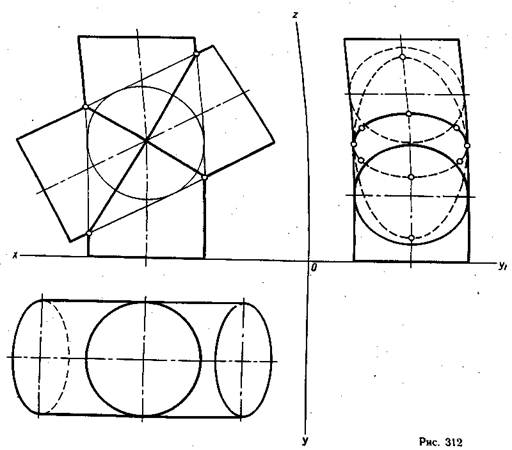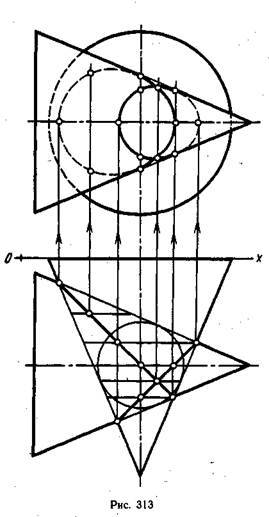
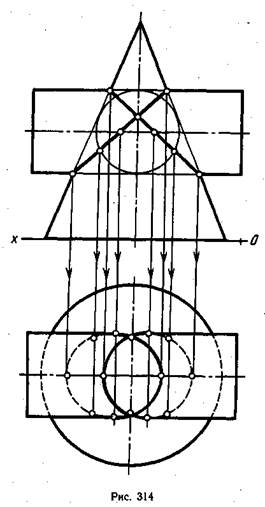
Если у двух поверхностей вращения оси пересекаются и вспомогательная сфера, взятая с центром в точке пересечения этих осей, касается одновременно поверхностей двух заданных тел, то линия их взаимного пересечения распадется на две плоские кривые линии — эллипсы. В ортогональных проекциях пересекающиеся оси двух заданных тел должны быть расположены параллельно какой-либо плоскости проекций, тогда линия их пересечения спроецируется как две пересекающиеся прямые (рис. 312—314). На рис. 312 и 313 линия пересечения распалась на два эллипса различной величины. На рис. 312 они видны на профильной проекции, а на рис. 313 — на горизонтальной проекции. В зависимости от формы поверхности геометрических тел и их взаимного расположения линия пересечения может распасться на два эллипса одинаковой величины, как показано на рис. 314. Эти эллипсы хорошо видны на горизонтальной проекции.

Читайте также: Ремонт тормозного цилиндра 188б

Видео:Пересечение двух цилиндров: объем и площадь поверхности через двойной интегралСкачать

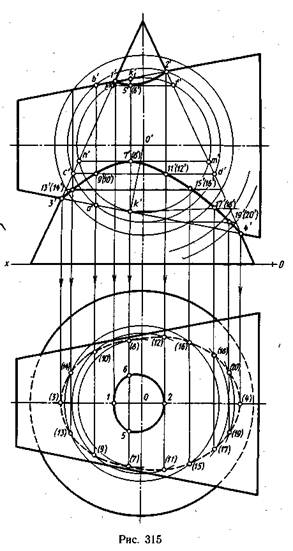
Построение линии взаимного пересечения поверхностей вращения с помощью вспомогательных концентрических сфервыполнено на рис. 315, где заданы два пересекающихся прямых круговых конуса.

Этот способ можно применять в том случае, если пересекаются два тела вращения и их оси пересекаются и расположены параллельно какой-либо плоскости проекций.

Построение линии взаимного пересечения двух тел вращения начинают с определения на одной и построения на других проекциях точек, в которых пересекаются крайние образующие заданных геометрических тел. На рис. 315 этими точками являются точки 1, 2, 3, 4, отмеченные сначала на фронтальной
проекции, а горизонтальные проекции 1, 2, 3, 4 построены с помощью линий проекционной

связи. Остальные точки построены с помощью концентрических сфер. Центр этих сфер берется в точке пересечения осей (точка о’).

Сфера пересекается с каждым из конусов по двум окружностям, которые в данном случае изображаются на фронтальной проекции как отрезки, перпендикулярные осям соответствующих конусов. Для построения этих отрезков необходимо определить точки пересечения контурной линии сферы с контурными линиями каждого конуса и соединить их. Таким образом, две линии пересечения одного конуса со сферой и две линии пересечения второго конуса с той же сферой пересекутся между собой. Точки их пересечения и будут искомыми точками, принадлежащими линии взаимного пересечения. Разберем это на примере построения точек 9′ и 10′, совпадающих на фронтальной проекции. Эти точки получились в результате пересечения проекции а’b’ окружности, по которой пересекается горизонтально расположенный конус со сферой; с проекцией c’d’ окружности, по которой пересекается вертикально расположенный конус с той же сферой. Так же строят и все остальные точки.

Видео:Пересечение поверхностей полусферы и цилиндра. Пошаговое видео. Инженерная графикаСкачать

Количество вспомогательных концентрических сфер определяется их необходимостью. Радиусы сфер берутся произвольно, но при этом нужно учитывать, что проекцию сферы с наименьшим радиусом проводят касательно к образующим большей поверхности, а проекция сферы с наибольшим радиусом не должна проходить дальше, чем расположена наиболее удаленная крайняя точка, лежащая в пересечении очерковых образующих. На рис. 315 такой точкой является точка 4′. Для определения радиуса наименьшей сферы из точки о’ опускают перпендикуляр на крайнюю образующую и получают точку касания k’. Расстояние ok’ и будет искомым радиусом. Фронтальная проекция горизонтально расположенного конуса имеет с проекцией касательной сферы общую окружность k’k׳₁, а проекция вертикально расположенного конуса пересекается с проекцией сферы наименьшего радиуса по двум окружностям (проекции е’f׳ и п’т’), которые пересекаются с проекцией k’k׳₁ окружности в точках 5′, 6′ и 7′, 8′.

На горизонтальной проекции точки 5. 20 строят с помощью линий проекционной связи, проведенных от фронтальных проекций этих точек до пересечения с проекциями окружностей, по которым концентрические сферы пересекаются с поверхностью вертикально расположенного конуса.

Точки, построенные на фронтальной и горизонтальной проекциях, соединяют от руки и обводят по лекалу, предварительно определив их видимость. На фронтальной проекции (рис. 315) невидимая часть линии пересечения совпадает с видимой частью этой линии.

§38. ПОСТРОЕНИЕ ЧЕРТЕЖЕЙ МОДЕЛЕЙ,

📸 Видео

Линия пересечения двух поверхностей конус и цилиндр (Метод секущих плоскостей)Скачать

Линия пересечения двух поверхностей вращения (Метод вспомогательных сфер)Скачать

Задание 51. Как начертить ЛИНИЮ ПЕРЕСЕЧЕНИЯ ПРИЗМ.Скачать

Пересечение конуса и цилиндраСкачать

ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТЕЙ ДВУХ ЦИЛИНДРОВ. Начертательная геометрия [crossing two cylinders]Скачать

Как построить ЛИНИИ ПЕРЕСЕЧЕНИЯ трехгранной ПРИЗМЫ С ЦИЛИНДРОМСкачать

Задание 54. Чертеж ЛИНИИ ПЕРЕСЕЧЕНИЯ цилиндра и призмы трехгранной Часть 1Скачать

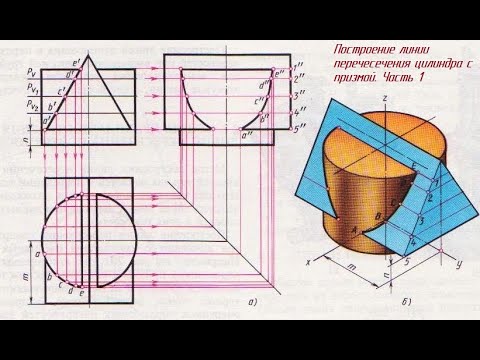
Пересечение двух поверхностей вращения - конуса и цилиндраСкачать

Лекция 12. Пересечение поверхностей метод плоскостейСкачать

Взаимное пересечение поверхностей/ (способ секущих плоскостей)/ Задача 49./ Рабочая тетрадь.Скачать

Линия пересечения конуса и цилиндра (метод концентричных секущих сфер)Скачать

85КБ. Пересечение поверхностей цилиндра и полусферы. Определение видимости.Скачать

Пересечение двух многогранниковСкачать