В правильную четырехугольную пирамиду вписан цилиндр найдите площадь его боковой (2 видео)

Содержание

Решение №2305 Цилиндр вписан в правильную четырёхугольную призму. Радиус основания и высота цилиндра равны 3.
В правильную четырехугольную пирамиду вписан цилиндр найдите площадь его боковой
В правильную четырехугольную пирамиду вписан цилиндр найдите площадь его боковой
В правильную четырехугольную пирамиду вписан цилиндр найдите площадь его боковой
🎥 Видео

Видео:#130. Задание 8: комбинация телСкачать

Решение №2305 Цилиндр вписан в правильную четырёхугольную призму. Радиус основания и высота цилиндра равны 3.

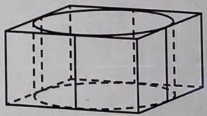
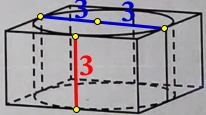
Цилиндр вписан в правильную четырёхугольную призму. Радиус основания и высота цилиндра равны 3. Найдите площадь боковой поверхности призмы.

Источник: Ященко ЕГЭ 2022 (36 вар)

Правильной четырёхугольной призмой – называется шестигранник, в основаниях которого находятся 2 квадрата, а боковые грани представлены прямоугольниками.
Площадь боковой поверхности данной призмы – это площадь 4-х равных прямоугольников.
Длина прямоугольника равна диаметру цилиндра, ширина прямоугольника равна высоте цилиндра.

Найдём площадь боковой поверхности призмы:

S_{бок. поверх.} = 4·S_{прямоугольника} = 4· h ·( r + r ) = 4·3·(3 + 3) = 4·3·6 = 72

Видео:ЕГЭ 2022 математика задача 4 вариант 2Скачать

В правильную четырехугольную пирамиду вписан цилиндр найдите площадь его боковой

Шар вписан в цилиндр. Площадь полной поверхности цилиндра равна 18. Найдите площадь поверхности шара.

Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 1. Найдите объем параллелепипеда.

Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 4. Объем параллелепипеда равен 16. Найдите высоту цилиндра.

В куб вписан шар радиуса 1. Найдите объем куба.

В основании прямой призмы лежит прямоугольный треугольник с катетами 6 и 8. Боковые ребра равны Найдите объем цилиндра, описанного около этой призмы.

В основании прямой призмы лежит квадрат со стороной 2. Боковые ребра равны Найдите объем цилиндра, описанного около этой призмы.

Цилиндр и конус имеют общие основание и высоту. Объём конуса равен 25. Найдите объём цилиндра.

Из единичного куба вырезана правильная четырехугольная призма со стороной основания 0,5 и боковым ребром 1. Найдите площадь поверхности оставшейся части куба.

Цилиндр и конус имеют общие основание и высоту. Найдите объем конуса, если объем цилиндра равен 150.

Объём куба, описанного около сферы, равен 216. Найдите радиус сферы.

Конус описан около правильной четырехугольной пирамиды со стороной основания 4 и высотой 6. Найдите его объем, деленный на

Во сколько раз объем конуса, описанного около правильной четырехугольной пирамиды, больше объема конуса, вписанного в эту пирамиду?

В куб с ребром 3 вписан шар. Найдите объем этого шара, деленный на

Около куба с ребром описан шар. Найдите объем этого шара, деленный на

Читайте также: Шток главного цилиндра сцепления 21213

Вершина A куба с ребром 1,6 является центром сферы, проходящей через точку A₁. Найдите площадь S части сферы, содержащейся внутри куба. В ответе запишите величину

Видео:Стереометрия, номер 10.1Скачать

В правильную четырехугольную пирамиду вписан цилиндр найдите площадь его боковой

Шар вписан в цилиндр. Площадь полной поверхности цилиндра равна 18. Найдите площадь поверхности шара.

В куб вписан шар радиуса 1. Найдите объем куба.

Цилиндр и конус имеют общие основание и высоту. Объём конуса равен 25. Найдите объём цилиндра.

Цилиндр и конус имеют общие основание и высоту. Найдите объем конуса, если объем цилиндра равен 150.

Объём куба, описанного около сферы, равен 216. Найдите радиус сферы.

В куб с ребром 3 вписан шар. Найдите объем этого шара, деленный на

Около куба с ребром описан шар. Найдите объем этого шара, деленный на

Видео:Стереометрия. В правильную четырехугольную призму вписан круглый цилиндра. Найдите высоту цилиндраСкачать

В правильную четырехугольную пирамиду вписан цилиндр найдите площадь его боковой

БАЗА ЗАДАНИЙ

Задание № 5. Стереометрия.

81. Около шара описан цилиндр, площадь поверхности которого равна 18. Найдите площадь поверхности шара.

82. Шар вписан в цилиндр. Площадь поверхности шара равна 48. Найдите площадь полной поверхности цилиндра.

83. Шар вписан в цилиндр. Объем шара равен 6. Найдите объем цилиндра.

84. В куб с ребром 3 вписан шар. Найдите объем этого шара, деленный на π.

85. Объем прямоугольного параллелепипеда, описанного около сферы, равен 216. Найдите радиус сферы.

86. Прямоугольный параллелепипед описан около единичной сферы. Найдите его площадь поверхности.

Читайте также: Тагаз вега рабочий цилиндр сцепления

87. Первая цилиндрическая кружка вдвое выше второй, зато вторая в три раза шире. Найдите отношение объёма второй кружки к объёму первой.

88. Объем первой цилиндрической кружки равен 12. У второй кружки высота в два раза меньше, а радиус основания в три раза больше. Найдите объём второй кружки.

89. Во сколько раз увеличится объем шара, если его радиус увеличить в три раза?

90. Площадь большого круга шара равна 3. Найдите площадь поверхности шара.

91. Объем шара равен 288 π. Найдите площадь его поверхности, деленную на π.

92. Радиусы двух шаров равны 6, 8. Найдите радиус шара, площадь поверхности которого равна сумме площадей их поверхностей.

93. Объем первого шара в 27 раз больше объема второго. Во сколько раз площадь поверхности первого шара больше площади поверхности второго.

96. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

97. Найдите площадь поверхности многогранника, изображенного на рисунке.

98. На рисунке изображен многогранник, все двугранные углы прямые. Найдите квадрат расстояния между вершинами A и C 3 .

99. Объем тетраэдра равен 19. Найдите объем многогранника, вершинами которого являются середины сторон данного тетраэдра.

100. Площадь поверхности тетраэдра равен 12. Найдите площадь поверхности многогранника, вершинами которого являются середины сторон данного тетраэдра.

101. Во сколько раз увеличится площадь поверхности октаэдра, если все его ребра увеличить в 3 раза?

102. Найдите объем пространственного креста, изображенного на рисунке и составленного из единичных кубов.

103. Найдите площадь поверхности пространственного креста, изображенного на рисунке и составленного из единичных кубов.

104. Ребра тетраэдра равны 1. Найдите площадь сечения, проходящего через середины четырех его ребер.

105. Объем треугольной пирамиды SABC равен 15. Плоскость проходит через сторону AB основания этой пирамиды и пересекает противоположное боковое ребро в точке D, делящей ребро SC в отношении 1: 2, считая от вершины S. Найдите объем пирамиды DABC.

106. От треугольной пирамиды, объем которой равен 12, отсечена треугольная пирамида плоскостью, проходящей через вершину пирамиды и среднюю линию основания. Найдите объем отсеченной треугольной пирамиды.

107. От призмы ABCA 1 B 1 C 1 , объем которой равен 6, отсечена треугольная пирамида C 1 ABC. Найдите объем оставшейся части.

108. Площадь осевого сечения цилиндра равна 4. Найдите площадь боковой поверхности цилиндра, деленную на π.

109. Найдите объем цилиндра, площадь основания которого равен 1, а образующая равна 6 и наклонена к плоскости основания под углом 30.

Читайте также: Измерения объема жидкостей с помощью мерного цилиндра

110. Конус описан около правильной четырехугольной пирамиды со стороной основания 4 и высотой 6. Найдите его объем, деленный на π.

111. Во сколько раз объем конуса, описанного около правильной четырехугольной пирамиды, больше объема конуса, вписанного в эту пирамиду?

112. В основании прямой призмы лежит квадрат со стороной 2. Боковые ребра равны 2/ π. Найдите объем цилиндра, описанного около этой призмы.

113. Найдите площадь боковой поверхности правильной треугольной призмы, вписанной в цилиндр, радиус основания которого равен 2√3, а высота равна 2.

114. Найдите площадь боковой поверхности правильной треугольной призмы, описанной около цилиндра, радиус основания которого равен √3, а высота равна 2.

115. Найдите площадь боковой поверхности правильной шестиугольной призмы, описанной около цилиндра, радиус основания которого равен √3, а высота равна 2.

116. Около куба с ребром √3 описан шар. Найдите объем этого шара, деленный на π.

117. Боковые ребра треугольной пирамиды взаимно перпендикулярны, каждое из них равно 3. Найдите объем пирамиды.

118. Основанием пирамиды служит прямоугольник, одна боковая грань перпендикулярна плоскости основания, а три другие боковые грани наклонены к плоскости основания под углом 60°. Высота пирамиды равна 6. Найдите объем пирамиды.

119. Найдите объем призмы, в основаниях которой лежат правильные шестиугольники со сторонами 2, а боковые ребра равны 2√3 и наклонены к плоскости основания под углом 30°.

120. Из единичного куба вырезана правильная четырехугольная призма со стороной основания 0,5 и боковым ребром 1. Найдите площадь поверхности оставшейся части куба.

121. В треугольной призме две боковые грани перпендикулярны. Их общее ребро равно 10 и отстоит от других боковых ребер на 6 и 8. Найдите площадь боковой поверхности этой призмы.

122. В правильной четырёхугольной призме ABCDA 1 B 1 C 1 D 1 известно, что BD₁ =2AD. Найдите угол между диагоналями DB₁ и CA₁. Ответ дайте в градусах.

123. В прямоугольном параллелепипеде ABCDA 1 B 1 C 1 D 1 ребро АВ=2, ребро AD= √5, ребро AA₁=2. Точка К – середина ребра BB₁. Найдите площадь сечения,проходящего через точки A₁, D₁ и K.

124. В прямоугольном параллелепипеде ABCDA 1 B 1 C 1 D 1 ребро АВ=8, ребро AD=6, ребро AA 1 =21. Найдите синус угла между прямыми CD и A 1 C 1 .

125. Найдите объем правильной треугольной пирамиды, стороны основания которой равны 1, а высота равна √3.

126. Одна из граней прямоугольного параллелепипеда – квадрат. Диагональ параллелепипеда равна √8 и образует с плоскостью этой грани угол 45°. Найдите объем параллелепипеда.