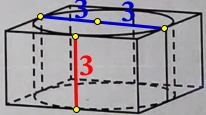
В правильную треугольную призму объем которой равен 36 вписан цилиндр (8 видео)

Содержание

Решение №2305 Цилиндр вписан в правильную четырёхугольную призму. Радиус основания и высота цилиндра равны 3.
В правильную треугольную призму объем которой равен 36 вписан цилиндр
В правильную треугольную призму объем которой равен 36 вписан цилиндр
📹 Видео

Видео:11 класс. Контрольная №4 (из 6). Тема: Объем призмы, цилиндра и конуса. Решение с советами! :)Скачать

Решение №2305 Цилиндр вписан в правильную четырёхугольную призму. Радиус основания и высота цилиндра равны 3.

Цилиндр вписан в правильную четырёхугольную призму. Радиус основания и высота цилиндра равны 3. Найдите площадь боковой поверхности призмы.

Источник: Ященко ЕГЭ 2022 (36 вар)

Правильной четырёхугольной призмой – называется шестигранник, в основаниях которого находятся 2 квадрата, а боковые грани представлены прямоугольниками.
Площадь боковой поверхности данной призмы – это площадь 4-х равных прямоугольников.
Длина прямоугольника равна диаметру цилиндра, ширина прямоугольника равна высоте цилиндра.

Найдём площадь боковой поверхности призмы:

S_{бок. поверх.} = 4·S_{прямоугольника} = 4· h ·( r + r ) = 4·3·(3 + 3) = 4·3·6 = 72

Видео:Призма и цилиндр. Практическая часть. 11 класс.Скачать

В правильную треугольную призму объем которой равен 36 вписан цилиндр

При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.

Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.

Даны два шара. Радиус первого шара в 2 раза больше радиуса второго. Во сколько раз площадь поверхности первого шара больше площади поверхности второго?

Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 2. Площадь поверхности параллелепипеда равна 16. Найдите его диагональ.

Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

Найдите объем многогранника, вершинами которого являются точки правильной треугольной призмы площадь основания которой равна 3, а боковое ребро равно 2.

Найдите объем параллелепипеда если объем треугольной пирамиды равен 3.

Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 5, а высота — 10.

Найдите объем многогранника, изображенного на рисунке (все двугранные углы многогранника прямые).

Из единичного куба вырезана правильная четырехугольная призма со стороной основания 0,5 и боковым ребром 1. Найдите площадь поверхности оставшейся части куба.

Площадь поверхности куба равна 2592. Найдите его диагональ.

От треугольной призмы, объем которой равен 6, отсечена треугольная пирамида плоскостью, проходящей через сторону одного основания и противоположную вершину другого основания. Найдите объем оставшейся части.

Читайте также: Цилиндры для изоляции трубопроводов размеры

Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Найдите объем правильной шестиугольной призмы, стороны основания которой равны 1, а боковые ребра равны

Найдите объем многогранника, вершинами которого являются точки A, B, C, D, A₁, B₁, C₁, D₁ правильной шестиугольной призмы ABCDEFA₁B₁C₁D₁E₁F₁, площадь основания которой равна 6, а боковое ребро равно 2.

Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Объем конуса равен 16. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.

Боковые ребра треугольной пирамиды взаимно перпендикулярны, каждое из них равно 3. Найдите объем пирамиды.

Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите

Во сколько раз уменьшится объем конуса, если его высота уменьшится в 3 раза, а радиус основания останется прежним?

Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Найдите объем V конуса, образующая которого равна 2 и наклонена к плоскости основания под углом 30°. В ответе укажите

Площадь поверхности правильной треугольной призмы равна 6. Какой станет площадь поверхности призмы, если все её рёбра увеличатся в три раза, а форма останется прежней?

Если каждое ребро куба увеличить на 1, то его площадь поверхности увеличится на 54. Найдите ребро куба.

Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 2, 3. Найдите его площадь поверхности.

Цилиндр описан около шара. Объем шара равен 24. Найдите объем цилиндра.

Объем шара равен 288 Найдите площадь его поверхности, деленную на

Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем шара равен 28. Найдите объем конуса.

Найдите объем многогранника, вершинами которого являются точки правильной шестиугольной призмы площадь основания которой равна 6, а боковое ребро равно 2.

Видео:ЕГЭ 2022 математика задача 4 вариант 2Скачать

В правильную треугольную призму объем которой равен 36 вписан цилиндр

БАЗА ЗАДАНИЙ

Задание № 5. Стереометрия.

81. Около шара описан цилиндр, площадь поверхности которого равна 18. Найдите площадь поверхности шара.

82. Шар вписан в цилиндр. Площадь поверхности шара равна 48. Найдите площадь полной поверхности цилиндра.

83. Шар вписан в цилиндр. Объем шара равен 6. Найдите объем цилиндра.

84. В куб с ребром 3 вписан шар. Найдите объем этого шара, деленный на π.

Читайте также: Сечение цилиндра плоскостью параллельной оси отсекает от окружности основания дугу

85. Объем прямоугольного параллелепипеда, описанного около сферы, равен 216. Найдите радиус сферы.

86. Прямоугольный параллелепипед описан около единичной сферы. Найдите его площадь поверхности.

87. Первая цилиндрическая кружка вдвое выше второй, зато вторая в три раза шире. Найдите отношение объёма второй кружки к объёму первой.

88. Объем первой цилиндрической кружки равен 12. У второй кружки высота в два раза меньше, а радиус основания в три раза больше. Найдите объём второй кружки.

89. Во сколько раз увеличится объем шара, если его радиус увеличить в три раза?

90. Площадь большого круга шара равна 3. Найдите площадь поверхности шара.

91. Объем шара равен 288 π. Найдите площадь его поверхности, деленную на π.

92. Радиусы двух шаров равны 6, 8. Найдите радиус шара, площадь поверхности которого равна сумме площадей их поверхностей.

93. Объем первого шара в 27 раз больше объема второго. Во сколько раз площадь поверхности первого шара больше площади поверхности второго.

96. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

97. Найдите площадь поверхности многогранника, изображенного на рисунке.

98. На рисунке изображен многогранник, все двугранные углы прямые. Найдите квадрат расстояния между вершинами A и C 3 .

99. Объем тетраэдра равен 19. Найдите объем многогранника, вершинами которого являются середины сторон данного тетраэдра.

100. Площадь поверхности тетраэдра равен 12. Найдите площадь поверхности многогранника, вершинами которого являются середины сторон данного тетраэдра.

101. Во сколько раз увеличится площадь поверхности октаэдра, если все его ребра увеличить в 3 раза?

102. Найдите объем пространственного креста, изображенного на рисунке и составленного из единичных кубов.

103. Найдите площадь поверхности пространственного креста, изображенного на рисунке и составленного из единичных кубов.

104. Ребра тетраэдра равны 1. Найдите площадь сечения, проходящего через середины четырех его ребер.

105. Объем треугольной пирамиды SABC равен 15. Плоскость проходит через сторону AB основания этой пирамиды и пересекает противоположное боковое ребро в точке D, делящей ребро SC в отношении 1: 2, считая от вершины S. Найдите объем пирамиды DABC.

106. От треугольной пирамиды, объем которой равен 12, отсечена треугольная пирамида плоскостью, проходящей через вершину пирамиды и среднюю линию основания. Найдите объем отсеченной треугольной пирамиды.

107. От призмы ABCA 1 B 1 C 1 , объем которой равен 6, отсечена треугольная пирамида C 1 ABC. Найдите объем оставшейся части.

108. Площадь осевого сечения цилиндра равна 4. Найдите площадь боковой поверхности цилиндра, деленную на π.

109. Найдите объем цилиндра, площадь основания которого равен 1, а образующая равна 6 и наклонена к плоскости основания под углом 30.

Читайте также: Ремонт главного тормозного цилиндра митсубиси аутлендер

110. Конус описан около правильной четырехугольной пирамиды со стороной основания 4 и высотой 6. Найдите его объем, деленный на π.

111. Во сколько раз объем конуса, описанного около правильной четырехугольной пирамиды, больше объема конуса, вписанного в эту пирамиду?

112. В основании прямой призмы лежит квадрат со стороной 2. Боковые ребра равны 2/ π. Найдите объем цилиндра, описанного около этой призмы.

113. Найдите площадь боковой поверхности правильной треугольной призмы, вписанной в цилиндр, радиус основания которого равен 2√3, а высота равна 2.

114. Найдите площадь боковой поверхности правильной треугольной призмы, описанной около цилиндра, радиус основания которого равен √3, а высота равна 2.

115. Найдите площадь боковой поверхности правильной шестиугольной призмы, описанной около цилиндра, радиус основания которого равен √3, а высота равна 2.

116. Около куба с ребром √3 описан шар. Найдите объем этого шара, деленный на π.

117. Боковые ребра треугольной пирамиды взаимно перпендикулярны, каждое из них равно 3. Найдите объем пирамиды.

118. Основанием пирамиды служит прямоугольник, одна боковая грань перпендикулярна плоскости основания, а три другие боковые грани наклонены к плоскости основания под углом 60°. Высота пирамиды равна 6. Найдите объем пирамиды.

119. Найдите объем призмы, в основаниях которой лежат правильные шестиугольники со сторонами 2, а боковые ребра равны 2√3 и наклонены к плоскости основания под углом 30°.

120. Из единичного куба вырезана правильная четырехугольная призма со стороной основания 0,5 и боковым ребром 1. Найдите площадь поверхности оставшейся части куба.

121. В треугольной призме две боковые грани перпендикулярны. Их общее ребро равно 10 и отстоит от других боковых ребер на 6 и 8. Найдите площадь боковой поверхности этой призмы.

122. В правильной четырёхугольной призме ABCDA 1 B 1 C 1 D 1 известно, что BD₁ =2AD. Найдите угол между диагоналями DB₁ и CA₁. Ответ дайте в градусах.

123. В прямоугольном параллелепипеде ABCDA 1 B 1 C 1 D 1 ребро АВ=2, ребро AD= √5, ребро AA₁=2. Точка К – середина ребра BB₁. Найдите площадь сечения,проходящего через точки A₁, D₁ и K.

124. В прямоугольном параллелепипеде ABCDA 1 B 1 C 1 D 1 ребро АВ=8, ребро AD=6, ребро AA 1 =21. Найдите синус угла между прямыми CD и A 1 C 1 .

125. Найдите объем правильной треугольной пирамиды, стороны основания которой равны 1, а высота равна √3.

126. Одна из граней прямоугольного параллелепипеда – квадрат. Диагональ параллелепипеда равна √8 и образует с плоскостью этой грани угол 45°. Найдите объем параллелепипеда.