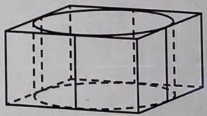
- Решение №2305 Цилиндр вписан в правильную четырёхугольную призму. Радиус основания и высота цилиндра равны 3.
- 11 класс. Геометрия. Тела вращения. Взаимные комбинации тел вращения.
- 11 класс. Геометрия. Тела вращения. Взаимные комбинации тел вращения.
- Вопросы
- Поделись с друзьями
- Комментарии преподавателя
- Цилиндр, вписанный в призму
- Условия, при которых цилиндр можно вписать в призму
- Задача №1
- Цилиндр, описанный около призмы
- Условия, при которых цилиндр можно описать около призмы
- Задача №2
- Разветвление: задача №3
- Заключение
- В правильную треугольную призму вписан цилиндр найти его площадь
- 📺 Видео
Видео:11 класс. Контрольная №4 (из 6). Тема: Объем призмы, цилиндра и конуса. Решение с советами! :)Скачать

Решение №2305 Цилиндр вписан в правильную четырёхугольную призму. Радиус основания и высота цилиндра равны 3.
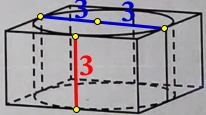
Цилиндр вписан в правильную четырёхугольную призму. Радиус основания и высота цилиндра равны 3. Найдите площадь боковой поверхности призмы.
Источник: Ященко ЕГЭ 2022 (36 вар)
Правильной четырёхугольной призмой – называется шестигранник, в основаниях которого находятся 2 квадрата, а боковые грани представлены прямоугольниками.
Площадь боковой поверхности данной призмы – это площадь 4-х равных прямоугольников.
Длина прямоугольника равна диаметру цилиндра, ширина прямоугольника равна высоте цилиндра.
Найдём площадь боковой поверхности призмы:
Sбок. поверх. = 4·Sпрямоугольника = 4· h ·( r + r ) = 4·3·(3 + 3) = 4·3·6 = 72
Видео:11 класс. Геометрия. Объем цилиндра. 14.04.2020Скачать

11 класс. Геометрия. Тела вращения. Взаимные комбинации тел вращения.
11 класс. Геометрия. Тела вращения. Взаимные комбинации тел вращения.
Вопросы
Задай свой вопрос по этому материалу!
Поделись с друзьями
Комментарии преподавателя
Видео:Цилиндр вписан в правильную четырехугольную призмуСкачать

Цилиндр, вписанный в призму
Говорят, что цилиндр вписан в призму (или призма описана около цилиндра), если основания цилиндра вписаны в соответствующие основания призмы (рис. 1). Очевидно, что их высоты совпадут (рис. 2).
Рис. 1. Цилиндр, вписанный в призму
Рис. 2. Цилиндр, вписанный в призму
Видео:GeoGebra: цилиндр, вписанный в правильную призмуСкачать

Условия, при которых цилиндр можно вписать в призму
Нужно, чтобы в основание призмы можно было вписать окружность. Что для треугольной и правильной призмы верно всегда (рис. 3, 4).
Читайте также: Размеры расточки блока цилиндров приора
Рис. 3. Цилиндр, вписанный в треугольную призму
Рис. 4. Цилиндр, вписанный в правильную шестиугольную призму
Вывод: цилиндр можно вписать в призму, если призма прямая, а в ее основание можно вписать окружность.
Для четырехугольный призмы необходимо чтобы призма была также прямой, а четырехугольник в основании был описанным. Т. е. суммы противоположных сторон были равны (рис. 5).
Рис. 5. Цилиндр, вписанный в четырехугольную призму
Видео:ЕГЭ 2017 по Математике. Призма вписана в цилиндр Задание 8 #4Скачать

Задача №1
Условие: в правильную треугольную призму, все ребра которой равны 6, вписан цилиндр. Найти его радиус и высоту (рис. 6).
Рис. 6. Иллюстрация к задаче 1
Заметим, что высота цилиндра равна высоте призмы, а значит, равна 6.
Радиус основания цилиндра равен радиусу окружности, вписанной в правильный треугольник со стороной 6. Радиус этой окружности находим по формуле 

Ответ: .
Видео:#130. Задание 8: комбинация телСкачать

Цилиндр, описанный около призмы
Говорят, что цилиндр можно описать около призмы (или призму вписать в цилиндр), если основания призмы вписаны в основания цилиндра. В данном случае, очевидно, снова будут равны высоты (боковые стороны призмы и образующие цилиндра) (рис. 7).
Рис. 7. Цилиндр, описанный около призмы
Видео:07 Стереометрия на ЕГЭ по математике. Призма вписана в цилиндр.Скачать

Условия, при которых цилиндр можно описать около призмы
Цилиндр можно описать около призмы, когда основание призмы можно вписать в окружность. Для треугольной -угольной правильной призмы – всегда, для четырехугольной – когда сумма противоположных углов в основании дает 180 градусов (рис. 8).
Рис. 8. Цилиндр, описанный около четырехугольной призмы
Видео:ЕГЭ. Профильная математика, задание 3Скачать

Задача №2
Условие: дана правильная шестиугольная призма, вписанная в цилиндр. Радиус основания цилиндра равен 7, а площадь боковой поверхности цилиндра равна 28. Найти площадь боковой поверхности призмы (рис. 9).
Рис. 9. Иллюстрация к задаче 2
Читайте также: Главный тормозной цилиндр мерседес виано
Сперва найдем высоту цилиндра. Так как 

Значит, и боковое ребро призмы также равно 2.
Далее, в основании призмы лежит правильный шестиугольник, вписанный в окружность. Как известно, сторона правильного шестиугольника равна радиусу описанной окружности, то есть 7.
Тогда площадь боковой поверхности призмы равна .
Видео:ЕГЭ. Задача 8. Призма и цилиндрСкачать

Разветвление: задача №3
Условие. Дана четырехугольная прямая призма, все ребра которой равны 1. Известно, что около этой призмы можно описать цилиндр. Найдите объем призмы и площадь полной поверхности данного цилиндра (рис. 10).
Рис. 10. Иллюстрация к задаче 3
Так как все ребра равны, то в основании призмы лежит ромб. Раз можно описать цилиндр около призмы, то ромб можно вписать в окружность, а значит, этот ромб – квадрат. Следовательно, призма – это куб со стороной 1, его объем также равен 1.
Высота цилиндра – 1, а радиус окружности равен половине диагонали квадрата, то есть 

Ответ: .
Видео:ВПИСАННАЯ И ОПИСАННАЯ ПРИЗМЫ // СТЕРЕОМЕТРИЯСкачать

Заключение
На уроке мы разобрали комбинации призмы и цилиндра, а также решили задачи по темам: цилиндр, описанный вокруг призмы и цилиндр, вписанный в призму.
Видео:#131. Задание 8: комбинация телСкачать

В правильную треугольную призму вписан цилиндр найти его площадь
Шар вписан в цилиндр. Площадь полной поверхности цилиндра равна 18. Найдите площадь поверхности шара.
Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 1. Найдите объем параллелепипеда.
Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 4. Объем параллелепипеда равен 16. Найдите высоту цилиндра.
В куб вписан шар радиуса 1. Найдите объем куба.
В основании прямой призмы лежит прямоугольный треугольник с катетами 6 и 8. Боковые ребра равны Найдите объем цилиндра, описанного около этой призмы.
В основании прямой призмы лежит квадрат со стороной 2. Боковые ребра равны Найдите объем цилиндра, описанного около этой призмы.
Читайте также: Замки под цилиндр для металлических дверей
Цилиндр и конус имеют общие основание и высоту. Объём конуса равен 25. Найдите объём цилиндра.
Из единичного куба вырезана правильная четырехугольная призма со стороной основания 0,5 и боковым ребром 1. Найдите площадь поверхности оставшейся части куба.
Цилиндр и конус имеют общие основание и высоту. Найдите объем конуса, если объем цилиндра равен 150.
Объём куба, описанного около сферы, равен 216. Найдите радиус сферы.
Конус описан около правильной четырехугольной пирамиды со стороной основания 4 и высотой 6. Найдите его объем, деленный на
Во сколько раз объем конуса, описанного около правильной четырехугольной пирамиды, больше объема конуса, вписанного в эту пирамиду?
В куб с ребром 3 вписан шар. Найдите объем этого шара, деленный на
Около куба с ребром описан шар. Найдите объем этого шара, деленный на
Вершина A куба с ребром 1,6 является центром сферы, проходящей через точку A1. Найдите площадь S части сферы, содержащейся внутри куба. В ответе запишите величину
📺 Видео
Видеоурок по математике "Цилиндр"Скачать

ЕГЭ 2022 математика задача 4 вариант 2Скачать

Призма и цилиндр. Практическая часть. 11 класс.Скачать

xi408 Комбинации с цилиндромСкачать

Шар вписан в треугольную призмуСкачать
Объемы прямой призмы и цилиндраСкачать

Стереометрия. В правильную четырехугольную призму вписан круглый цилиндра. Найдите высоту цилиндраСкачать

11 класс. Геометрия. Объем цилиндраСкачать

Задание 3. ЕГЭ математика 2024. Разбор за 42 минуты всех типов. Стереометрия ЕГЭ. Подготовка к ЕГЭ.Скачать