В правильную треугольную призму вписан цилиндр объем цилиндра равен (7 видео)

Содержание

Цилиндры, вписанные в призмы. Свойства призмы, описанной около цилиндра
Отношение объемов цилиндра и описанной около него правильной n — угольной призмы
Помогите пожалуйста
В правильную треугольную призму вписан цилиндр объем цилиндра равен
Как написать хороший ответ?
Решение №2305 Цилиндр вписан в правильную четырёхугольную призму. Радиус основания и высота цилиндра равны 3.
Задание 9
В правильную треугольную призму вписан цилиндр объем цилиндра равен
Решение
Ответ
Источники и прецеденты использования
🎦 Видео

Видео:Цилиндр вписан в правильную четырехугольную призмуСкачать

Цилиндры, вписанные в призмы. Свойства призмы, описанной около цилиндра

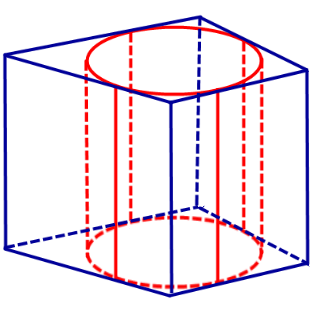
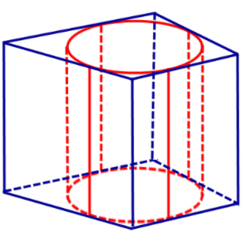
Определение 2. Если цилиндр вписан в призму, то призму называют описанной около цилиндра.

Прежде, чем перейти к вопросу о том, в какую же призму можно вписать цилиндр, докажем следующее свойство призм.

Утверждение 1. Если в основания призмы можно вписать окружности, то отрезок, соединяющий центры вписанных окружностей, будет параллелелен и равен боковому ребру призмы.

Рассуждая аналогичным образом, заключаем, что точка O’ равноудалена от всех прямых, на которых лежат ребра верхнего основания A’₁A’₂, A’₂A’₃, . , A_{n – 1}A_n , а поскольку O’ лежит в плоскости верхнего основания, то точка O’ является центром вписанной в многоугольник A’₁A’₂ . A’_n окружности.

В силу того, что прямые OO’ и A₁A’₁ параллельны по построению, а прямые OA₁ и O’A’ параллельны как линии пересечения двух параллельных плоскостей третьей плоскостью, замечаем, что четырехугольник OO’A₁A’₁ является параллелограммом, откуда вытекает равенство: OO’ = A₁A’₁ .

Теорема. В призму можно вписать цилиндр тогда и только тогда, когда выполнены следующие два условия:

Призма является прямой призмой;
В основания призмы можно вписать окружности.

Доказательство. Докажем сначала, что если в n – угольную призму вписан цилиндр, то оба условия теоремы выполнены.

Действительно, выполнение условия 2 следует непосредственно из определения цилиндра, вписанного в призму. Докажем, что выполняется и условие 1, т.е. докажем, что описанная около цилиндра призма является прямой призмой.

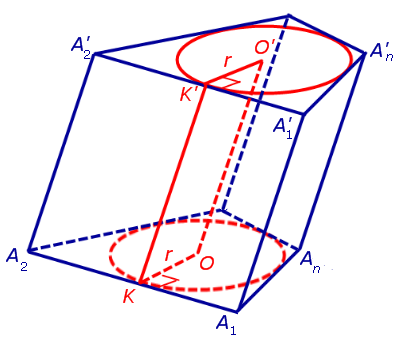
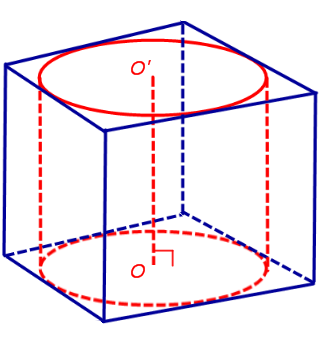
С этой целью рассмотрим ось цилиндра OO’ , соединяющую центры окружностей, вписанных в нижнее и верхнее основания призмы (рис. 3).

Согласно утверждению 1 отрезок OO’ параллелен боковым ребрам призмы. Поскольку ось цилиндра OO’ перпендикулярна к плоскостям его оснований, то и боковые ребра призмы также перпендикулярны к плоскостям оснований, то есть призма является прямой призмой.

Таким образом, мы доказали, что, если призма описана около цилиндра, то оба условия теоремы выполнены.

Теперь рассмотрим прямую n – угольную призму высоты h, в основания которой можно вписать окружности, и докажем, что в такую призму можно вписать цилиндр.

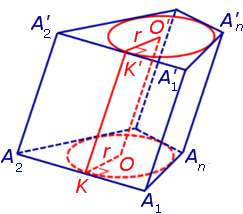
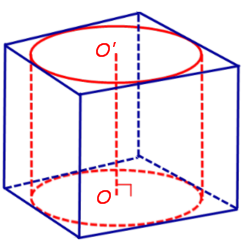
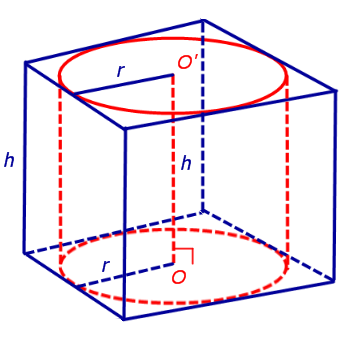
Обозначим буквой O центр окружности радиуса r, вписанной в нижнее основание призмы, а символом O’ обозначим центр окружности, вписанной в верхнее основание призмы (рис. 4).

Читайте также: Цилиндр гидроборта камаз сельхозник

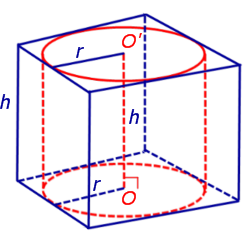
Поскольку многоугольники, лежащие в основаниях призмы равны, то и радиусы вписанных в них окружностей будут равны. Согласно утверждению 1 отрезок OO’ параллелен и равен боковому ребру призмы. Так как рассматриваемая призма прямая, то ее боковые ребра перпендикулярны плоскости основания и равны высоте призмы h. Значит, и отрезок OO’ перпендикулярен плоскости основания призмы и равен h.

Цилиндр с осью OO’ , радиусом r и высотой h и будет вписан в исходную призму.

Доказательство теоремы завершено.

Следствие 1 . Высота призмы, описанной около цилиндра, равна высоте цилиндра.

Следствие 2. В любую прямую треугольную призму можно вписать цилиндр.

Справедливость этого утверждения вытекает из того факта, что в любой треугольник можно вписать окружность.

Следствие 3. В любую правильную n – угольную призму можно вписать цилиндр.

Для доказательства этого следствия достаточно заметить, правильная призма является прямой призмой. Основаниями правильной призмы являются правильные многоугольники, а в любой правильный n – угольник можно вписать окружность.

Видео:ЕГЭ 2022 математика задача 4 вариант 2Скачать

Отношение объемов цилиндра и описанной около него правильной n — угольной призмы

Задача. Найти отношение объемов цилиндра и описанной около него правильной n — угольной призмы.

Решение. Поскольку и объем цилиндра, и объем призмы объем призмы вычисляются по формуле

а высота цилиндра равна высоте описанной около него призмы, то для объемов цилиндра и описанной около него правильной n — угольной призмы справедливо равенство

Следствие 4. Отношение объема цилиндра к объему описанной около него правильной треугольной призмы правильной треугольной призмы равно

Следствие 5. Отношение объема цилиндра к объему описанной около него правильной четырехугольной призмы правильной четырехугольной призмы равно

Следствие 6. Отношение объема цилиндра к объему описанной около него правильной шестиугольной призмы равно

Видео:#130. Задание 8: комбинация телСкачать

Помогите пожалуйста

В правильную треугольную призму вписан цилиндр,объем которого равен V Найтиобъем призмы

Образующая конуса наклонена к плоскости основания под углом альфа.Найти объем конуса если площадь его боковой поверхности S

Найти площадь сферы описанной около прямоугольного параллепипеда если его высота равна 4,а в основании лежит квадрат со стороной 8

Несоглашусь с предыдущими ответами.

1) Очевидно, в ответе должно участвовать П (=3,1415. )
Объёмы и цилиндра, и призмы равны произведению площади основания на высоту. Высота у них одинаковая. Следовательно отношение объёмов равно отношению площадей основания.
Основание призмы — правильный треугольник. Основание цилиндра — круг, вписанный в этот треугольник.
Радиус окружности, вписанной в правильный треугольник со стороной A равен sqrt(3)/6*A (sqrt — квадратный корень) .
Sкруга = П* (sqrt(3)/6*A)^2 = П/18 *A^2
Sтреугольника = 1/2*(sqrt(3)/2*A)*A= sqrt(3)/4*A^2
Sтреугольника = Sкруга*sqrt(3)/4/(П/18)=Sкруга*sqrt(3)*9/(2*П)
Vпризмы = sqrt(3)*9/(2*П) * Vцилиндра

2) Размерность не сходится. В ответе должна быть S^(3/2)
Пусть длина образующей конуса L, а радиус основания R. Пусть высота конуса H. Тогда площадь боковой поверхности: S=П*R*L
Рассмотрим сечение конуса плоскостью, проходящей через его ось. Имеем равнобедренный треугольник с боковой стороной L и основанием (2*R), при этом угол при основании равен A (альфа) .
L = R / cos(A).
H = R * tg(A)
Из площади: R= sqrt(S*cos(A)/П)
V=П/3*R^2*H = П/3*(S*cos(A)/П) ^(3/2) * tg(A) = sin(A)*sqrt(cos(A))/(3*sqrt(П)) *S^3/2

Читайте также: Тормозные цилиндры шевроле ланос 2007

3) По теореме Пифагора диагональ основания равна 8*sqrt(2) (=sqrt(8^2+8^2)).
По теореме Пифагора диагональ параллелепипеда = 12 = sqrt(144) = sqrt( (8*sqrt(2))^2 + 4^2)
Диагональ параллелепипеда это диаметр описанной сферы. Следовательно радиус равен 6.
Площадь сферы равна 4*П*r^2 = 144*П

Видео:11 класс, 32 урок, Объем цилиндраСкачать

В правильную треугольную призму вписан цилиндр объем цилиндра равен

В цилиндр вписана правильная треугольная призма Найдите. объем призмы, если обьем цилиндра равен 8 корней из 3х

Ответы и объяснения 1

Знаете ответ? Поделитесь им!

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
Писать без грамматических, орфографических и пунктуационных ошибок.

Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
Использовать мат — это неуважительно по отношению к пользователям;
Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Математика.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!

Математика — наука о структурах, порядке и отношениях, исторически сложившаяся на основе операций подсчёта, измерения и описания формы объектов.

Видео:11 класс. Контрольная №4 (из 6). Тема: Объем призмы, цилиндра и конуса. Решение с советами! :)Скачать

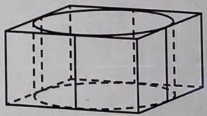
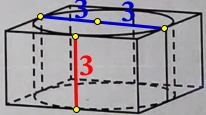
Решение №2305 Цилиндр вписан в правильную четырёхугольную призму. Радиус основания и высота цилиндра равны 3.

Цилиндр вписан в правильную четырёхугольную призму. Радиус основания и высота цилиндра равны 3. Найдите площадь боковой поверхности призмы.

Источник: Ященко ЕГЭ 2022 (36 вар)

Правильной четырёхугольной призмой – называется шестигранник, в основаниях которого находятся 2 квадрата, а боковые грани представлены прямоугольниками.
Площадь боковой поверхности данной призмы – это площадь 4-х равных прямоугольников.
Длина прямоугольника равна диаметру цилиндра, ширина прямоугольника равна высоте цилиндра.

Найдём площадь боковой поверхности призмы:

S_{бок. поверх.} = 4·S_{прямоугольника} = 4· h ·( r + r ) = 4·3·(3 + 3) = 4·3·6 = 72

Видео:11 класс. Геометрия. Объем цилиндра. 14.04.2020Скачать

Задание 9

Найдите объем правильной треугольной призмы, вписанной в цилиндр, радиус основания которого равен \(2\sqrt 3\) , а высота равна \(3\sqrt 3\) .

Объем призмы равен произведению площади основания на высоту \(V=S_oH.\) Высота известна из условия и равна \(3\sqrt 3\) . Осталось найти площадь основания.

Так как призма правильная, то в основании лежит правильный треугольник. Площадь правильного треугольника можно найти через радиус описанной окружности \(S_o= R^2.\)

Читайте также: Кашированные цилиндры что это такое

Тогда искомый объем равен \(V= (2\sqrt 3)^2*3\sqrt 3=81.\)

P.S. Можно не запоминать формулу площади правильного треугольника, так как здесь довольно просто можно вычислить длину стороны, зная радиус описанной окружности. Центр описанной окружности лежит в точке пересечения медиан. Медианы делятся точкой пересечения в отношении 2 к 1, считая от вершины. Из этих соображений находим длину медианы, а затем длину стороны и считаем площадь треугольника.

Пусть m — длина медианы (а в правильном треугольнике это высота и биссектрисса), тогда по определению синуса угла (а все углы в правильном треугольнике равны 60 градусам): \(sin60^o=m/a \Rightarrow a=m/sin60^o= m.\)

Так как медианы точкой пересечения делятся в отношении 2 к 1, считая от вершины, то \(R= m \Rightarrow m= R.\) Тогда \(a=\sqrt3R=6.\)

Площадь треуольника в основании равна \(S= a*a*sin60^o=9\sqrt 3\) , а тогда \(V=9\sqrt3*3\sqrt3=27*3=81.\)

Видео:Объём цилиндраСкачать

В правильную треугольную призму вписан цилиндр объем цилиндра равен

Правильная треугольная призма ABCA 1B 1C 1 описана около шара радиуса R . Точки M и N – середины рёбер BB 1 и CC 1 . В шар вписан цилиндр так, что его основание лежит в плоскости AMN . Найдите объём цилиндра.

Решение

Заметим, что высота призмы равна диаметру шара, т.е. 2R , шар касается плоскостей оснований призмы в центрах P и P 1 равносторонних треугольников ABC и A 1B 1C 1 , а плоскостей боковых граней – в точках пересечения их диагоналей. Пусть K и K 1 – середины BC и B 1C 1 соответственно. Ортогональная проекция шара на плоскость ABC есть круг радиуса R , вписанный в треугольник ABC . Поэтому
AP = A 1P 1 = R, PK = P 1K 1 = 2R, AK = A 1K 1 = 3R.
Рассмотрим сечение призмы плоскостью AKK 1A 1 . Получим прямоугольник AKK 1A 1 со сторонами 2R , 3R , круг радиуса R , касающийся сторон AK и A 1K 1 в точках P и P 1 , а стороны KK 1 – в её середине L , причём центр круга совпадает с центром O шара. Пусть LAK = α . Тогда
tg α = = = , cos α = .
Опустим перпендикуляр OQ из центра круга на прямую AL . Из прямоугольного треугольника OQL находим, что
QL = OL cos OLQ = R cos α = .
Пусть AQ пересекает окружность, ограничивающую круг, в точке E . Продолжим EO до пересечения с этой окружностью в точке F . Тогда EL – диаметр основания цилиндра, вписанного в данный шар, а LF – высота цилиндра. По теореме Пифагора из прямоугольного треугольника EFL находим, что
LF = = = .
Следовательно, объём цилиндра равен
π · QL 2 · LF = π( ) 2 · = .