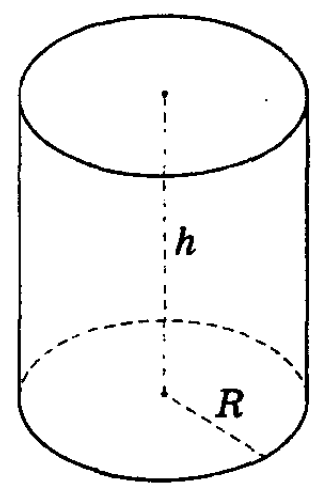
Тела вращения – это объемные тела, которые возникают при вращении некой плоской фигуры, которая ограничена кривой и крутится вокруг оси, лежащей в той же плоскости. К телам вращения относятся цилиндр, конус и шар.
Цилиндр — это объемное тело, которое получается при вращении прямоугольника вокруг одной из его сторон.
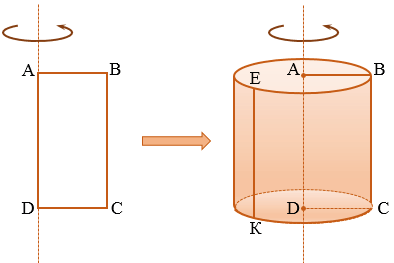
Возьмем прямоугольник АВСD. Будем вращать этот прямоугольник против часовой стрелки вокруг стороны АD.
Прямая АD — ось цилиндра.
Отрезок АD — высота цилиндра.
Основания цилиндра — два равных круга образованных при вращении сторон АВ и DC (круги равные, т.к. стороны АВ и DC равны как противоположные стороны прямоугольника).
Радиус цилиндра — радиус оснований цилиндра.
Цилиндрическая поверхность (или боковая поверхность цилиндра) — поверхность, образованная при вращении стороны ВС и состоящая из отрезков, параллельных оси цилиндра (АD).
Образующие цилиндра — отрезки, из которых составлена боковая поверхность цилиндра (на рисунке выше указаны образующие ВС и ЕК).
- Определение
- Объем цилиндра
- Доказательство:
- Площадь боковой поверхности цилиндра
- wiki.eduVdom.com
- Инструменты пользователя
- Инструменты сайта
- Боковая панель
- Цилиндр
- В развертке цилиндра что является основанием а что боковой поверхностью
- 5.4.1 Цилиндр. Основание, высота, боковая поверхность, образующая, развертка
- Тест по теме «Цилиндр» (11 класс) тест по геометрии (11 класс) на тему
- Скачать:
- Предварительный просмотр:
- 🔍 Видео
Определение
Объем цилиндра
Доказательство:
Дано: цилиндр с площадью основания S, высотой h и объемом V.
Доказать: V = Sh.
Доказательство:
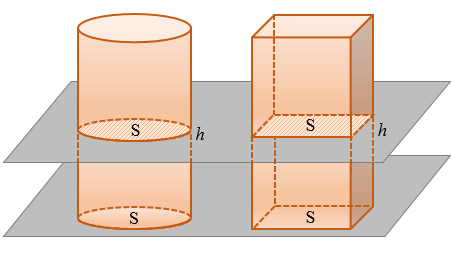
Воспользуемся принципом Кавальери. Рассмотрим цилиндр и призму с площадями оснований, равными S, и высотами, равными h, «стоящие» на одной плоскости.
Любая секущая плоскость, параллельная плоскости, на которой стоят цилиндр и призма, дает в качестве сечения цилиндра круг площади S, а в качестве сечения призмы — многоугольник площади S. Значит, объем цилиндра равен объему призмы. Но объем призмы равен Sh. Поэтому и объем цилиндра равен Sh, т.е. V = Sh. Что и требовалось доказать.
Площадь боковой поверхности цилиндра
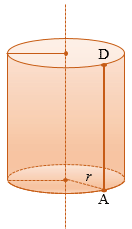
Рассмотрим цилиндр с радиусом r и высотой h.
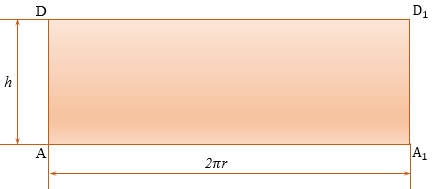
Представим, что его боковую поверхность разрезали по одной из его образующих АD и развернули так, что получился прямоугольник АDА1D1, стороны АD и А1D1 которого являются двумя краями разреза боковой поверхности цилиндра. Этот прямоугольник называется разверткой боковой поверхности цилиндра.
Сторона АА1 прямоугольника АDА1D1 равна длине окружности основания, а сторона АD равна высоте цилиндра, т.е. АА1 = 2 r, АВ = h. Площадь прямоугольника равна произведению его смежных сторон, значит, площадь прямоугольника АDА1D1 равна 2 rh.
Площадь Sбок боковой поверхности цилиндра равна площади ее развертки, т.е. Sбок = 2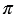 rh. rh. |
Поделись с друзьями в социальных сетях:
Видео:Видеоурок по математике "Цилиндр"Скачать

wiki.eduVdom.com
Инструменты пользователя
Инструменты сайта
Боковая панель
Стереометрия:
Видео:ПЛОЩАДЬ ПОЛНОЙ ПОВЕРХНОСТИ ЦИЛИНДРАСкачать

Цилиндр
Цилиндром ( прямым круговым цилиндром ) называется тело, состоящее из двух кругов ( оснований цилиндра ), совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие при параллельном переносе точки этих кругов. Отрезки, соединяющие соответствующие точки окружностей оснований, называются образующими цилиндра.
Читайте также: Задний тормозной цилиндр jetta 6
Цилиндр — тело, которое ограничено цилиндрической поверхностью с замкнутой направляющей и двумя параллельными плоскостями, пересекающими образующие данной поверхности.
Цилиндрическая поверхность — поверхность, которая образуется движением прямой линии вдоль некоторой кривой. Прямую называют образующей цилиндрической поверхности, а кривую линию — направляющей цилиндрической поверхности.
Боковая поверхность цилиндра — часть цилиндрической поверхности, которая ограничена параллельными плоскостями.
Основания цилиндра — части параллельных плоскостей, отсекаемые боковой поверхностью цилиндра.
Цилиндр называется прямым (См.Рис.1), если его образующие перпендикулярны плоскостям оснований. В противном случае цилиндр называется наклонным.
Круговой цилиндр — цилиндр, основания которого являются кругами.
Прямой круговой цилиндр ( просто цилиндр ) – это тело, полученное при вращении прямоугольника вокруг одной из его сторон. См.Рис.1.
Радиус цилиндра – радиус его основания.
Образующая цилиндра — образующая цилиндрической поверхности.
Высотой цилиндра называется расстояние между плоскостями оснований. Осью цилиндра называется прямая, проходящая через центры оснований. Сечение цилиндра плоскостью, проходящей через ось цилиндра, называется осевым сечением.
Ось цилиндра параллельна его образующей и является осью симметрии цилиндра.
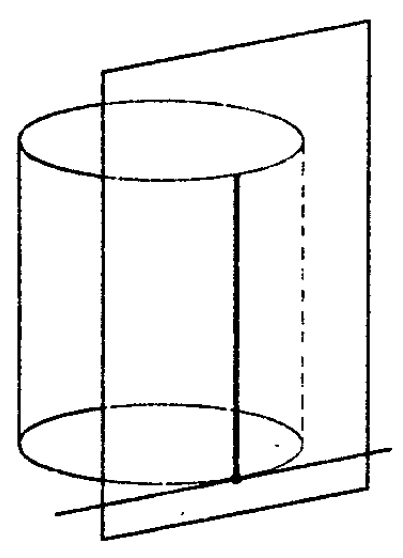
Плоскость, проходящая через образующую прямого цилиндра и перпендикулярная осевому сечению, проведенному через эту образующую, называется касательной плоскостью цилиндра. См.Рис.2.
Развёртка боковой поверхности цилиндра — прямоугольник со сторонами, равными высоте цилиндра и длине окружности основания.
Площадь боковой поверхности цилиндра — площадь развёртки боковой поверхности. $$S_ =2\pi\cdot rh$$ , где h – высота цилиндра, а r – радиус основания.
Площадь полной поверхности цилиндра — площадь, которая равна сумме площадей двух оснований цилиндра и его боковой поверхности, т.е. выражается формулой: $$S_ =2\pi\cdot r^2 + 2\pi\cdot rh = 2\pi\cdot r(r+h)$$ , где h – высота цилиндра, а r – радиус основания.
Объем всякого цилиндра равен произведению площади основания на высоту: $$V = S\cdot h$$ Объем круглого цилиндра: $$V=\pi r^2 \cdot h$$ , где (r — радиус основания).
Призма есть частный вид цилиндра (образующие параллельны боковым ребрам; направляющая — многоугольник, лежащий в основании). С другой стороны, произвольный цилиндр можно рассматривать как выродившуюся («сглаженную») призму с очень большим числом очень узких граней. Практически цилиндр неотличим от такой призмы. Все свойства призмы сохраняются и в цилиндре.
Видео:Тема 4. Цилиндр. Осевое сечение цилиндра. Развертка боковой поверхности цилиндра. Площадь боковойСкачать

В развертке цилиндра что является основанием а что боковой поверхностью
Ц илиндр, получается в результате вращения прямоугольника вокруг одной из его сторон.
- Цилиндр состоит из двух кругов и множества отрезков .
- Цилиндр – это геометрическое тело, состоящее из двух равных кругов, расположенных в параллельных плоскостях и множества отрезков, соединяющих соответственные точки этих кругов.
- Определения элементов цилиндра :
Основания цилиндра – равные круги, расположенные в параллельных плоскостях
Высота цилиндра — это расстояние между плоскостями его оснований.
Ось цилиндра – это прямая, проходящая через центры основания цилиндра (ось цилиндра является осью вращения цилиндра).
Осевое сечение цилиндра – сечение цилиндра плоскостью, проходящей через ось цилиндра (осевое сечение цилиндра является плоскостью симметрии цилиндра). Все осевые сечения цилиндра – равные прямоугольники
Читайте также: Ситроен с4 пропуск зажигания в первом цилиндре
Образующая цилиндра — это отрезок соединяющий точку окружности верхнего основания с соответственной точкой окружности нижнего основания. Все образующие параллельны оси вращения и имеют одинаковую длину, равную высоте цилиндра.
Образующая цилиндра при вращении вокруг оси образует боковую (цилиндрическую) поверхность цилиндра .
Радиус цилиндра – это радиус его основания.
Прямой цилиндр – это цилиндр, образующие которого перпендикулярны основанию.
Равновеликий цилиндр – цилиндр, у которого высота равна диаметру (показать равновеликий цилиндр: кнопкой со значком руки перевести модель обратно в интерактивный режим и изменить значение высоты и радиуса у предложенной модели так, чтобы ).
- Вывод формулы площади боковой поверхности.
Разверткой боковой поверхности цилиндра является прямоугольник со сторонами H и C , где H – высота цилиндра, а C – длина окружности основания. Получим формулы для вычисления площадей боковой S б и полной S п поверхностей: S б = H · C = 2π RH , S п = S б + 2 S = 2π R ( R + H ).
Задача № 1. Вычислить площадь боковой и полной поверхности цилиндра, у которого радиус равен 3 см, а высота 5 см (число пи и ответ округлить до целых).
2. Высота цилиндра равна h , радиус основания R . Найти площадь сечения плоскостью, проведенной параллельно оси цилиндра на, расстоянии a от нее.
Домашнее задание: 522, 524, 526.
Р.S/ кому интересно попрбуйте пройти по ссылке и посмотреть электронный ресурс про цилиндр
для начала на странице установите у себя на ПК модуль ОМS и закачайте модуль. На выскочившей таблице кликните воспроизвести. А дальше по порядку просмотрите все странички.
ВСЕМ СПАСИБО.
Видео:Цилиндр, конус, шар, 6 классСкачать

5.4.1 Цилиндр. Основание, высота, боковая поверхность, образующая, развертка
Видеоурок: Цилиндр. Решение задач
Лекция: Цилиндр. Основание, высота, боковая поверхность, образующая, развертка
Цилиндр
Давайте представим, известную нам, окружность, у которой есть центр в точке О. А теперь из каждой точки этой окружности проведем прямые, перпендикулярные данной окружности. Вся поверхность, которую образуют данные прямые – это и есть цилиндрическая плоскость.
Как еще можно получить цилиндр? Попробуйте взять лист бумаги, закрепить его вертикально и начать быстро вращать вокруг его оси. В таком случае Вы заметите, что быстро вращающийся лист будет рисовать некое объемное тело, которое и называется цилиндром.
У цилиндра есть два основания (верхнее и нижнее) и оба они имеют форму окружности. Перпендикулярная к основаниям плоскость, называется боковой поверхностью цилиндра.
Возьмите лист бумаги и соедините его противоположные края – Вы как раз получите боковую поверхность цилиндра. А что будет, если этот лист снова развернуть? Он снова будет иметь форму прямоугольника. Это значит, что боковая поверхность цилиндра – это прямоугольная плоскость.
Площадь поверхности цилиндра
Как уже писалось ранее, цилиндр состоит из оснований и боковой поверхности. Это значит, что для нахождения всей площади нам нужно знать площадь боковой поверхности цилиндров и основания.
Читайте также: Пневматический цилиндр как работает
Так как в основаниях лежит окружность, найти площадь оснований можно по следующей формуле: S = 2πR 2 .
Для тех, кто хорошо выучил тему об окружностях, возразят, что в формуле не должно быть цифры «2», однако из-за того, что основания в виде окружности два, и они равны между собой, площадь достаточно умножить на «2».
А теперь перейдем к площади поверхности. Как говорилось ранее, боковая поверхность создана прямоугольником, поэтому достаточно умножить длину его на ширину. Ширина – это высота цилиндра, а длина – это длина окружности, поэтому площадь боковой поверхности: S = 2πRH.
А значит, общая площадь поверхности цилиндра:
Видео:Построение развертки цилиндра. Урок 37.(Часть2.ПРОЕКЦИОННОЕ ЧЕРЧЕНИЕ)Скачать
Тест по теме «Цилиндр» (11 класс)
тест по геометрии (11 класс) на тему
Тест по теме «Цилиндр» (11 класс)
Видео:11 класс, 15 урок, Площадь поверхности цилиндраСкачать

Скачать:
Как сдать ЕГЭ на 80+ баллов?
Репетиторы Учи.Дома помогут подготовиться к ЕГЭ. Приходите на бесплатный пробный урок, на котором репетиторы определят ваш уровень подготовки и составят индивидуальный план обучения.
Бесплатно, онлайн, 40 минут
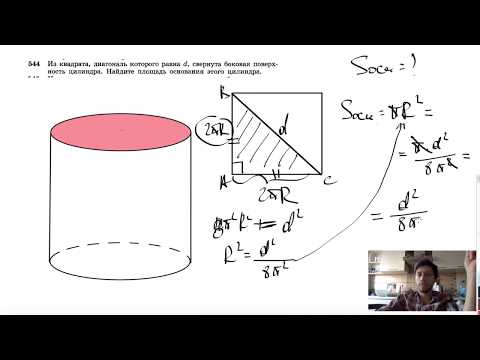
Видео:№544. Из квадрата, диагональ которого равна d, свернута боковая поверхность цилиндра.Скачать
Предварительный просмотр:
1. Цилиндр нельзя получить вращением…
1) треугольника вокруг одной из сторон;
2) квадрата вокруг одной из сторон;
3) прямоугольника вокруг одной из сторон.
2. Площадь боковой поверхности цилиндра можно вычислить по формуле…
3. Сечением цилиндра плоскостью, перпендикулярной его образующей, является …
1) круг; 2) прямоугольник; 3) трапеция.
4. На основаниях цилиндра взяты две параллельные друг другу хорды, проходящие через центры оснований. Тогда расстояние между хордами…
1) равно высоте цилиндра; 2) больше высоты цилиндра;
5. Боковой поверхностью цилиндра высотой H и диаметром основания d является квадрат. Тогда верно, что…
6. Развёрткой боковой поверхности прямого кругового цилиндра может быть…
1) прямоугольник; 2) ромб; 3) параллелограмм.
7. Отношение площадей боковой поверхности и осевого
сечения цилиндра равно…
8. Площадь боковой поверхности цилиндра в 2 раза больше площади основания. Тогда отношение равно…
1. Цилиндр можно получить вращением…
1) трапеции вокруг одного из оснований;
2) ромба вокруг одной из диагоналей;
3) прямоугольника вокруг одной из сторон.
2. Площадь боковой поверхности цилиндра нельзя вычислить по формуле…
3. Сечением цилиндра плоскостью, параллельной его образующей, является …
1) круг; 2) прямоугольник; 3) трапеция.
4. На основаниях цилиндра взяты две перпендикулярные друг другу хорды, проходящие через центры оснований.
Тогда расстояние между хордами…
1) равно образующей цилиндра; 2) больше высоты цилиндра;
3) меньше образующей цилиндра.
5. Боковой поверхностью цилиндра с высотой H и радиусом основания R является квадрат. Тогда верно , что…
6. Развёрткой боковой поверхности прямого кругового цилиндра не может быть…
1) прямоугольник; 2) ромб; 3) квадрат.
7. Площадь боковой поверхности цилиндра больше площади осевого сечения цилиндра в…
8. Площадь боковой поверхности цилиндра в 3 раза больше площади основания. Тогда отношение равно…
🔍 Видео
Геометрия. 11 класс. Цилиндр, его элементы. Развертка, площади боковой и полной поверхности цилиндраСкачать

60. Площадь поверхности цилиндраСкачать

ГЕОМЕТРИЯ 11 класс: Цилиндр. Площадь поверхностиСкачать

№558. Разверткой боковой поверхности конуса является сектор с дугой α. Найдите α, еслиСкачать
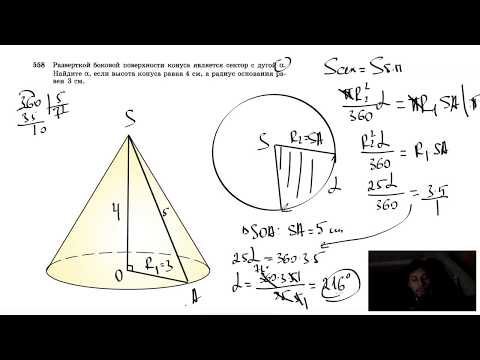
№561. Вычислите площадь основания и высоту конуса, если разверткой его боковой поверхностиСкачать
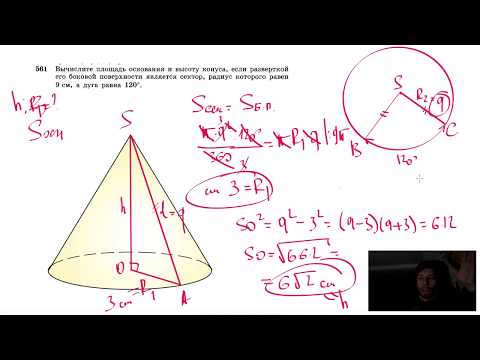
Нахождение площади боковой поверхности цилиндраСкачать

Лекция #13Скачать

Цилиндр и его элементыСкачать

№543. Угол между диагоналями развертки боковой поверхности цилиндра равен φ, диагональ равна d.Скачать

Развертка цилиндраСкачать

Цилиндр. Урок 17. Геометрия 9 классСкачать

Цилиндр. Конус.Скачать