В сферу вписан цилиндр образующая

Видео:Видеоурок по математике "Цилиндр"Скачать

Касательная прямая к сфере. Касательная плоскость к сфере

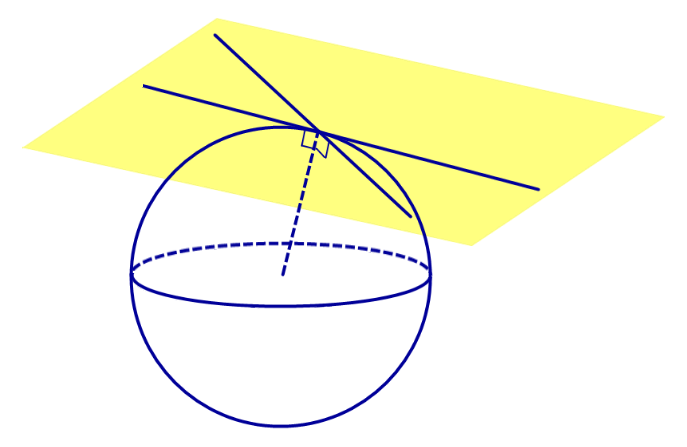
Определение 1. Прямую называют касательной к сфере (прямой, касающейся сферы), если эта прямая имеет со сферой единственную общую точку. Общую точку касательной прямой и сферы называют точкой касания (рис. 1).

Прямая касается сферы тогда и только тогда, когда эта прямая проходит через точку касания и перпендикулярна радиусу сферы, проведенному в точку касания.

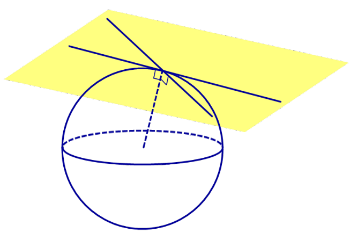
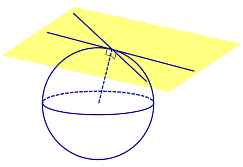
Множество всех прямых, касающихся сферы в некоторой точке, образуют касательную плоскость к сфере в этой точке (рис.2).

Плоскость касается сферы тогда и только тогда, когда плоскость и сфера имеют общую точку, причем только одну.

Плоскость касается сферы тогда и только тогда, когда плоскость и сфера имеют общую точку, причем плоскость перпендикулярна радиусу сферы, проведенному в эту точку.

Общую точку сферы и ее касательной плоскости называют точкой касания .

Видео:Линия пересечения двух поверхностей конус и цилиндр (Метод секущих плоскостей)Скачать

Сфера, вписанная в цилиндр

Определение 2. Сферой, вписанной в цилиндр, называют такую сферу, которая касается плоскостей обоих оснований цилиндра, а каждая образующая цилиндра является касательной к сфере (рис. 3).

Определение 3. Если сфера вписана в цилиндр, то цилиндр называют описанным около сферы .

Из рисунка 3 видно, что справедливы следующие два утверждения.

Утверждение 1. Около любой сферы можно описать цилиндр.

Утверждение 2. В цилиндр можно вписать сферу тогда и только тогда, когда высота цилиндра равна диаметру его основания.

Замечание. В том случае, когда в цилиндр можно вписать сферу, радиус вписанной сферы равняется радиусу основания цилиндра.

Видео:Цилиндр, конус, шар, 6 классСкачать

Отношение объемов шара и цилиндра, описанного около сферы, ограничивающей этот шар

Задача. Найти отношение объемов шара и цилиндра, описанного около сферы, ограничивающей этот шар.

Видео:Шар вписан в цилиндр. Площадь поверхности шара равна 78. Найдите площадь полной поверхности цилиндраСкачать

Сфера, описанная около цилиндра

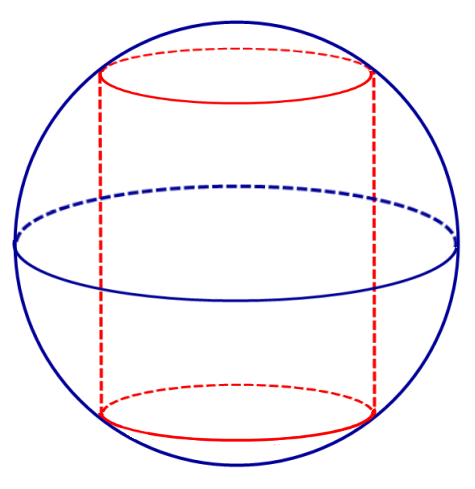
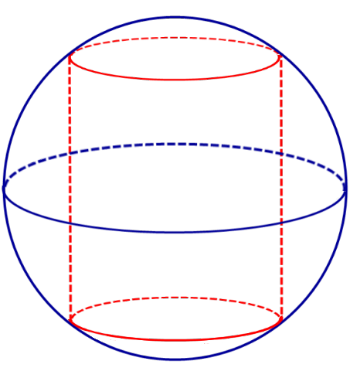
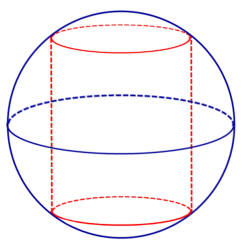
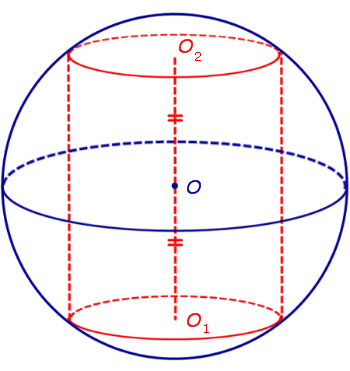
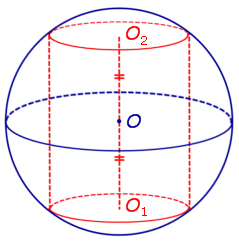
Определение 1. Цилиндром, вписанным в сферу, называют такой цилиндр, окружности оснований которого лежат на сфере (рис. 1).

Определение 2. Если цилиндр вписан в сферу, то сферу называют описанной около цилиндра.

Читайте также: Что зависит от количества цилиндров

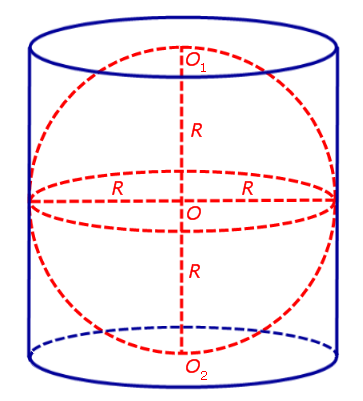
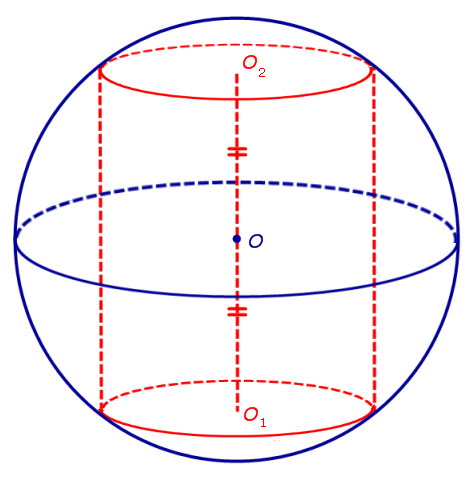
Утверждение. Около любого цилиндра можно описать сферу, причем только одну. Центр O этой сферы является серединой отрезка O₁O₂ , где O₁ и O₂ – центры оснований цилиндра (рис. 2)

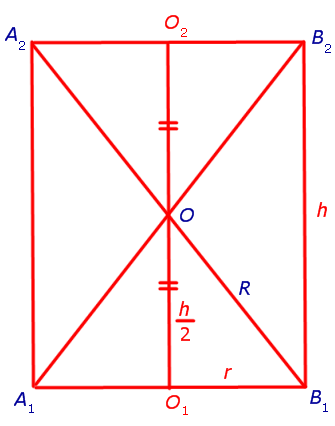
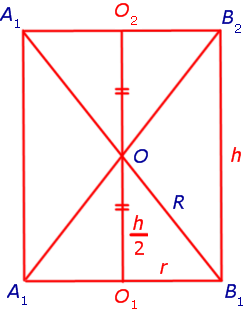
Доказательство. Обозначим буквами r и h радиус и высоту цилиндра и рассмотрим любое осевое сечение цилиндра (рис. 3).

Отрезки A₁A₂ и B₁B₂ , изображенные на рисунке 3, являются образующими цилиндра. Радиус R описанной сферы можно найти с помощью теоремы Пифагора из прямоугольного треугольника OB₁O₁ по формуле

Следствие 1. Радиус сферы, описанной около цилиндра с радиусом r и высотой h равен

Следствие 2. Отношение объема цилиндра к объему описанной около него сферы можно найти по формуле

Видео:Начертательная геометрия. Лекция 16. Часть 1.Скачать

Сфера, вписанная в цилиндр

Ищем педагогов в команду «Инфоурок»

Описание презентации по отдельным слайдам:

Описание слайда:

Сфера, вписанная в цилиндр
Сфера называется вписанной в цилиндр, если она касается его оснований и боковой поверхности (касается каждой образующей). При этом цилиндр называется описанным около сферы.
В цилиндр можно вписать сферу, если высота цилиндра равна
диаметру его основания.
Ее центром будет точка O, являющаяся
серединой отрезка, соединяющего центры оснований O1 и O2 цилиндра.
Радиус сферы R будет равен
радиусу окружности основания цилиндра.

Описание слайда:

Упражнение 1
В цилиндр высоты 2 вписана сфера. Найдите ее радиус.
Ответ: 1.

Описание слайда:

Упражнение 2
В цилиндр вписана сфера радиуса 1. Найдите высоту цилиндра.
Ответ: 2.

Описание слайда:

Упражнение 3
Радиус основания цилиндра равен 2. Какой должна быть высота цилиндра, чтобы в него можно было вписать сферу?
Ответ: 4.

Описание слайда:

Упражнение 4
Высота цилиндра равна 2. Каким должен быть радиус основания цилиндра, чтобы в него можно было вписать сферу?
Ответ: 1.

Описание слайда:

Упражнение 5
Осевым сечением цилиндра является прямоугольник со сторонами 1 и 2. Можно ли в этот цилиндр вписать сферу?
Ответ: Нет.

Описание слайда:

Упражнение 6
Осевым сечением цилиндра является квадрат. Можно ли в этот цилиндр вписать сферу?
Ответ: Да.

Описание слайда:

Упражнение 7
Можно ли вписать сферу в цилиндр, осевым сечением которого является ромб?
Ответ: Нет.

Описание слайда:

Упражнение 8
Можно ли вписать сферу в наклонный цилиндр?
Ответ: Нет.

Описание слайда:

Упражнение 9
Площадь осевого сечения цилиндра, в который вписана сфера, равна 4 см2. Найдите диаметр сферы.
Ответ: 2 см.

Описание слайда:

Упражнение 10
Периметр осевого сечения цилиндра, в который вписана сфера, равен 8 см. Найдите радиус сферы.
Ответ: 1 см.

Описание слайда:

Упражнение 11
Какой наибольший радиус может быть у сферы, помещающейся в цилиндр, радиус основания которого равен 2, и высота 1.
Ответ: 0,5 см.

Описание слайда:

Упражнение 12
Можно ли сферу радиуса 1 поместить в наклонный цилиндр, радиус основания которого равен 1, а боковое ребро равно 2 и наклонено к плоскости основания под углом 60о.
Ответ: Нет.

Описание слайда:

Упражнение 13
Какой наибольший радиус может быть у сферы, помещающейся в наклонный цилиндр, радиус основания которого равен 1, а боковое ребро равно 2 и наклонено к плоскости основания под углом 60о.
Ответ:

Читайте также: Цилиндр с поршнем под поршнем находится сжатый воздух

Описание слайда:

Сфера, описанная около цилиндра
Цилиндр называется вписанным в сферу, если окружности оснований цилиндра лежат на сфере. При этом сфера называется описанной около цилиндра.
Около любого цилиндра можно описать сферу. Ее центром будет точка O, являющаяся серединой отрезка, соединяющего центры оснований O1 и O2 цилиндра.
Радиус сферы R вычисляется по формуле

где h – высота цилиндра, r – радиус окружности основания.

Описание слайда:

Упражнение 1
Диагональ осевого сечения цилиндра равна 2. Найдите радиус сферы, описанной около этого цилиндра.
Ответ: 1.

Описание слайда:

Упражнение 2
Около цилиндра высоты 2 и радиуса основания 1 описана сфера. Найдите ее радиус.
Ответ:

Описание слайда:

Упражнение 3
Около цилиндра, радиус основания которого равен 1, описана сфера радиуса 2. Найдите высоту цилиндра.
Ответ:

Описание слайда:

Упражнение 4
Около цилиндра, высота которого равна 1, описана сфера радиуса 1. Найдите радиус основания цилиндра.
Ответ:

Описание слайда:

Упражнение 5
Найдите наименьший радиус сферы, в которую помещается наклонный цилиндр, радиус основания которого равен 1, образующая равна 2 и наклонена к плоскости основания под углом 60о.
Ответ:

Описание слайда:

Цилиндр, вписанный в призму
Цилиндр называется вписанным в призму, если его основания вписаны в основания цилиндра. При этом, призма называется описанной около цилиндра
В призму можно вписать цилиндр тогда и только тогда, когда
в ее основание можно вписать окружность.
Радиус основания цилиндра равен
радиусу окружности, вписанной в основание призмы.
Высота цилиндра равна
высоте призмы.

Описание слайда:

Упражнение 1
Можно ли вписать цилиндр в наклонную призму?
Ответ: Да, наклонный цилиндр.

Описание слайда:

Упражнение 2
В основании прямой призмы правильный треугольник со стороной 1. Найдите радиус окружности основания цилиндра, вписанного в эту призму.
Ответ:

Описание слайда:

Упражнение 3
В основании прямой призмы прямоугольный треугольник с катетами 6 и 8. Найдите радиус окружности основания цилиндра, вписанного в эту призму.
Ответ: 2.

Описание слайда:

Упражнение 4
Найдите радиус окружности основания цилиндра, вписанного в единичный куб.
Ответ:

Описание слайда:

Упражнение 5
В правильную шестиугольную призму, со стороной основания 1, вписан цилиндр. Найдите радиус окружности основания этого цилиндра.
Ответ:

Описание слайда:

Цилиндр, описанный около призмы
Цилиндр называется описанным около призмы, если его основания описаны около оснований цилиндра. При этом, призма называется вписанной в цилиндр
Около призмы можно описать цилиндр, если около ее оснований можно описать окружности.
Высота цилиндра равна
высоте призмы.
радиусу окружности, описанной около основания призмы.
Радиус основания цилиндра равен

Описание слайда:

Упражнение 1
Можно ли описать цилиндр около наклонной призмы?
Ответ: Да, наклонный цилиндр.

Описание слайда:

Упражнение 2
В основании прямой призмы правильный треугольник со стороной 1. Найдите радиус окружности основания цилиндра, описанного около этой призмы.
Ответ:

Описание слайда:

Упражнение 3
В основании прямой призмы прямоугольный треугольник с катетами 6 и 8. Найдите радиус окружности основания цилиндра, описанного около этой призмы.
Ответ: 5.

Читайте также: Пропуск зажигания в 1 цилиндре уаз патриот причина

Описание слайда:

Упражнение 4
В основании прямой призмы квадрат со стороной 1. Найдите радиус окружности основания цилиндра, описанного около этой призмы.
Ответ:

Описание слайда:

Упражнение 5
Около правильной шестиугольной призмы, со стороной основания 1, описан цилиндр. Найдите радиус окружности основания этого цилиндра.
Ответ: 1.

Описание слайда:

Упражнение 6
Около единичного тетраэдра описан цилиндр так, что вершины тетраэдра принадлежат окружностям оснований цилиндра. Найдите радиус основания и высоту цилиндра.
Ответ:

Описание слайда:

Упражнение 7
Около единичного октаэдра описан цилиндр так, что две противоположные вершины октаэдра находятся в центрах оснований цилиндра, а остальные вершины принадлежат боковой поверхности цилиндра. Найдите радиус основания и высоту цилиндра.
Ответ:

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Курс профессиональной переподготовки

Библиотечно-библиографические и информационные знания в педагогическом процессе

Курс повышения квалификации

Охрана труда

Курс профессиональной переподготовки

Охрана труда

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

также Вы можете выбрать тип материала:

Общая информация

Международная дистанционная олимпиада Осень 2021

Похожие материалы

Урок по математике «Геометрические фигуры. Признаки и характеристики предметов»

Сценарий открытого мероприятия, посвящённого 75-летию Победы в Великой Отечественной войне: «Памяти павших будьте достойны!»

Возможности и риски педагогической диагностики

Презентация на тему : «Этологическая теория»

Мастер-класс для воспитателей «Нетрадиционные техники лепки»

Презентация на тему: Электрический ток. Анализ опасности поражения током

«Вред и польза жевательной резинки»

Статья «Нетрадиционные формы обучения столяров»

Воспользуйтесь поиском по нашей базе из
5248172 материала.

Вам будут интересны эти курсы:

Оставьте свой комментарий

В школе в Пермском крае произошла стрельба

Студенты разработали программу для предупреждения опасного поведения в школах

Минпросвещения планирует прекратить прием в колледжи по 43 профессиям

Google сможет удалять снимки с детьми из результатов поиска по запросу

Минпросвещения намерено включить проверку иллюстраций в критерии экспертизы учебников

Школьников не планируют переводить на удаленку после каникул

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

🔍 Видео

Сфера и шар. Сечение сферы. Вписанная и описанная сфераСкачать

xi408 Комбинации с цилиндромСкачать

Начертательная геометрия (задача 4-5) Пересечение поверхностейСкачать

ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТЕЙ ЦИЛИНДРА И ШАРА (СФЕРЫ). Инженерная графика[crossing of cylinder & sphere]Скачать

Цилиндр, конус и шар в задании 2 | Математика ЕГЭ 2023 | УмскулСкачать

Урок 19. Задачи на тела вращения из ЕГЭ. Цилиндр, конус, сфера. Стереометрия с нуля.Скачать

11 класс, 25 урок, Сфера, вписанная в цилиндрическую поверхностьСкачать

ЦИЛИНДР. КОНУС. ШАР. ЕГЭ. ЗАДАНИЕ 5.СТЕРЕОМЕТРИЯСкачать

xi410 Комбинации со сферойСкачать

Геометрия 11 класс (Урок№9 - Взаимное расположение сферы и тел вращения.)Скачать

ЦИЛИНДР. КОНУС. ШАР.Скачать

Комбинации тел. Урок 20. Геометрия 11 классСкачать

Геометрия 11 класс (Урок№6 - Тела вращения. Цилиндр.)Скачать

Пересечение конуса и сферыСкачать

Задание №756 — ГДЗ по геометрии 11 класс (Атанасян Л.С.)Скачать