В трех проекциях геометрическое тело цилиндра (5 видео)

Присмотритесь к окружающим нас предметам. Многие из них имеют форму геометрических тел или их сочетаний.

Форма деталей, встречающихся в технике, также представляет собой сочетание различных геометрических тел или их частей. Например, ось (рис. 124, а) образована в результате добавления к одному цилиндру другого цилиндра, меньшего по размерам, а втулка (рис. 124, б) получилась после того, как из цилиндра удалили другой цилиндр меньшего диаметра.

Рис. 124. Деталь как суумма или разность геометрических тел

Форма каждого геометрического тела и его изображений на чертеже имеет свои характерные признаки. Этим пользуются, чтобы облегчить чтение и выполнение чертежей.

Деталь мысленно расчленяют на отдельные составляющие ее части, имеющие изображения, характерные для известных нам геометрических тел.

Мысленное расчленение предмета на составляющие его геометрические тела называется анализом геометрической формы.

Из каких геометрических тел состоит деталь, изображенная на рис. 125?

Рис. 125. Заготовка ключа

Форма детали состоит из усеченного конуса, цилиндра, куба, цилиндра, части шара (рис. 126, а). Из большего цилиндра удален элемент цилиндрической формы.

После такого анализа форму детали представить легче (рис. 126, б). Поэтому необходимо знать характерные особенности проекций геометрических тел.

Рис. 126. Анализ геометрической формы заготовки ключа: а — элементы детали; б — общий вид детали

Цилиндр и конус. Проекции цилиндра и конуса показаны на рис. 127, а и б. Круги, лежащие в основаниях цилиндра и конуса, расположены параллельно горизонтальной плоскости проекций; проекции оснований на горизонтальную плоскость будут также кругами.

Фронтальная и профильная проекция цилиндра — прямоугольники, а конуса — равнобедренные треугольники.

На рис. 127в, дан чертеж усеченного конуса, горизонтальная проекция которого представляет собой две окружности, а фронтальная проекция — равнобочную трапецию.

Выполнение чертежей цилиндра и конуса начинают с проведения осей симметрии.

Из рис. 127, а видно, что фронтальная и профильная проекции цилиндра одинаковы. То же можно сказать о проекциях конуса. Поэтому в данном случае профильные проекции на чертеже лишние. На рисунке они даны лишь для того, чтобы показать, какую форму имеют все три проекции цилиндра и конуса.

Размеры цилиндра и конуса определяются высотой h и диаметром основания d. Для усеченного конуса указывают высоту h и диаметры обоих оснований D и d.

Рис. 127. Цилиндр и конус: а, б и в — комплексные чертежи; построения изометрической проекции; г, д и е — последовательность

Знак диаметра ∅ позволяет определять форму предмета и по одной проекции (рис. 128).

Видео:Как начертить КОНУС С ВЫРЕЗОМ (чертеж + аксонометрия)Скачать

Рис. 128. Рациональное выполнение изображений цилиндра и конуса

Для построения изометрической проекции цилиндра и конуса (см. рис. 127, г и д) проводят оси х и у, на которых строят ромб со стороной, равной диаметру предмета, в ромб вписывают овал (построение овала см. рис. 96); вдоль оси z откладывают высоту предмета. Для цилиндра и усеченного конуса строят второй овал и проводят касательные к овалам.

Читайте также: Объем цилиндра с разными диаметрами

Куб и прямоугольный параллелепипед. При проецировании куб располагают так, чтобы его грани были параллельны плоскостям проекций. Тогда на параллельных плоскостях грани изобразятся в натуральную величину, т. е. квадратами, а на перпендикулярных плоскостях — прямыми линиями. Проекциями куба являются три равных квадрата (рис. 129, а).

Построение изометрической проекции куба показано на рис. 129, в.

Прямоугольный параллелепипед проецируется подобно кубу. На рис. 129, б приведены три его проекции — прямоугольники.

На чертеже куба и параллелепипеда проставляют три размера: длину, высоту и ширину.

Рис. 129. Куб и прямоугольный параллелепипед: а и б — комплексные чертежи; в — последовательность построения изометрической проекции

На рис. 130, а приведено наглядное изображение детали, а на рис. 130, б дан ее чертеж. Деталь состоит из двух прямоугольных параллелепипедов, имеющих по две квадратные грани. Обратите внимание, как проставлены на чертеже размеры.

Рис. 130. Рациональное выполнение чертежа

Применение условного знака □ позволило вычертить деталь в одной проекции. Тонкие пересекающиеся линии на чертеже означают, что отмеченные ими поверхности — плоские.

Правильные треугольная и шестиугольная призмы. Основания призм, параллельные горизонтальные плоскости проекций, изображаются на ней в натуральную величину, а на фронтальной и профильной плоскостях — в виде прямых линий. Боковые грани изображаются в натуральную величину на плоскостях проекций, которым они параллельны, и в виде линий на тех плоскостях, которым они перпендикулярны (рис. 131, а и б). Грани, наклонные к плоскостям проекций, изображаются искаженными.

Рис. 131. Правильные призмы: а и б — комплексные чертежи; в и г — последовательность построения изометрической проекции

Размеры призм определяются высотой и размерами фигуры основания. Штрихпунктирными линиями на чертежах проводят оси симметрии.

Построение изометрии призм (рис. 131, в и г) начинают с основания. Затем из каждой вершины основания восставляют перпендикуляры, откладывают на них высоту и проводят линии, параллельные ребрам основания.

Выполнение чертежей начинают также с горизонтальной проекции.

Правильная четырехугольная пирамида. Квадратное основание пирамиды проецируется на горизонтальную плоскость в натуральную величину. На проекции основания пирамиды диагоналями изображаются боковые ребра, идущие от вершин основания к вершине пирамиды (рис. 132, а). Фронтальная и профильная проекции пирамиды — равнобедренные треугольники.

Размеры пирамиды определяются длиной b двух сторон основания и высотой h.

Построение изометрической проекции пирамиды (рис. 132, б) начинают с основания. Затем из центра полученной фигуры восставляют перпендикуляр, откладывают на нем высоту и соединяют полученную точку с вершинами основания.

Рис. 132. Правильная пирамида: а — комплексный чертеж; б — последовательность построения изометрической проекции

Шар. Все проекции шара (рис. 133) — круги, диаметр которых равен диаметру шара. На каждой проекции проводят центровые линии.

Читайте также: Квадрат в цилиндре как доказать что это квадрат

Видео:Как начертить цилиндр в объемеСкачать

Рис. 133. Комплексный чертеж шара

Тор. На рис. 134, а даны две проекции тора (кругового кольца). На фронтальной проекции в натуральную величину изображается окружность, в результате вращения которой образуется тор. Горизонтальная проекция представляет собой две концентрические окружности. Радиус внешней окружности больше радиуса внутренней на величину, равную диаметру образующей окружности.

Рис. 134. Тор: а — две проекции; б — деталь, имеющая торовые поверхноти

Размеры тора определяются диаметром (или радиусом) образующей окружности и внутренним (или наружным) диаметром кольца. На всех проекциях проводят оси симметрии. Среди поверхностей детали, изображенной на рис. 134, б, есть две торовые поверхности. Радиус образующей окружности одного тора 16 мм, другого — 12 мм.

Ответьте на вопросы

1. В чем заключается анализ геометрической формы предметов? Каково его значение?

2. Что общего и в чем отличие между проекциями цилиндра и конуса?

3. Какую форму имеют проекции куба и прямоугольного параллелепипеда?

4. Что означают тонкие пересекающиеся линии на проекции предмета ?

5. Какую форму имеют проекции правильной треугольной и шестиугольной призм, правильной четырехугольной пирамиды?

6. Сколькими и какими размерами определяется величина цилиндра, конуса, куба, параллелепипеда, правильных треугольной и шестиугольной призм, правильной четырехугольной пирамиды, шара, тора?

7. Для каких геометрических тел при наличии размеров можно ограничиться одной проекцией?

8. У каких геометрических тел все проекции одинаковы?

Задания к § 19

Упражнение 62

Запишите в рабочей тетради наименования и размеры геометрических тел, на которые можно расчленить формы деталей (рис. 135, а и б).

Форма записи:

Упражнение 63

Вычертите по три проекции и выполните технические рисунки следующих геометрических тел: цилиндра, конуса, правильных треугольной и шестиугольной призм и пирамиды. При выполнении чертежей не забудьте провести осевые и центровые линии. Правильно нанести размеры, следуя примерам, данным на рис. 127, а и б; 131, а и б; 135, а. Величину деталей определите обмериванием изображений на этих рисунках. Чертежи выполните в масштабе 5 : 1.

Упражнение 64

Видео:Проекции точек на поверхности цилиндра. Урок 36.(Часть2.ПРОЕКЦИОННОЕ ЧЕРЧЕНИЕ)Скачать

Пользуясь конструктором для моделирования А. Н. Сальникова, сложите указанные Вам преподавателем модели, привете денные на рис. 136, а — з. (Конструктор для моделирования A. H. Сальникова состоит из элементов, представляющих собой геометрические тела или их части. Он входит в комплект оборудования кабинета черчения.) При отсутствии конструктора изготовьте модели из дерева, пенопласта или другого материала.

Рис. 136. Задания на моделирование

Упражнение 65

Рассмотрите чертежи, приведенные на рис. 137, а — в, и ответьте на следующие вопросы применительно к каждому чертежу:

Рис. 137. Задания для упражнений

1. Какие виды даны на чертеже?

2. Из каких геометрических тел состоит деталь?

3. Каковы размеры каждого геометрического тела?

4. Какова шероховатость поверхностей детали? Выполните чертежи геометрических тел, на которые можно расчленить деталь, и технический рисунок детали.

Читайте также: Как выглядят цилиндры внутри

Упражнение 66

Начертите деталь по описанию, приведенному ниже, и нанесите на чертеж размеры.

Деталь имеет форму цилиндра диаметром 35 мм. В центре одного горца просверлено глухое отверстие диаметром 20 и длиной 30 мм. Другой конец детали — квадратная призма. Размеры основания призмы 24 х 24 мм, высота ее 30 мм. Общая длина детали 90 мм. Шероховатость всех поверхностей соответствует Rz 25.

Упражнение 67

Чертежи деталей на рис. 138 содержат один, два или три вида. Запишите в рабочей тетради, какие чертежи выполнены наиболее рационально, и объясните почему.

Форма записи:

Рис. 138. Задания на определение рациональности чертежа

Построение вырезов на геометрических телах

Видео:1.4 ЦИЛИНДР. Геометрические тела.Скачать

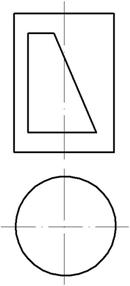
Пример 1. Построить три проекции цилиндра с вырезом (рис. 147).

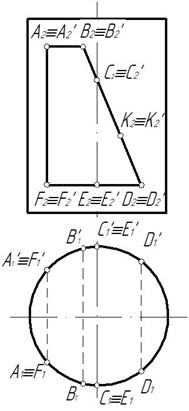
Отмечаем характерные точки выреза А, В, С, Д, Е, F, а также произвольную точку к для построения профильной проекции части эллипса. Горизонтальные проекции точек отмечаем на горизонтальном очерке цилиндра, так как горизонтальная проекция боковой поверхности цилиндра совпадает с горизонтальным очерком (рис .148)

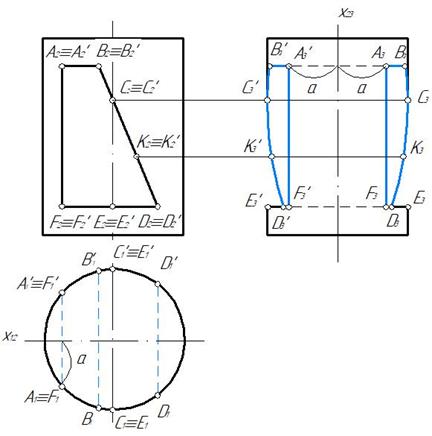
Построение профильной проекции выреза показано на рис. 149. Для этого целесообразно ось x ₁₂ провести через ось симметрии горизонтальной проекции,а ось x ₂₃ через профильную ось симметрии.

Пример 2. Построить три проекции конуса с вырезом (рис. 150).

Отмечаем характерные точки вареза А, В, С, Е, K, а также произвольную точку D для построения части эллипса. Горизонтальные проекции точек отмечаем на образующих конуса и вспомогательных окружностях (рис. 151).

На рис. 152 показано построение профильной проекции конуса с вырезом.Для этого целесообразно ось x ₁₂ провести через ось симметрии горизонтальной проекции, а ось x ₂₃ через профильную ось симметрии.

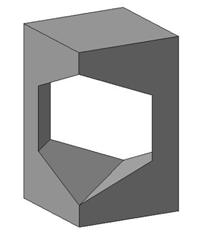
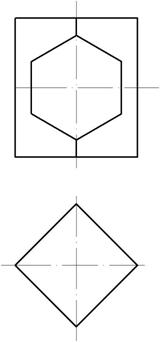
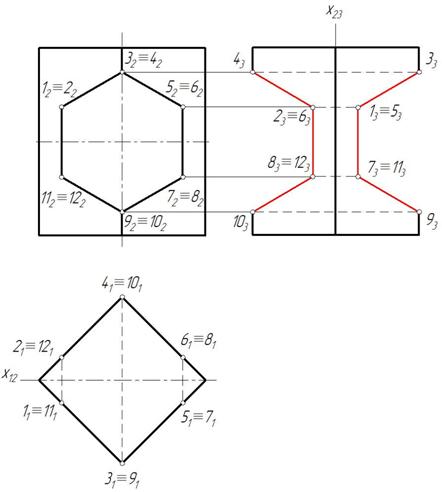
Пример 3. Построить три проекции вырезе на призме (рис. 153).

Решение показано на рис. 154

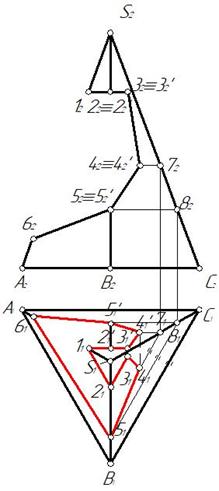
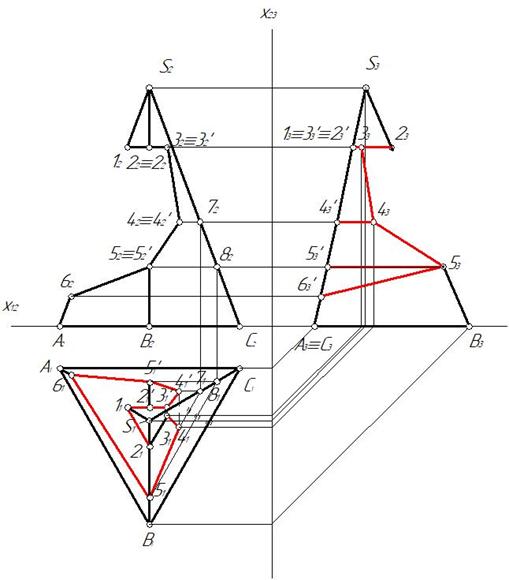
Пример 4. Построить три проекции выреза на пирамиде (рис. 155).

Отмечаем фронтальные проекции характерных точек выреза – это точки 1₂, 2₂, 3₂, 4₂, 5₂, 6₂. Для нахождения горизонтальных проекций точек 4 и 5 проводим по поверхности пирамиды две вспомогательные линии, параллельные основанию пирамиды ABC. Горизонтальные проекции этих линий являются треугольниками, параллельными горизонтальной проекции основания А₁В₁С₁. На этих треугольниках отмечаем горизонтальные проекции точек 4 и 5 (рис. 156).

Затем строим профильную проекцию пирамиды и точек выреза. Для этого оси целесообразно провести как показано на рис. 157.

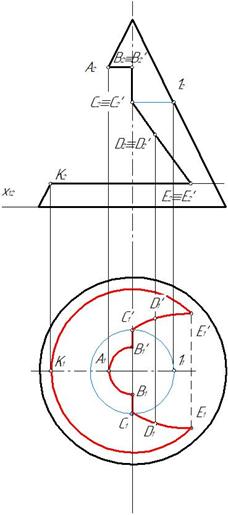
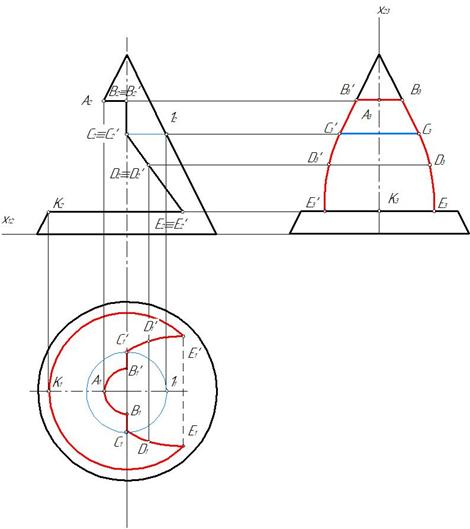
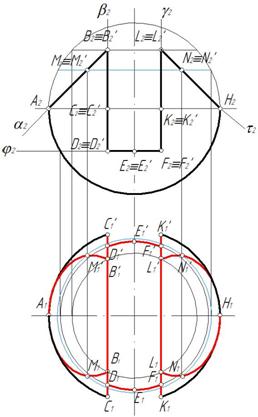
Пример 5. Построить три проекции выреза на сфере (рис. 158).

Вырез образован двумя фронтально-проецирующими плоскостями α и τ, горизонтальной плоскостью φ, двумя профильными плоскостями β и γ. Горизонтальная плоскость пересекает поверхность сферы по части окружности, ограниченной прямой. Фронтально-проецирующая плоскость пересекают поверхность сферы по окрухностям, которые на горизонтальной и профильной плоскости проецируются как части эллипсов. Профильная плоскость пересечет поверхность сферы по части окружности, которая на профильной плоскости спроецируется как часть окружности (рис. 159).