В цилиндр можно вписать сферу если (7 видео)

@ Часто встречаются и представляют интерес задачи, в которых взаимодействуют тела вращения с телами вращения и многогранниками.

Сфера называется описанной около цилиндра (конуса), если окружности его оснований (окружность его основания и вершина) принадлежат сфере.

Около любого цилиндра и любого конуса можно описать сферу.

Сфера называется вписанной в цилиндр , если она касается каждой образующей и обоих оснований цилиндра.

В цилиндр можно вписать сферу тогда и только тогда, когда его высота равна диаметру основания.

Центр сферы является серединой отрезка, соединяющего центры оснований.

Сфера называется вписанной в конус , если она касается образующих конуса и его основания.

В любой конус можно вписать сферу.

Сфера называется вписанной в усеченный конус , если она касается всех образующих и обоих оснований конуса.

Очевидно справедливо утверждение: в усеченный конус можно вписать сферу тогда и только тогда, когда образующая усеченного конуса равна сумме радиусов оснований. Тогда диаметр сферы равен высоте усеченного конуса.

Понятия вписанная и описанная сферы и вписанный и описанный шары в задачах не различаются.

Цилиндр называется вписанным в конус , если одно его основание принадлежит основанию конуса, а второе совпадает с сечением конуса плоскостью, параллельной основанию.

Основание цилиндра и основание конуса – концентрические круги.

Во всякий конус можно вписать цилиндр. Его высота меньше высоты конуса.

Цилиндр называется вписанным в усеченный конус , если одно его основание принадлежит основанию конуса, а другое совпадает со вторым основанием конуса. Высота такого цилиндра равна высоте усеченного конуса.

Так как цилиндр и конус однозначно определяются двумя независимыми параметрами, то, задав два независимых параметра одной фигуры и один параметр другой (вписанной или описанной), можно найти остальные параметры.

1 . В конус высоты Н и радиуса R вписан цилиндр высоты h . Найти радиус основания цилиндра.

Шар задается однозначно одним параметром, поэтому, задав параметр шара и один из независимых параметров вписанного или описанного конуса или цилиндра, можно найти другой параметр.

Или же по двум независимым параметрам конуса или цилиндра можно определить параметр вписанного или описанного шара.

2. В конус высоты Н и радиуса R вписан шар. Найти радиус шара.

3. В усеченный конус, радиусы оснований которого R и r , вписан шар. Найти его радиус.

4. В шар радиуса R вписан цилиндр высоты Н . Найти радиус его основания.

Пример 7.6.2. (КубГУ, матем., 1971 г.)

В прямой конус с образующей 1 и углом 2 a при вершине осевого сечения вписан шар. Вычислить радиус окружности, по которой соприкасаются поверхности конуса и шара, а также объем и полную поверхность меньшей из частей шара, на которые он рассекается кругом упомянутого радиуса. Решение

Решение задач о вписанных телах вращения, как правило, сводится к планиметрическим. Поэтому сделаем чертеж осевого сечения конуса. Тогда сфера будет окружностью большого круга, вписанной в равнобедренный треугольник. Отрезок прямой, параллельной основанию, соединяющий точки касания окружности и треугольника, будет диаметром искомой окружности.

Из прямоугольного треугольника ACD имеем AD = 1 sin a .

АО – биссектриса угла CAD , следовательно, .

Из прямоугольного треугольника AOD находим , OD = OM как радиусы.

D MKO подобен D CMO , следовательно, KMO = a

Меньшая часть шара – шаровой сегмент, высота которого РК . Его объем и площадь поверхности вычисляются по формулам

Тогда PK = PO — OK . Подставив найденные величины и преобразовав, получим ,

Пример 7.6.3. (КубГУ, матем., 1979 г.)

Пример 7.6.4. (КубГУ, матем., 1986 г.)

В усеченный конус вписан шар, касающийся обоих оснований и боковой поверхности. Найти длину образующей усеченного конуса, если даны его высота h и радиус a окружности касания. Решение

Сделаем чертеж осевого сечения. Тогда MK = a , BP = h . Так как высота конуса равна диаметру шара, то . Р OMK = Р ABP , как острые углы со взаимно перпендикулярными сторонами. Тогда D OMK подобен D ABP и имеет место соотношение , откуда .

Ответ: .

Пример 7.6.5. (КубГУ, эконом., 1989 г.)

Пусть AC = a , тогда из чертежа осевого сечения находим CD = a tg a , .

Разделив обе части на , получим .

Из прямоугольного треугольника имеем , тогда

Пример 7.6.6. (КубГУ, матем., 1979 г.)

В усеченный конус вписан шар радиуса R . Образующая конуса наклонена к плоскости нижнего основания под углом ( a 90°) . Найти объем усеченного конуса. Решение

В шар радиуса R вписан конус. Угол между образующей конуса и плоскостью основания равен a . В конус вписан шар. Найти радиус вписанного шара. Решение

В осевом сечении конуса получили равнобедренный треугольник с вписанной и описанной окружностями. Отметим, что центры вписанной и описанной окружностей совпадают только у правильного треугольника. Если угол при вершине равнобедренного треугольника меньше 60° , то центр описанной окружности расположен на высоте ближе к этой вершине, чем центр вписанной окружности. Если треугольник прямоугольный, то центр описанной окружности совпадает с серединой гипотенузы, если же треугольник тупоугольный, то центр описанной окружности будет расположен вне треугольника, в то время как центр вписанной окружности для любого треугольника является внутренней точкой.

Если О – центр вписанной окружности, то АО биссектриса D CAD и из треугольника OAD находим .

Пример 7.6.8. (КубГУ, физич., 1979 г.)

Шар радиуса R вписан в конус. Из центра шара образующая конуса видна под углом a . Найти объем конуса. Решение

Пусть О – центр вписанной окружности в осевом сечении конуса. По условию Р AOC = a , тогда Р AOD = 180° — a . Очевидно, что a > 90° . Из прямоугольного треугольника AOD находим Р OAD = 180° — (90° + 180° -a) = a — 90° . АО – биссектриса Р CAD . Следовательно, Р CAD = 2 Р OAD = 2 a — 180° .
OD =R . Тогда из треугольника AOD находим AD. AD = OD tg AOD = R tg( 180° -a ) = — R tg a .

Из треугольника AСD находим СD

Подставив найденные величины в формулу объема, получим

Если 90° a 135° , то 180° a 270° ; тогда tg a , tg 2 a >0 и .

Если 135° a 180° , то 270° a 360° ; тогда tg 2 a , tg 2 a и .

Содержание

Сфера, описанная около цилиндра
Сфера, вписанная в цилиндр
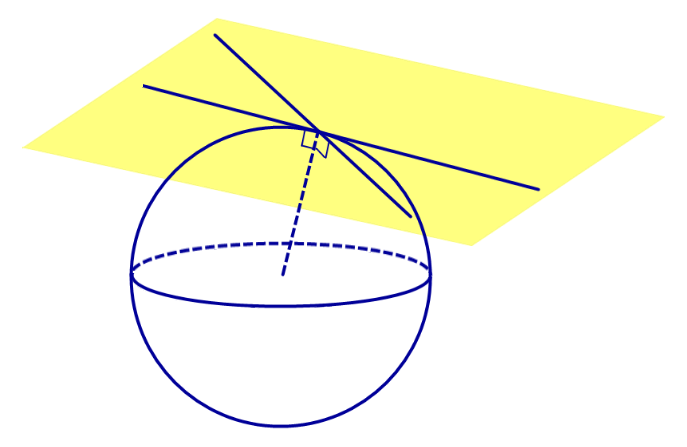
Касательная прямая к сфере. Касательная плоскость к сфере
Сфера, вписанная в цилиндр
Отношение объемов шара и цилиндра, описанного около сферы, ограничивающей этот шар
В цилиндр можно вписать сферу если
Призма. Прямоугольный параллелепипед
Сфера и шар
🌟 Видео

Видео:Видеоурок по математике "Цилиндр"Скачать

Сфера, описанная около цилиндра

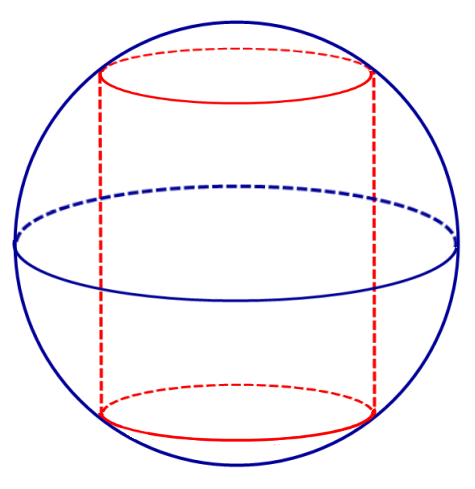
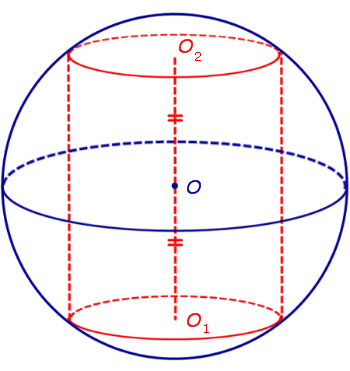
Определение 1. Цилиндром, вписанным в сферу, называют такой цилиндр, окружности оснований которого лежат на сфере (рис. 1).

Определение 2. Если цилиндр вписан в сферу, то сферу называют описанной около цилиндра.

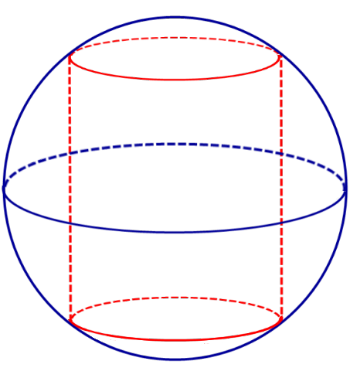
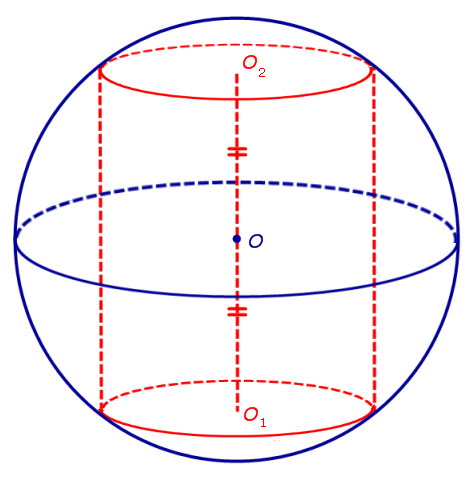
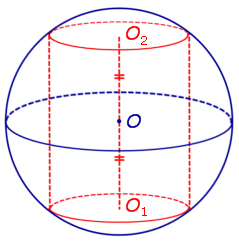
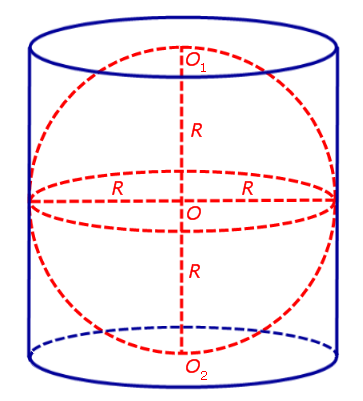
Утверждение. Около любого цилиндра можно описать сферу, причем только одну. Центр O этой сферы является серединой отрезка O₁O₂ , где O₁ и O₂ – центры оснований цилиндра (рис. 2)

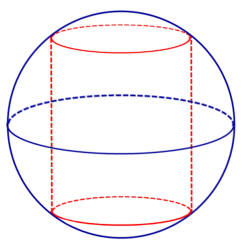
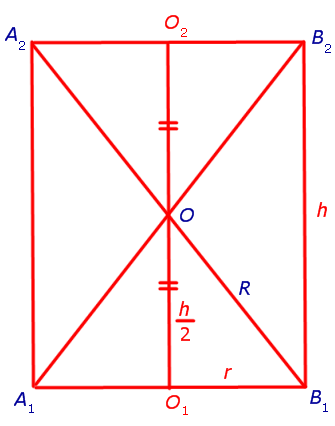
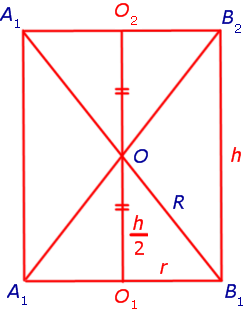
Доказательство. Обозначим буквами r и h радиус и высоту цилиндра и рассмотрим любое осевое сечение цилиндра (рис. 3).

Отрезки A₁A₂ и B₁B₂ , изображенные на рисунке 3, являются образующими цилиндра. Радиус R описанной сферы можно найти с помощью теоремы Пифагора из прямоугольного треугольника OB₁O₁ по формуле

Следствие 1. Радиус сферы, описанной около цилиндра с радиусом r и высотой h равен

Следствие 2. Отношение объема цилиндра к объему описанной около него сферы можно найти по формуле

Видео:11 класс, 19 урок, Сфера и шарСкачать

Сфера, вписанная в цилиндр

Видео:Шар вписан в цилиндр. Площадь поверхности шара равна 78. Найдите площадь полной поверхности цилиндраСкачать

Касательная прямая к сфере. Касательная плоскость к сфере

Определение 1. Прямую называют касательной к сфере (прямой, касающейся сферы), если эта прямая имеет со сферой единственную общую точку. Общую точку касательной прямой и сферы называют точкой касания (рис. 1).

Прямая касается сферы тогда и только тогда, когда эта прямая проходит через точку касания и перпендикулярна радиусу сферы, проведенному в точку касания.

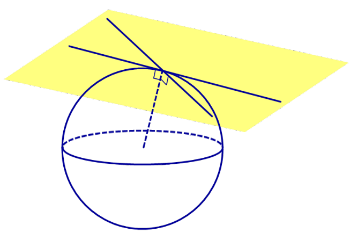
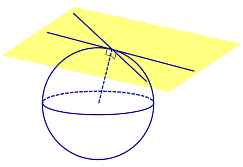
Множество всех прямых, касающихся сферы в некоторой точке, образуют касательную плоскость к сфере в этой точке (рис.2).

Плоскость касается сферы тогда и только тогда, когда плоскость и сфера имеют общую точку, причем только одну.

Плоскость касается сферы тогда и только тогда, когда плоскость и сфера имеют общую точку, причем плоскость перпендикулярна радиусу сферы, проведенному в эту точку.

Общую точку сферы и ее касательной плоскости называют точкой касания .

Видео:Цилиндр, конус, шар, 6 классСкачать

Сфера, вписанная в цилиндр

Определение 2. Сферой, вписанной в цилиндр, называют такую сферу, которая касается плоскостей обоих оснований цилиндра, а каждая образующая цилиндра является касательной к сфере (рис. 3).

Определение 3. Если сфера вписана в цилиндр, то цилиндр называют описанным около сферы .

Из рисунка 3 видно, что справедливы следующие два утверждения.

Утверждение 1. Около любой сферы можно описать цилиндр.

Утверждение 2. В цилиндр можно вписать сферу тогда и только тогда, когда высота цилиндра равна диаметру его основания.

Замечание. В том случае, когда в цилиндр можно вписать сферу, радиус вписанной сферы равняется радиусу основания цилиндра.

Видео:ЦИЛИНДР. КОНУС. ШАР. ЕГЭ. ЗАДАНИЕ 5.СТЕРЕОМЕТРИЯСкачать

Отношение объемов шара и цилиндра, описанного около сферы, ограничивающей этот шар

Задача. Найти отношение объемов шара и цилиндра, описанного около сферы, ограничивающей этот шар.

Видео:Сфера и шар. Сечение сферы. Вписанная и описанная сфераСкачать

В цилиндр можно вписать сферу если

Проверяемые элементы содержания и виды деятельности: владение понятиями о стереометрических фигурах; знание их свойств; знание формул для вычисления площадей поверхностей и объемов тел; умение применять эти знания при решении задач.

Ориентировочное время выполнения учащимися: 10—15 минут.

• Элементы, площадь поверхности, объем стереометрических фигур.

Особенности экзаменационных заданий по стереометрии

Задания этого вида представляют собой стереометрические задания на установление взаимосвязи между основными элементами многогранников и круглых тел, а также на использование формул для вычисления их площадей поверхностей и объемов. Вычислительной трудности задания не представляют; решение, как правило, сводится к использованию одной-двух формул. Соответствующие формулы нужно знать наизусть.

Куб — правильный многогранник, каждая грань которого представляет собой квадрат. Куб является частный случаем параллелепипеда и призмы, поэтому для него выполнены все их свойства. Кроме того, если а — длина ребра куба, — диагональ основания, — диагональ куба, — площадь полной поверхности, а V — объем куба, то справедливы формулы:

Видео:Объем шара и цилиндра. Практическая часть. 11 класс.Скачать

Призма. Прямоугольный параллелепипед

Призмой (n-угольной призмой) называется многогранник, две грани которого — равные n-угольники, лежащие в параллельных плоскостях, а остальные n граней — параллелограммы.

Правильной призмой называется прямая призма, основание которой — правильный многоугольник.

Прямой призмой называется призма, боковое ребро которой перпендикулярно плоскости основания. Высота прямой призмы равна ее боковому ребру, а все боковые грани прямой призмы — прямоугольники.

Соотношения для прямой призмы

Пусть H — высота прямой призмы, AA₁ — боковое ребро, — периметр основания, — площадь основания, — площадь боковой поверхности, — площадь полной поверхности, V — объем прямой призмы. Тогда имеют место следующие соотношения:

Особенности правильной шестиугольной призмы

В основании правильной шестиугольной призмы лежит правильный шестиугольник. Напомним его свойства.

— Сторона правильного шестиугольника равна радиусу описанной вокруг него окружности.

— Большая диагональ правильного шестиугольника является диаметром описанной вокруг него окружности и равна двум его сторонам.

— Меньшая диагональ правильного шестиугольника в раз больше его стороны.

— Угол между сторонами правильного шестиугольника равен 120°.

— Меньшая диагональ правильного шестиугольника перпендикулярна его стороне.

— Треугольник, образованный стороной шестиугольника, его большей и меньшей диагоналями, прямоугольный, а его острые углы равны 30° и 60°.

Пусть вне плоскости многоугольника задана точка P. Тогда фигура, образованная треугольниками , и многоугольником вместе с их внутренними областями называется пирамидой (n-угольной пирамидой).

Пирамида называется правильной, если ее основание — правильный многоугольник, а основание ее высоты — центр этого многоугольника.

Соотношения для правильной пирамиды

Пусть H — высота правильной пирамиды, h — ее апофема, — периметр основания пирамиды, — площадь основания, — площадь боковой поверхности, — площадь полной поверхности, V — объем правильной пирамиды. Тогда имеют место следующие соотношения:

Секущей плоскостью многогранника называется любая плоскость, по обе стороны от которой имеются точки данного многогранника. Секущая плоскость пересекает грани многогранника по отрезкам. Многоугольник, сторонами которого являются эти отрезки, называется сечением многогранника.

Тетраэдр имеет четыре грани, поэтому его сечениями могут быть только треугольники и четырехугольники (рис. 1). Параллелепипед имеет шесть граней. Его сечениями могут быть треугольники, четырехугольники, пятиугольники и шестиугольники (рис. 2).

Теоремы, используемые при построении сечений

Теорема 1. Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны. Поэтому секущая плоскость пересекает плоскости параллельных граней по параллельным прямым.

Теорема 2. Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой.

Теорема 3. Если прямая l параллельна какой либо прямой m, проведённой в плоскости то она параллельна и самой плоскости

Теорема 4. Если прямая, лежащая в плоскости сечения, не параллельна плоскости некоторой грани, то она пересекается со своей проекцией на эту грань.

Алгоритм построения сечений

Для построения сечений рекомендуем пользоваться следующим алгоритмом.

1. Если две точки секущей плоскости лежат в плоскости одной грани, то проводим через них прямую. Часть прямой, лежащая в плоскости грани — сторона сечения.

2. Если прямая a является общей прямой секущей плоскости и плоскости какой-либо грани, то находим точки пересечения прямой a с прямыми, содержащими ребра этой грани. Полученные точки — новые точки секущей плоскости, лежащие в плоскостях граней.

3. Если никакие две из данных точек не лежат в плоскости одной грани, то строим вспомогательное сечение, содержащее любые две данные точки, а затем выполняем шаги 1, 2.

Для контроля правильности построенного сечения, проверяйте, что:

— все вершины сечения лежат на рёбрах многогранника;

— все стороны сечения лежат в гранях многогранника;

— в каждой грани многогранника лежит не более одной стороны сечения.

Цилиндром называется фигура, полученная при вращении прямоугольника вокруг оси, содержащей его сторону.

Пусть h — высота цилиндра, r — радиус основания, S_бок — площадь боковой поверхности, S_полн — площадь полной поверхности, V — объем цилиндра. Тогда имеют место следующие соотношения:

Конусом называется фигура, полученная при вращении прямоугольного треугольника вокруг оси, содержащей его катет.

Пусть h — высота конуса, r — радиус основания, l — образующая, S_бок — площадь боковой поверхности, S_полн — площадь полной поверхности, V — объем конуса. Тогда имеют место следующие соотношения:

Видео:Почему площадь сферы в четыре раза больше её тени? [3Blue1Brown]Скачать

Сфера и шар

Шаром называется фигура, полученная при вращении полукруга вокруг оси, содержащей его диаметр. Сферой называется поверхность шара. Пусть R — радиус шара, S — площадь сферы, V — объем шара. Тогда имеют место следующие соотношения:

Комбинации круглых тел. Вписанные сферы

Сфера называется вписанной в цилиндр, если она касается обоих оснований цилиндра и каждой его образующей.

Сфера называется вписанной в конус, если она касается основания конуса и каждой его образующей.

Сфера называется вписанной в усечённый конус, если она касается обоих оснований конуса и всех его образующих.

Теорема 1: В прямой круговой цилиндр можно вписать сферу тогда и только тогда, когда его высота равна диаметру основания. Причём центр сферы есть середина оси цилиндра.

Теорема 2: В любой прямой круговой конус можно вписать сферу. Причём центр сферы есть точка пересечения оси конуса с биссектрисой угла наклона образующей конуса к плоскости его основания.

Теорема 3. В усечённый конус можно вписать сферу тогда и только тогда, когда он прямой круговой, и длина его образующей равна сумме длин радиусов оснований. Причём центр сферы есть середина оси усечённого конуса.

Комбинации круглых тел. Описанные сферы

Сфера называется описанной около цилиндра, если окружности его оснований лежат на сфере.

Сфера называется описанной около конуса, если вершина конуса и его основание лежат на сфере.

Теорема 1: около цилиндра можно описать сферу тогда и только тогда, когда он прямой круговой. Причём центр сферы есть середина оси цилиндра.

Теорема 2: около конуса можно описать сферу тогда и только тогда, когда он круговой. Причём центр сферы есть точка пересечения прямой, перпендикулярной к плоскости основания и проходящей через центр его, и плоскости, перпендикулярной какой-либо его образующей конуса и проходящей середину этой образующей.

Следствие: сферу можно описать около любого прямого кругового конуса. В этом случае, центр сферы — точка пересечения прямой, содержащей высоту конуса с плоскостью, перпендикулярной какой-либо из его образующих и проходящей через ее середину.

Комбинации конуса и цилиндра

Цилиндр называется вписанным в конус, если одно его основание лежит на основании конуса, а второе совпадает с сечением конуса плоскостью, параллельной основанию. Конус в этом случае называется описанным вокруг цилиндра.

Цилиндр называется описанным вокруг конуса, если центр одного из оснований цилиндра является вершиной вершина конуса, а противоположное основание цилиндра совпадает с основанием конуса. Конус в этом случае называется вписанным в цилиндр.

Комбинации многогранников и круглых тел. Описанные сферы

Сфера называется описанной около многогранника, если все его вершины лежат на этой сфере. Многогранник называется в этом случае вписанным в сферу.

Возможность описать сферу около многогранника означает существование точки (центра сферы), равноудалённой ото всех вершин многогранника.

Теорема 1: если из центра описанной около многогранника сферы опустить перпендикуляр на какое-либо из его рёбер, то основание этого перпендикуляра разделит ребро на две равные части.

Теорема 2: если из центра описанной около многогранника сферы опустить перпендикуляр на какую-либо из его граней, то основание этого перпендикуляра попадёт в центр круга, описанного около соответствующей грани.

Теорема 3: если около многогранника описана сфера, то её центр лежит на пересечении перпендикуляров к каждой грани пирамиды, проведённых через центр окружности, описанной около соответствующей грани.

Теорема 4: если около многогранника описана сфера, то её центр является точкой пересечений всех плоскостей, проведённых через середины рёбер пирамиды перпендикулярно к этим рёбрам.

Комбинации многогранников и круглых тел. Вписанные сферы

Сфера называется вписанной в многогранник, если все его грани касаются этой сферы. Многогранник называется в этом случае описанным около сферы.

Теорема: если в многогранник с площадью поверхности S и объёмом V вписан шар радиуса r, то справедливо соотношение:

Комбинации конуса, цилиндра и многогранников

В условиях задач встречаются также следующие понятия, не входящие в школьные учебники, которые уточняются непосредственно в условиях задач. Приведем наиболее употребительные из них.

Цилиндр вписан в призму: основания цилиндра вписаны в основания призмы.

Цилиндр описан вокруг призмы: основания цилиндра описаны вокруг оснований призмы.

Цилиндр вписан в пирамиду: одно из основание цилиндра вписано в сечение пирамиды плоскостью, параллельной основанию, а другое основание цилиндра принадлежит основанию пирамиды.

Цилиндр описан вокруг пирамиды: вершина пирамиды принадлежит одному из оснований цилиндра, а другое его основание описано вокруг основания пирамиды.

Конус вписан в призму: основание конуса вписано в основание призмы, а вершина конуса принадлежит противоположному основанию призмы.

Конус описан вокруг призмы: одно из оснований призмы вписано в сечение пирамиды плоскостью, параллельной основанию, а другое основание призмы вписано в основание конуса.

Конус вписан в пирамиду: их вершины совпадают, а основание конуса вписано в основание пирамиды. Вписать конус в пирамиду можно только тогда, когда апофемы пирамиды равны между собой.

Конус описан вокруг пирамиды: их вершины совпадают, а основание конуса описано вокруг основания пирамиды.