В цилиндр радиус основания которого равен 3 корня из 2

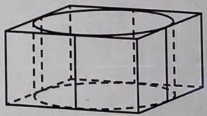
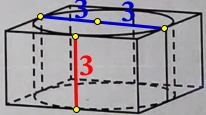
Найдите объем правильной треугольной призмы, вписанной в цилиндр, радиус основания которого равен \(2\sqrt 3\) , а высота равна \(3\sqrt 3\) .

Объем призмы равен произведению площади основания на высоту \(V=S_oH.\) Высота известна из условия и равна \(3\sqrt 3\) . Осталось найти площадь основания.

Так как призма правильная, то в основании лежит правильный треугольник. Площадь правильного треугольника можно найти через радиус описанной окружности \(S_o= R^2.\)

Тогда искомый объем равен \(V= (2\sqrt 3)^2*3\sqrt 3=81.\)

P.S. Можно не запоминать формулу площади правильного треугольника, так как здесь довольно просто можно вычислить длину стороны, зная радиус описанной окружности. Центр описанной окружности лежит в точке пересечения медиан. Медианы делятся точкой пересечения в отношении 2 к 1, считая от вершины. Из этих соображений находим длину медианы, а затем длину стороны и считаем площадь треугольника.

Пусть m — длина медианы (а в правильном треугольнике это высота и биссектрисса), тогда по определению синуса угла (а все углы в правильном треугольнике равны 60 градусам): \(sin60^o=m/a \Rightarrow a=m/sin60^o= m.\)

Так как медианы точкой пересечения делятся в отношении 2 к 1, считая от вершины, то \(R= m \Rightarrow m= R.\) Тогда \(a=\sqrt3R=6.\)

Площадь треуольника в основании равна \(S= a*a*sin60^o=9\sqrt 3\) , а тогда \(V=9\sqrt3*3\sqrt3=27*3=81.\)

Видео:#130. Задание 8: комбинация телСкачать

Найдите площадь боковой поверхности правильной

27065. Найдите площадь боковой поверхности правильной треугольной призмы, описанной около цилиндра, радиус основания которого равен √3, а высота равна 2.

Площадь боковой поверхности данной призмы равна сумме площадей всех боковых граней. Так как дана правильная треугольная призма, то все три грани являются прямоугольниками, площади которых равны.

Для нахождения площади боковой грани необходимо знать её высоту и длину ребра основания. Высота дана. Найдём длину ребра основания. Рассмотрим проекцию (вид сверху:

Читайте также: Цилиндр тормозной передний рабочий ваз 2112

Из прямоугольного треугольника АОС можем найти АС. По определению тангенса: Значит

Таким образом, сторона правильного треугольника выражается через радиус вписанной в него окружности как Значит площадь боковой поверхности будет равна: Ответ: 36

27066. Найдите площадь боковой поверхности правильной шестиугольной призмы, описанной около цилиндра, радиус основания которого равен √3, а высота равна 2.

Площадь боковой поверхности призмы равна произведению периметра снования и высоты. *Высота призмы равна высоте цилиндра. Вычислим сторону шестиугольника. Построим эскиз: Треугольник AOH равносторонний, Провели высоту OH, АН=НВ. Можем записать: Следовательно АВ=2. Таким образом, периметр шестиугольника равен 12, а искомая площадь 24 (периметр умножили на высоту призмы).

27107. Найдите площадь боковой поверхности правильной треугольной призмы, вписанной в цилиндр, радиус основания которого равен 2√3, а высота равна 2.

Площадь боковой поверхности призмы равна: Сторона правильного треугольника выражается через радиус описанной окружности как: Тогда площадь боковой поверхности призмы равна: Ответ: 36

27064. Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны 1. Найдите площадь боковой поверхности призмы.

Диаметр цилиндра равен стороне квадрата лежащего в основании, это 2. Тогда периметр квадрата равен 8. Площадь боковой поверхности равна 8∙1=8.

Видео:ЕГЭ 2022 математика задача 4 вариант 2Скачать

В цилиндр радиус основания которого равен 3 корня из 2

Шар вписан в цилиндр. Площадь полной поверхности цилиндра равна 18. Найдите площадь поверхности шара.

Радиусы шара и основания цилиндра равны. Площадь поверхности цилиндра, с радиусом основания r и высотой 2r равна

Площадь поверхности шара радиуса r равна то есть в 1,5 раза меньше площади поверхности цилиндра. Следовательно, площадь поверхности шара равна 12.

Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 1. Найдите объем параллелепипеда.

Высота параллелепипеда равна высоте вписанного в него цилиндра. Основанием параллелепипеда является квадрат, сторона которого в два раза больше радиуса вписанной в него окружности. Поэтому площадь основания равна 4, а объем параллелепипеда равен

Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 4. Объем параллелепипеда равен 16. Найдите высоту цилиндра.

Читайте также: Работа цилиндров двигателя 2115

Высота параллелепипеда равна высоте вписанного в него цилиндра. Основанием параллелепипеда является квадрат, сторона которого в два раза больше радиуса вписанной в него окружности. Поэтому сторона основания равна 8, а площадь основания равна 64. Тогда высота цилиндра равна

Почему получилось 64? Что-то не понятно:(

Длина диаметра цилиндра равна длине стороны квадрата в основании.

В куб вписан шар радиуса 1. Найдите объем куба.

Ребро куба равно диаметру вписанного в него шара, а объем куба равен кубу его ребра. Отсюда имеем:

В основании прямой призмы лежит прямоугольный треугольник с катетами 6 и 8. Боковые ребра равны Найдите объем цилиндра, описанного около этой призмы.

По теореме Пифагора длина гипотенузы треугольника в основании Поскольку гипотенуза является диаметром основания описанного цилиндра, его объем

Видео:Радиус основания цилиндра равен 26, а его образующая равна 9... Найдите площадь сечения.Скачать

В цилиндр радиус основания которого равен 3 корня из 2

В конус, радиус основания которого равен 3, вписан шар радиуса 1,5.

а) Изобразите осевое сечение комбинации этих тел.

б) Найдите отношение площади полной поверхности конуса к площади поверхности шара.

а) Осевым сечением является равнобедренный треугольник боковые стороны которого являются образующими конуса, а основанием — его диаметр, и вписанная в треугольник окружность, радиус которой равен радиусу шара (см. рис.).

б) Введём обозначения, как показано на рисунке. Пусть — центр вписанной окружности, отрезок — биссектриса угла и пусть имеем:

Тогда Для площадей поверхностей конуса и шара имеем: Тем самым, искомое отношение равно или 8:3.

при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки,

Видео:ЗАДАНИЕ 8 из ЕГЭ_53Скачать

Решение №2305 Цилиндр вписан в правильную четырёхугольную призму. Радиус основания и высота цилиндра равны 3.

Цилиндр вписан в правильную четырёхугольную призму. Радиус основания и высота цилиндра равны 3. Найдите площадь боковой поверхности призмы.

Источник: Ященко ЕГЭ 2022 (36 вар)

Правильной четырёхугольной призмой – называется шестигранник, в основаниях которого находятся 2 квадрата, а боковые грани представлены прямоугольниками.
Площадь боковой поверхности данной призмы – это площадь 4-х равных прямоугольников.
Длина прямоугольника равна диаметру цилиндра, ширина прямоугольника равна высоте цилиндра.

Найдём площадь боковой поверхности призмы:

S_{бок. поверх.} = 4·S_{прямоугольника} = 4· h ·( r + r ) = 4·3·(3 + 3) = 4·3·6 = 72

Видео:11 класс. Геометрия. Объем цилиндра. 14.04.2020Скачать

Нахождение радиуса цилиндра: формула и примеры

В данной публикации мы рассмотрим, как можно вычислить радиус цилиндра и разберем примеры решения задач для закрепления материала.

Видео:🔴 Даны два цилиндра. Радиус основания и высота ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 16 | ШКОЛА ПИФАГОРАСкачать

Формулы вычисления радиуса цилиндра

1. Через объем и высоту

Радиус цилиндра рассчитывается по формуле:

V – объем цилиндра; считается как произведение числа π на высоту фигуры на квадрат радиуса круга, являющего ее основанием.

• R – радиус основания цилиндра, т.е. окружности;
• π – число, округленное значение которого равняется 3,14.

2. Через площадь боковой поверхности

Радиус цилиндра считается таким образом:

S_бок. – площадь боковой поверхности цилиндра; равна произведению длины окружности (2 π R), являющейся основанием фигуры, на его высоту:

3. Через полную площадь поверхности

Данная формула получена следующим образом:

S – полная площадь поверхности фигуры, равная:

S = 2 π Rh + 2 π R 2 или S = 2 π R(h + R)

Возьмем первое выражение. Если перенести S в правую часть, получим:

2 π R 2 + 2 π Rh – S = 0

Можно заметить, что это квадратное уравнение вида ax 2 + bx + c = 0, где:

R является корнем данного уравнения (x). Подставив в стандартную формулу для расчета корней наши значения a, b и с получаем*:

* в нашем случае – только один положительный корень, т.к. радиус не может быть отрицательным.

Видео:Видеоурок по математике "Цилиндр"Скачать

Примеры задач

Задание 1
Высота цилиндра равняется 5 см, а объем – 141,3 см 3 . Вычислите его радиус.

Решение:
Воспользуемся соответствующей формулой, подставив в нее известные по условиям задачи значения:

Задание 2
Найдите радиус цилиндра, если площадь его боковой поверхности равна 175,84 см 2 , а высота составляет 7 см.

Решение:
Применим формулу, в которой задействованы заданные величины:

Задание 3
Рассчитайте радиус цилиндра, если полная площадь его поверхности – 602,88 см 2 , а высота – 10 см.

Решение:
Используем третью формулу для нахождения неизвестной величины:

🌟 Видео

🔴 Радиус основания цилиндра равен 15, а его ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 16 | ШКОЛА ПИФАГОРАСкачать

Задание 3 (часть 4) | ЕГЭ 2024 Математика (профиль) | ЦилиндрСкачать

ОБЪЕМ ЦИЛИНДРА #shorts #егэ #огэ #математика #профильныйегэСкачать

Стереометрия, номер 9.1Скачать

Геометрия Найдите площадь боковой поверхности правильной треугольной призмы, описанной околоСкачать

Как разобраться в корнях ? Квадратный корень 8 класс | Математика TutorOnlineСкачать

Параллелепипед описан около цилиндраСкачать

Все задания 16 ЕГЭ БАЗА из банка ФИПИ (математика Школа Пифагора)Скачать

ЗАДАНИЕ 8 из ЕГЭ_52Скачать

СЛИВ ЕГЭ ПО БАЗЕ 2024Скачать

Задания 11, 13 (часть 4) | ЕГЭ 2024 Математика (база) | Цилиндр, конусСкачать

🔴 Даны два конуса. Радиус основания и образующая ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 16 | ШКОЛА ПИФАГОРАСкачать

Егэ.11кл. Объём первого цилиндра равен 12 м³, у второго цилиндра высота в 3 раза больше,а основаниеСкачать