В цилиндр вписан квадрат найти его сторону (6 видео)

Содержание

Онлайн калькулятор длины стороны вписанного в круг квадрата. Как узнать длину стороны вписанного в круг квадрата.
В цилиндр вписан квадрат найти его сторону
В цилиндр вписан квадрат найти его сторону
Задача
Задача
Задача
Задача
В цилиндр вписан квадрат найти его сторону
В цилиндр вписан квадрат найти его сторону
🎦 Видео

Видео:11 класс. Геометрия. Объем цилиндра. 14.04.2020Скачать

Онлайн калькулятор длины стороны вписанного в круг квадрата. Как узнать длину стороны вписанного в круг квадрата.

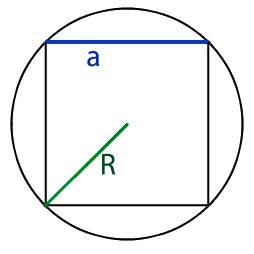
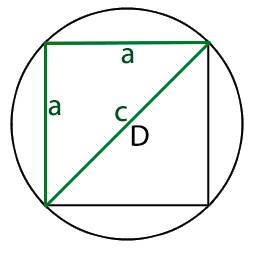
Для того что бы найти длину стороны вписанного в круг квадрата, нам необходимо узнать длину ребра этого квадрата. Для этого нам необходимо разделить квадрат по диагонали на два равнобедренных треугольника, при этом основание у этих треугольников будет равно диаметру круга.

Следующим действиям мы должны определиться с известной нам величиной круга в которую вписан квадрат, а именно нам должна быть известна:

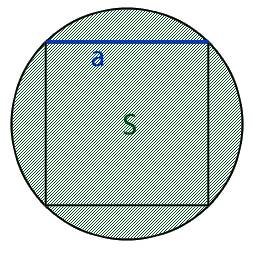
либо площадь круга, обозначаемая буквой S,
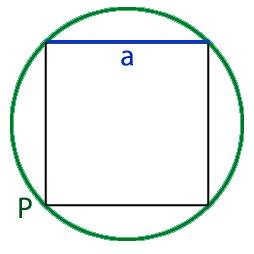
либо периметр круга, обозначаемый буквой P,
либо радиус круга, обозначаемый буквой R,
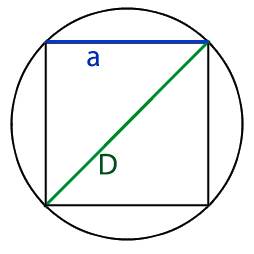
либо диаметр круга, обозначаемый буквой D.

Начнем по порядку, мы имеем равнобедренный прямоугольный треугольник и для того, что бы узнать длину его ребер нам необходимо воспользоваться теоремой Пифагора исходя из которой

Теперь для того что бы найти длину ребра треугольника (которое равно стороне нашего квадрата) нам необходимо узнать длину основания треугольника, которое равно диаметру круга

1. Если нам известна площадь круга в который вписан квадрат то для нахождения диаметра нам необходимо воспользоваться следующей формулой:

2. Если нам известна длина круга в который вписан квадрат то для нахождения диаметра нам необходимо воспользоваться следующей формулой:

3. Если нам известен радиус круга в который вписан квадрат то для нахождения диаметра нам необходимо воспользоваться следующей формулой:

Соответственно если мы знаем диаметр круга который равен основанию треугольника полученного путем разделения квадрата на две части по диагонали,

мы можем узнать длину сторон квадрата используя теорему Пифагора

Видео:Шар вписан в цилиндр. Площадь поверхности шара равна 78. Найдите площадь полной поверхности цилиндраСкачать

В цилиндр вписан квадрат найти его сторону

Шар вписан в цилиндр. Площадь полной поверхности цилиндра равна 18. Найдите площадь поверхности шара.

Радиусы шара и основания цилиндра равны. Площадь поверхности цилиндра, с радиусом основания r и высотой 2r равна

Площадь поверхности шара радиуса r равна то есть в 1,5 раза меньше площади поверхности цилиндра. Следовательно, площадь поверхности шара равна 12.

Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 1. Найдите объем параллелепипеда.

Высота параллелепипеда равна высоте вписанного в него цилиндра. Основанием параллелепипеда является квадрат, сторона которого в два раза больше радиуса вписанной в него окружности. Поэтому площадь основания равна 4, а объем параллелепипеда равен

Читайте также: Нумерация цилиндров рядного двигателя

Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 4. Объем параллелепипеда равен 16. Найдите высоту цилиндра.

Высота параллелепипеда равна высоте вписанного в него цилиндра. Основанием параллелепипеда является квадрат, сторона которого в два раза больше радиуса вписанной в него окружности. Поэтому сторона основания равна 8, а площадь основания равна 64. Тогда высота цилиндра равна

Почему получилось 64? Что-то не понятно:(

Длина диаметра цилиндра равна длине стороны квадрата в основании.

В куб вписан шар радиуса 1. Найдите объем куба.

Ребро куба равно диаметру вписанного в него шара, а объем куба равен кубу его ребра. Отсюда имеем:

В основании прямой призмы лежит прямоугольный треугольник с катетами 6 и 8. Боковые ребра равны Найдите объем цилиндра, описанного около этой призмы.

По теореме Пифагора длина гипотенузы треугольника в основании Поскольку гипотенуза является диаметром основания описанного цилиндра, его объем

Видео:Шар вписан в цилиндр. Площадь полной поверхности цилиндра равна 18. Найдите площадь поверхности шараСкачать

В цилиндр вписан квадрат найти его сторону

Видео:Задание 2|ЕГЭ ПРОФИЛЬ| СТЕРЕОМЕТРИЯ| Цилиндр вписан в прямоугольный параллелепипед.Радиус основанияСкачать

Задача

Осевое сечение цилиндра — квадрат, диагональ которого равна 4√2.
Вычислить объем цилиндра.

Решение.
Поскольку диагональ сечения цилиндра — квадрат, то обозначим его сторону как a.
a 2 + a 2 = (4√2) 2
2a 2 = 32
a 2 = 16
a = 4

Объем цилиндра найдем по формуле:
V = πd 2 / 4 * h
откуда
V = π4 2 / 4 * 4
V = 16π

Ответ: Объем цилиндра равен 16π

Видео:Куб и цилиндр. Практическая часть. 11 класс.Скачать

Задача

Куб с ребром длиной а вписан в цилиндр. Найдите площадь осевого сечения цилиндра.

Решение.
Проведем плоскость через основание цилиндра.

Диагональ куба является одновременно диаметром цилиндра. Зная сторону куба, определяем длину диагонали AC квадрата ABCD как
CD 2 + AD 2 = AC 2
a 2 + a 2 = AC 2
2a 2 = AC
AC = a√2

Проведем плоскость через ось цилиндра по диагонали AC. Высота сечения равна длине ребра куба и по условиям задачи рана а, а ширина сечения равна a√2.
Таким образом, площадь сечения равна:

Видео:Геометрия Высота цилиндра 2 м радиус оснований 7 м В этот цилиндр наклонно вписан квадрат такСкачать

Задача

Диагональ осевого сечения цилиндра равна 12 см и образует с плоскостью нижнего основания угол 45 градусов. Найти обьём цилиндра.

Решение.
Поскольку основание осевого сечения образует с высотой цилиндра, принадлежащей сечению, прямой угол, то треугольник, который образован диагональю осевого сечения, высотой цилиндра и его диаметром — прямоугольный.

Исходя из этого, угол между диагональю и высотой также равен 45 градусов ( 180 — 90 — 45 ).

Таким образом, треугольник является равнобедренным, а, следовательно, высота цилиндра равна его диаметру. Применив теорему Пифагора, найдем их.

Теперь применим формулу объема цилиндра V = пd 2 / 4 h

Видео:Геометрия Цилиндр описан около шара. Найдите объем шара, если известно, что объем цилиндра равен 60.Скачать

Задача

Высота цилиндра 2м. Радиус основания 7м. В этот цилиндр наклонно вписан квадрат так, что все вершины его лежат на окружностях оснований. Найти сторону квадрата.

Висота циліндра 2м. Радіус основи 7м. В цей циліндр похило вписаний квадрат так, що всі вершини його лежать на окружностях основ. Знайти сторону квадрата.

Пусть d – диагональ квадрата. Тогда сторона квадрата а равна:

Позначимо d – діагональ квадрата. Тоді сторона квадрата а :

Видео:РЕШЕНИЕ ЗАДАЧ НА ЦИЛИНДРСкачать

В цилиндр вписан квадрат найти его сторону

Шар вписан в цилиндр. Площадь полной поверхности цилиндра равна 18. Найдите площадь поверхности шара.

Высота параллелепипеда равна высоте вписанного в него цилиндра. Основанием параллелепипеда является квадрат, сторона которого в два раза больше радиуса вписанной в него окружности. Поэтому сторона основания равна 8, а площадь основания равна 64. Тогда высота цилиндра равна

Почему получилось 64? Что-то не понятно:(

Длина диаметра цилиндра равна длине стороны квадрата в основании.

В куб вписан шар радиуса 1. Найдите объем куба.

Ребро куба равно диаметру вписанного в него шара, а объем куба равен кубу его ребра. Отсюда имеем:

Видео:Призма и цилиндр. Практическая часть. 11 класс.Скачать

В цилиндр вписан квадрат найти его сторону

Шар вписан в цилиндр. Площадь полной поверхности цилиндра равна 18. Найдите площадь поверхности шара.

В куб вписан шар радиуса 1. Найдите объем куба.

В основании прямой призмы лежит квадрат со стороной 2. Боковые ребра равны Найдите объем цилиндра, описанного около этой призмы.

Цилиндр и конус имеют общие основание и высоту. Объём конуса равен 25. Найдите объём цилиндра.

Из единичного куба вырезана правильная четырехугольная призма со стороной основания 0,5 и боковым ребром 1. Найдите площадь поверхности оставшейся части куба.

Цилиндр и конус имеют общие основание и высоту. Найдите объем конуса, если объем цилиндра равен 150.

Объём куба, описанного около сферы, равен 216. Найдите радиус сферы.

Конус описан около правильной четырехугольной пирамиды со стороной основания 4 и высотой 6. Найдите его объем, деленный на

Во сколько раз объем конуса, описанного около правильной четырехугольной пирамиды, больше объема конуса, вписанного в эту пирамиду?

В куб с ребром 3 вписан шар. Найдите объем этого шара, деленный на

Около куба с ребром описан шар. Найдите объем этого шара, деленный на

Вершина A куба с ребром 1,6 является центром сферы, проходящей через точку A₁. Найдите площадь S части сферы, содержащейся внутри куба. В ответе запишите величину