В цилиндр вписан тупоугольный треугольник

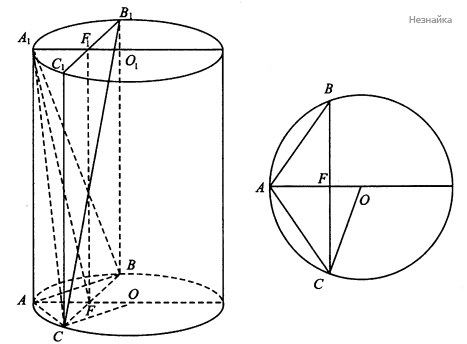
В основание цилиндра высотой 24 и радиусом основания 8 вписан тупоугольный треугольник АВС, в котором ВС = 12, АВ = АС.

а) Постройте сечение призмы ABCA₁B₁C₁ плоскостью, перпендикулярной плоскостям BB₁C₁C и А₁ВС и проходящей через точку А, если АА₁, BB₁ и CC₁ — образующие цилиндра

б) Найдите величину угла между плоскостями (B₁BC) и (A₁BC).

а) Пусть [math]O[/math] и [math]O_1[/math] — центры оснований цилиндра, тогда [math]F[/math] и [math]F_1[/math] — середины хорд [math]BC[/math] и [math]B_1C_1[/math] соответственно (см. рисунок). Покажем, что [math]AFF_1[/math] — искомая плоскость. [math]A_1F[/math] — медиана, а значит, и высота равнобедренного треугольника [math]A_1BC[/math]. [math]FF_ \parallel\;BB_1[/math], значит, [math]FF_ \perp\;(ABC)[/math] и, в частности, [math]FF_ \perp\;BC[/math]. Итак, [math]FF_ \perp\;BC[/math] и [math]A_1F\;\perp\;BC[/math], тогда [math](AFF_1)\perp BC[/math], откуда [math](AFF_1)\perp A_1BC[/math] и [math](AFF_1)\perp BB_1C_1C[/math]. Сечением призмы [math]ABCA_1B_1C_1[/math] плоскостью [math]AFF_1[/math] является прямоугольник [math]ADD_1A_1[/math]

б) Угол между плоскостями [math]B_1BC[/math] и [math]A_1BC[/math] — это угол [math]A_1FF_1:[/math]

[math]A_1F\;\in\;(A_1BC)[/math], [math]FF_1\;\in\;(B_1BC)[/math]. [math]\bigtriangleup A_1CB\;[/math] — равнобедренный, [math]\;A_1F\perp BC,[/math] [math]B_1BCC_1[/math] — прямоугольник, [math]FF_1\;\parallel\;BB_1[/math] и [math]FF_1\;\perp\;BC[/math], отсюда [math]\angle A_1FF_1[/math] — линейный угол двугранного угла между плоскостями [math]A_1CB[/math] и [math]B_1BC[/math].

Из [math]\bigtriangleup A_1FF_1[/math]: [math]\angle A_1F_1F=90^\circ[/math] [math]tg\angle A_1FF_1=\frac [/math]; [math]A_1F_1=AF;\;AF=AO-FO.[/math]

Из [math]\bigtriangleup OFC[/math], где [math]\angle OFC=90^\circ[/math], [math]FC=6,[/math] найдем [math]FO=\sqrt =2\sqrt7[/math]. [math]AF=8-2\sqrt7.[/math]

Видео:Задача, которую боятсяСкачать

Регистрация Вход Форум Поиск FAQ alexlarin.net

Видео:ТРИ ПРИЗНАКА РАВЕНСТВА ТРЕУГОЛЬНИКОВ НА ЕГЭ #shorts #математика #егэ #огэ #профильныйегэ #геометрияСкачать

В основание цилиндра высотой

В основание цилиндра высотой

В основание цилиндра высотой

В основание цилиндра высотой 24 и радиусом основания 8 вписан тупоугольный треугольник АВС, в котором ВС = 12, АВ = АС.

а) Постройте сечение призмы ABCA1B1C1 плоскостью, перпендикулярной плоскостям BB1C1C и А1ВС и проходящей через точку А, если АА1, BB1 и CC1 — образующие цилиндра

Пожалуйста, объясните глупому человеку, как такое возможно? Ведь BB1C1C и А1ВС не параллельные и не совпадающие плоскости?
б) Найдите величину угла между плоскость B1BC и A1BC.
Для этого ведь надо найти боковую сторону, верное? Но как это сделать?

Читайте также: Чем сжать цилиндр суппорта

В основание цилиндра высотой 24 и радиусом основания 8 вписан тупоугольный треугольник АВС, в котором ВС = 12, АВ = АС.

а) Постройте сечение призмы ABCA1B1C1 плоскостью, перпендикулярной плоскостям BB1C1C и А1ВС и проходящей через точку А, если АА1, BB1 и CC1 — образующие цилиндра

Пожалуйста, объясните глупому человеку, как такое возможно? Ведь BB1C1C и А1ВС не параллельные и не совпадающие плоскости?
б) Найдите величину угла между плоскость B1BC и A1BC.
Для этого ведь надо найти боковую сторону, верное? Но как это сделать?

Видео:7 класс, 32 урок, Остроугольный, прямоугольный и тупоугольный треугольникиСкачать

В основании цилиндра высотой 24 и радиусом основания 8 вписан тупоугольный треугольник АВС, в котором ВС = 12, АВ = АС?

В основании цилиндра высотой 24 и радиусом основания 8 вписан тупоугольный треугольник АВС, в котором ВС = 12, АВ = АС.

А) Постройте сечение призмы АВСА1В1С1 плоскостью, перпендикулярной плоскостям ВВ1С1С А1ВС и проходящей через точку А, если АА1, ВВ1 И СС1 — образующие цилиндра.

Б) Найдите величину угла плоскостью В1ВС и А1ВС.

Пожалуйста, объясните как сделать.

К двум плоскостям, имеющим общую линию их пересечения ВС, перпендикулярнаяплоскость проходит по перпендикуляру к их линии пересечения.

Основание пересекается по диаметру АОД (то есть через ось цилиндра, в который вписана призма).

расстояние стороны ВС от диаметра равно к = √(8² — (12 / 2)²) = √64 — 36) = √28 = 2√7.

Расстояние от точки А до стороны ВС равно 8 — 2√7.

В сечении будет прямоугольник с основанием 8 — 2√7 и высотой 24 (по высоте цилиндра и призмы.

Б) Угол между заданными плоскостямиα = arc tg (8 — 2√7) / 24 =

Видео:11 класс. Геометрия. Объем цилиндра. 14.04.2020Скачать

Радиус основания цилиндра — 6 см, высота — 5см?

Радиус основания цилиндра — 6 см, высота — 5см.

Найдите угол наклона диагонали осевого сечения к плоскости основания цилиндра.

Видео:✓ Задача про цилиндр | ЕГЭ-2018. Задание 14. Математика. Профильный уровень | Борис ТрушинСкачать

АВСА1В1С1 — прямая треугольная призма , основанием которой является равнобедренный треугольник АВС (уг?

АВСА1В1С1 — прямая треугольная призма , основанием которой является равнобедренный треугольник АВС (уг.

Точка F — внутренняя точка отрезка АА1 .

Вычислите площадь сечения призмы плоскостью , проходящей через точки F , В, С, если известно , что СС1 = 2 см, площадь боковой поверхности призмы равна(12 + 6√2)см², а плоскость сечения составляет с плоскостью основания угол, градусная мера которого равна 30.

Видео:Видеоурок по математике "Цилиндр"Скачать

Диагональ осевого сечения цилиндра наклонена к плоскости основания под углом 60° и равна 20 см?

Диагональ осевого сечения цилиндра наклонена к плоскости основания под углом 60° и равна 20 см.

Найдите высоту, радиус основания цилиндра, длину окружности основания и площадь боковой поверхности цилиндра.

Видео:Куб и цилиндр. Практическая часть. 11 класс.Скачать

Помогите?

Дан цилиндр, радиус основания которого равен 10, а полная площадь его поверхности равна 660п.

На окружностях разных оснований цилиндра отмечены точки А и В таким образом, что площадь сечения цилиндра, параллельного оси цилиндра и проходящего через эти точки, равна 276.

Найдите расстояние между плоскостью сечения и осью цилиндра.

Видео:Призма и цилиндр. Практическая часть. 11 класс.Скачать

Диаметр окружности основания кругового цилиндра равен 26?

Диаметр окружности основания кругового цилиндра равен 26.

Образующая цилиндра равна 21.

Плоскость пересекает основания цилиндра по хордам длины 24 и 10.

Найдите тангенс угла между этой плоскостью и плоскостью основания цилиндра.

Видео:9 класс, 41 урок, ЦилиндрСкачать

Помогите, пожалуйста?

Радиус основания цилиндра равен 3.

Найти диагональ осевого сечения цилиндра, если она наклонена к плоскости основания цилиндра под углом 60 градусов.

Видео:удаление неизвестного объектаСкачать

1. Основанием пирамиды DABC является правильный треугольник АВС, сторона которого равна а?

1. Основанием пирамиды DABC является правильный треугольник АВС, сторона которого равна а.

Ребро DA перпендикулярно к плоскости АВС, а плоскость DBC составляет с плоскостью АВС угол в 30°.

Найдите площадь боковой поверхности пирамиды.

Видео:Миникурс по геометрии. Куб, призма, цилиндр и конусСкачать

Высота цилиндра 8дм, радиус основания 5дм?

Высота цилиндра 8дм, радиус основания 5дм.

Цилиндр пересечен плоскостью параллельно оси так.

Что в сечении получился квадрат.

Найдите расстояния от этого сечения до оси цилиндра.

Видео:Разбор 36 вариантов Ященко. Вариант 21Скачать

Основанием пирамиды давс является правильный треугольник авс, сторона которого равна а?

Основанием пирамиды давс является правильный треугольник авс, сторона которого равна а.

Ребро да перпендикулярно к плоскости авс, а плоскость двс составляет с плоскостью авс угол 30гр.

Найдите площадь боковой поверхности пирамиды.

Видео:Построение треугольника по углу и двум сторонам. 7 класс.Скачать

Диагональ сечения цилиндра, параллельного оси, наклонена к плоскости основания под углом 30°?

Диагональ сечения цилиндра, параллельного оси, наклонена к плоскости основания под углом 30°.

Найдите площадь сечения, если радиус цилиндра равен 6 см, а хорда, по которой плоскость сечения пересекает основание, стягивает дугу в 60°.

На этой странице сайта, в категории Геометрия размещен ответ на вопрос В основании цилиндра высотой 24 и радиусом основания 8 вписан тупоугольный треугольник АВС, в котором ВС = 12, АВ = АС?. По уровню сложности вопрос рассчитан на учащихся 10 — 11 классов. Чтобы получить дополнительную информацию по интересующей теме, воспользуйтесь автоматическим поиском в этой же категории, чтобы ознакомиться с ответами на похожие вопросы. В верхней части страницы расположена кнопка, с помощью которой можно сформулировать новый вопрос, который наиболее полно отвечает критериям поиска. Удобный интерфейс позволяет обсудить интересующую тему с посетителями в комментариях.

Начертим отрезки BE и CE, тогда получается три равноправных треугольника у которых площади равны, тогда площадь каждого из них = 144 / 3 = 48, а образовавшийся трапеция равна двум треугольникам, тогда площадь трапеции равна = 2 * 48 = 96.

Решение задания смотри на фотографии.

Я так понимаю в условии описка и высота (не вершина) пирамиды равна 5см. В основании правильной четырехугольной пирамиды SABCD лежит правильный четырехугольник (квадрат) ABCD со сторонами AB = BC = CD = AD = 10 cм. Боковыми гранями данной пирамиды ..

Подставляешь значения x и все. Т. е, например 3x — 5, нужно подставить — 3, = >3 * ( — 3) — 5 = — 9 — 5 = — 14. Пишу ответы через пробел, слева — направо, сверху — вниз. — 14 — 11 — 8 — 5 — 2 1 4 14 11 8 5 2 — 1 — 4 — 6 — 4 — 2 0 2 4 6.

Видео:ЕГЭ 2022 задача 3 вариант 1 планиметрияСкачать

Тупоугольный треугольник, элементы, свойства, признаки и формулы

Видео:Планиметрия с нуля и до уровня ЕГЭ 2024 за 4 часа | Вся теория по №1,17 | Математика профильСкачать

Тупоугольный треугольник, элементы, свойства, признаки и формулы.

Тупоугольный треугольник – это треугольник, у которого один угол тупой.

Видео:Цилиндр, конус, шар, 6 классСкачать

Тупоугольный треугольник (понятие и определение):

Тупоугольный треугольник – это треугольник, у которого один угол тупой, т.е. один из его углов лежит в пределах между 90° и 180°.

Тупоугольный треугольник – это треугольник, у которого один угол тупой, а два других – острые. В свою очередь, тупой угол – это угол, градусная мера которого составляет 90° до 180°, а острый угол – это угол, градусная мера которого составляет менее 90 градусов

Рис. 1. Тупоугольный треугольник

∠ BАC– тупой угол треугольника,

По определению, тупоугольным треугольником не может быть правильный (равносторонний) треугольник , т.к. у него каждый угол составляет 60°.

Рис. 2. Равносторонний треугольник

АВ = ВС = АС – стороны треугольника,

По определению, тупоугольным треугольником не может быть прямоугольный треугольник , т.к. у него один угол составляет 90° и сумма двух других углов также составляет 90°.

Рис. 3. Прямоугольный треугольник

Тупоугольный треугольник также может быть одновременно равнобедренным треугольником . Но не всякий равнобедренный треугольник тупой.

Рис. 4. Равнобедренный треугольник

АВ = AС – боковые стороны, BС – основание,

Хотя в тупоугольном треугольнике тупой угол больше 90 градусов, сумма углов в треугольнике всегда равна 180 градусам.

Видео:11 класс, 32 урок, Объем цилиндраСкачать

Элементы тупоугольного треугольника:

Кроме сторон и углов у тупоугольного треугольника также имеются внешние углы. Внешний угол это угол, смежный с внутренним углом треугольника. У любого треугольника, в т.ч. тупоугольного, 6 внешних углов, по 2 на каждый внутренний. Внешний угол тупого угла тупоугольного треугольника всегда будет острым углом. Внешний угол острого угла тупоугольного треугольника всегда будет тупым углом.

Рис. 5. Тупоугольный треугольник и внешний угол

Медиана тупоугольного треугольника (как и любого другого треугольника), соединяющая вершину треугольника с противоположной стороной, делит ее пополам, т.е. на два одинаковых отрезка.

Рис. 6. Тупоугольный треугольник и медиана тупоугольного треугольника

MA – медиана тупоугольного треугольника

Все три медианы треугольника пересекаются в одной точке, которая называется центроидом или центром тяжести треугольника, и делятся этой точкой на две части в отношении 2:1, считая от вершины.

Рис. 7. Тупоугольный треугольник и высота тупоугольного треугольника

MС – высота тупоугольного треугольника

Высота тупоугольного треугольника может лежать за пределами треугольника.

Биссектриса в тупоугольном треугольнике (как и в любом другом треугольнике) делит угол пополам. Биссектрисы пересекаются в точке, которая является центром вписанной окружности.

Рис. 8. Тупоугольный треугольник и биссектриса угла тупоугольного треугольника

MA – биссектриса тупого угла тупоугольного треугольника

Кроме того, биссектриса тупоугольного треугольника (как и любого другого треугольника) делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника

Видео:Линия пересечения двух поверхностей конус и цилиндр (Метод секущих плоскостей)Скачать

Свойства тупоугольного треугольника:

Свойства тупоугольного треугольника аналогичны свойствам обычного треугольника:

1. Против большей стороны лежит больший угол, и наоборот.

Рис. 9. Тупоугольный треугольник

2. Против равных сторон лежат равные углы, и наоборот.

Рис. 10. Тупоугольный треугольник с равными боковыми сторонами

3. Сумма углов тупоугольного треугольника равна 180°.

4. Любая сторона тупоугольного треугольника меньше суммы двух других сторон и больше их разности: