В цилиндр вписан усеченный конус (2 видео)

@ Часто встречаются и представляют интерес задачи, в которых взаимодействуют тела вращения с телами вращения и многогранниками.

Сфера называется описанной около цилиндра (конуса), если окружности его оснований (окружность его основания и вершина) принадлежат сфере.

Около любого цилиндра и любого конуса можно описать сферу.

Сфера называется вписанной в цилиндр , если она касается каждой образующей и обоих оснований цилиндра.

В цилиндр можно вписать сферу тогда и только тогда, когда его высота равна диаметру основания.

Центр сферы является серединой отрезка, соединяющего центры оснований.

Сфера называется вписанной в конус , если она касается образующих конуса и его основания.

В любой конус можно вписать сферу.

Сфера называется вписанной в усеченный конус , если она касается всех образующих и обоих оснований конуса.

Очевидно справедливо утверждение: в усеченный конус можно вписать сферу тогда и только тогда, когда образующая усеченного конуса равна сумме радиусов оснований. Тогда диаметр сферы равен высоте усеченного конуса.

Понятия вписанная и описанная сферы и вписанный и описанный шары в задачах не различаются.

Цилиндр называется вписанным в конус , если одно его основание принадлежит основанию конуса, а второе совпадает с сечением конуса плоскостью, параллельной основанию.

Основание цилиндра и основание конуса – концентрические круги.

Во всякий конус можно вписать цилиндр. Его высота меньше высоты конуса.

Цилиндр называется вписанным в усеченный конус , если одно его основание принадлежит основанию конуса, а другое совпадает со вторым основанием конуса. Высота такого цилиндра равна высоте усеченного конуса.

Так как цилиндр и конус однозначно определяются двумя независимыми параметрами, то, задав два независимых параметра одной фигуры и один параметр другой (вписанной или описанной), можно найти остальные параметры.

1 . В конус высоты Н и радиуса R вписан цилиндр высоты h . Найти радиус основания цилиндра.

Шар задается однозначно одним параметром, поэтому, задав параметр шара и один из независимых параметров вписанного или описанного конуса или цилиндра, можно найти другой параметр.

Или же по двум независимым параметрам конуса или цилиндра можно определить параметр вписанного или описанного шара.

2. В конус высоты Н и радиуса R вписан шар. Найти радиус шара.

3. В усеченный конус, радиусы оснований которого R и r , вписан шар. Найти его радиус.

4. В шар радиуса R вписан цилиндр высоты Н . Найти радиус его основания.

Пример 7.6.2. (КубГУ, матем., 1971 г.)

В прямой конус с образующей 1 и углом 2 a при вершине осевого сечения вписан шар. Вычислить радиус окружности, по которой соприкасаются поверхности конуса и шара, а также объем и полную поверхность меньшей из частей шара, на которые он рассекается кругом упомянутого радиуса. Решение

Решение задач о вписанных телах вращения, как правило, сводится к планиметрическим. Поэтому сделаем чертеж осевого сечения конуса. Тогда сфера будет окружностью большого круга, вписанной в равнобедренный треугольник. Отрезок прямой, параллельной основанию, соединяющий точки касания окружности и треугольника, будет диаметром искомой окружности.

Из прямоугольного треугольника ACD имеем AD = 1 sin a .

АО – биссектриса угла CAD , следовательно, .

Из прямоугольного треугольника AOD находим , OD = OM как радиусы.

D MKO подобен D CMO , следовательно, KMO = a

Меньшая часть шара – шаровой сегмент, высота которого РК . Его объем и площадь поверхности вычисляются по формулам

Тогда PK = PO — OK . Подставив найденные величины и преобразовав, получим ,

Пример 7.6.3. (КубГУ, матем., 1979 г.)

Пример 7.6.4. (КубГУ, матем., 1986 г.)

В усеченный конус вписан шар, касающийся обоих оснований и боковой поверхности. Найти длину образующей усеченного конуса, если даны его высота h и радиус a окружности касания. Решение

Сделаем чертеж осевого сечения. Тогда MK = a , BP = h . Так как высота конуса равна диаметру шара, то . Р OMK = Р ABP , как острые углы со взаимно перпендикулярными сторонами. Тогда D OMK подобен D ABP и имеет место соотношение , откуда .

Ответ: .

Пример 7.6.5. (КубГУ, эконом., 1989 г.)

Пусть AC = a , тогда из чертежа осевого сечения находим CD = a tg a , .

Разделив обе части на , получим .

Из прямоугольного треугольника имеем , тогда

Пример 7.6.6. (КубГУ, матем., 1979 г.)

В усеченный конус вписан шар радиуса R . Образующая конуса наклонена к плоскости нижнего основания под углом ( a 90°) . Найти объем усеченного конуса. Решение

В шар радиуса R вписан конус. Угол между образующей конуса и плоскостью основания равен a . В конус вписан шар. Найти радиус вписанного шара. Решение

В осевом сечении конуса получили равнобедренный треугольник с вписанной и описанной окружностями. Отметим, что центры вписанной и описанной окружностей совпадают только у правильного треугольника. Если угол при вершине равнобедренного треугольника меньше 60° , то центр описанной окружности расположен на высоте ближе к этой вершине, чем центр вписанной окружности. Если треугольник прямоугольный, то центр описанной окружности совпадает с серединой гипотенузы, если же треугольник тупоугольный, то центр описанной окружности будет расположен вне треугольника, в то время как центр вписанной окружности для любого треугольника является внутренней точкой.

Если О – центр вписанной окружности, то АО биссектриса D CAD и из треугольника OAD находим .

Пример 7.6.8. (КубГУ, физич., 1979 г.)

Шар радиуса R вписан в конус. Из центра шара образующая конуса видна под углом a . Найти объем конуса. Решение

Пусть О – центр вписанной окружности в осевом сечении конуса. По условию Р AOC = a , тогда Р AOD = 180° — a . Очевидно, что a > 90° . Из прямоугольного треугольника AOD находим Р OAD = 180° — (90° + 180° -a) = a — 90° . АО – биссектриса Р CAD . Следовательно, Р CAD = 2 Р OAD = 2 a — 180° .
OD =R . Тогда из треугольника AOD находим AD. AD = OD tg AOD = R tg( 180° -a ) = — R tg a .

Из треугольника AСD находим СD

Подставив найденные величины в формулу объема, получим

Если 90° a 135° , то 180° a 270° ; тогда tg a , tg 2 a >0 и .

Если 135° a 180° , то 270° a 360° ; тогда tg 2 a , tg 2 a и .

Содержание

Конус, вписанный в цилиндр
Конус, вписанный в цилиндр
Отношение объемов конуса и описанного около него цилиндра
Геометрия. 11 класс
💥 Видео

Видео:Конус. 11 класс.Скачать

Конус, вписанный в цилиндр

Видео:Шар, вписанный в цилиндр, конус, усеченный конус.Скачать

Конус, вписанный в цилиндр

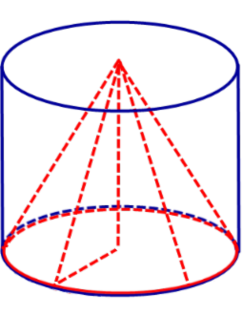
Определение 1. Конусом, вписанным в цилиндр, называют такой конус, у которого основание совпадает с одним из оснований цилиндра, а вершина совпадает с центром другого основания цилиндра (рис. 1).

Определение 2. Если конус вписан в цилиндр, то цилиндр называют описанным около конуса.

Замечание. Высота конуса равна высоте цилиндра, описанного этого конуса.

Утверждение. Около любого конуса можно описать цилиндр.

Доказательство. Для доказательства достаточно построить цилиндр, у которого одно из оснований совпадает с основанием конуса, а плоскость другого основания проходит через вершину конуса.

Видео:Усеченный конус. 11 класс.Скачать

Отношение объемов конуса и описанного около него цилиндра

Утверждение. Объем конуса в 3 раза меньше объема описанного около него цилиндра.

Доказательство. Пусть радиус основания конуса равен r, а высота конуса равна h. Поскольку цилиндр описан около конуса, то радиус основания цилиндра также равен r, а высота цилиндра равна h. Тогда объем конуса равен

Видео:Как сделать усеченный конус мастер класс от Дачного мастера на все рукиСкачать

Геометрия. 11 класс

Конспект урока

Урок №10. Комбинации тел вращения

Перечень вопросов, рассматриваемых в теме:

комбинации конуса и цилиндра, конуса и усеченного конуса, цилиндра и усеченного конуса, нескольких сфер;
цилиндр, описанный около конуса, конус, описанный около цилиндра, усеченный конус, описанный около конуса и цилиндра;
цилиндр, вписанный в конус, конус, вписанный в цилиндр, усеченный конус, вписанный в конус и цилиндр.

Цилиндр вписан в конус, если одно основание цилиндра лежит в плоскости основания конуса, а окружность другого основания — на боковой поверхности конуса. Конус, соответственно, в этом случае называется описанным около цилиндра.

Конус вписан в цилиндр, если основание конуса совпадает с основанием цилиндра, а вершина совпадает с центром другого основания цилиндра. Цилиндр, соответственно, в этом случае называется описанным около конуса.

Конус вписан в другой конус, если его вершина лежит в центре основания второго конуса, а основание лежит на боковой поверхности.

Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. и др. Геометрия. 10–11 классы : учеб. для общеобразоват. организаций : базовый и углубл. уровни – М. : Просвещение, 2014. – 255, сс. 136-147.

Шарыгин И.Ф., Геометрия. 10–11 кл. : учеб. для общеобразоват. учреждений – М.: Дрофа, 2009. – 235, : ил., ISBN 978–5–358–05346–5, сс. 77-84.

Открытые электронные ресурсы:

Теоретический материал для самостоятельного изучения

1. Комбинации цилиндра и конуса

В любой конус можно вписать цилиндр.

Оси конуса и вписанного в него цилиндра совпадают. Верхнее основание цилиндра совпадает с сечением конуса плоскостью, параллельной основанию.

Осевое сечение цилиндра, вписанного в конус — представляет собой равнобедренный треугольник с вписанным в него прямоугольником.

NF=KM=h (l)— образующие цилиндра.

∆SOB∆KMB (по общему острому углу B)

, то есть: .

Отношение боковой поверхности конуса к боковой поверхности вписанного цилиндра (через радиусы основания и образующие)

, то есть .

В любой цилиндр можно вписать конус.

OS — ось цилиндра и ось конуса, высота цилиндра и конуса

OA — радиус конуса и радиус цилиндра

CA=DB=l — образующие цилиндра

∆SOA, ∆SCA, ∆SDB и ∆SOB — прямоугольные

∆SOA=∆SCA, ∆SDB = ∆SOB, поэтому 2S_∆ASB=2S_ACDB.

Отношение боковой поверхности конуса к боковой поверхности описанного около него цилиндра (через радиус основания и высоту)

, то есть .

2. Комбинация двух конусов

OS — ось конусов, высота большого конуса

OA — радиус большого конуса

В дне кашпо, имеющего форму конуса с площадью боковой поверхности 15π дм и радиусом основания 3 дм, сделано отверстие для того чтобы в него можно было вставить горшок для цветов, имеющий форму цилиндра. Определите радиус этого отверстия так, чтобы горшок для цветов был вписан в конус и имел форму равностороннего цилиндра.

AO=R – радиус основания конуса

Рассмотрим подобные треугольники AKC и AOS.

В них: .

OS=4 (из прямоугольного треугольника AOS с катетом 3 и гипотенузой 5.

KC=2r

Примеры и разбор решения заданий тренировочного модуля

1. В конус, осевым сечением которого является прямоугольный треугольник, вписан равносторонний цилиндр. Найдите отношение площадей полных поверхностей конуса и цилиндра.

Сделаем чертеж осевого сечения

Обозначим радиус цилиндра ЕО= r. Выразим через него все остальные элементы тел вращения.

Так как цилиндр равносторонний, то высота цилиндра равна h=СЕ=2r.

Так как сечение конуса ASB — прямоугольный треугольник и SO — его высота, то SO=OB. То есть высота конуса H равна радиусу R.

Образующая конуса равна L=SA=R .

∆SHD∆DKB∆OSB — прямоугольные равнобедренные треугольники.

Поэтому R=3r, образующая конуса равна SA=3r .

Выразим площади полных поверхностей конуса и цилиндра.

S_п.п.к. =πR(R+L)= π3r(3r+3r)=9πr 2 (1+ )

Теперь найдем отношение: .

Ответ: .

2. Усеченный конус вписан в цилиндр. Найдите площадь полной поверхности усеченного конуса, если радиус цилиндра равен 16, высота равна 6 а радиус меньшего основания усеченного конуса в два раза меньше радиуса цилиндра.

Сделаем чертеж осевого сечения:

O₁B — радиус меньшего основания усеченного конуса.

OC- радиус большего основания усеченного конуса и радиус цилиндра.

BH — высота цилиндра и высота усеченного конуса

По условию OC=2O₁B, ОС=16, BH=6.

Так как OC=2O₁B и ОС=16, то O₁B=8.

Рассмотрим треугольник BHC.

В нем HC=OC-OH=8, BH=6. По теореме Пифагора BC=10.

Теперь нам известен радиус меньшего основания усеченного конуса: он равен 8, радиус большего основания усеченного конуса: он равен 16, образующая усеченного конуса: она равна 10.

Найдем площадь боковой поверхности:

Площадь полной поверхности найдем, прибавив две площади оснований: