В цилиндр вписана четырехугольная призма у которой диагональ (8 видео)

Содержание

Объем цилиндра — урок 3 — КОНТРОЛЬНЫЕ И САМОСТОЯТЕЛЬНЫЕ РАБОТЫ
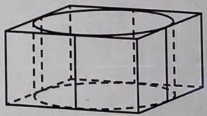
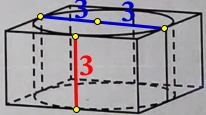
Решение №2305 Цилиндр вписан в правильную четырёхугольную призму. Радиус основания и высота цилиндра равны 3.
Объем цилиндра — урок 3 — КОНТРОЛЬНЫЕ И САМОСТОЯТЕЛЬНЫЕ РАБОТЫ
В цилиндр вписана правильная четырехугольная призма со стороной основания, равной 2, и диагональю равной √44. Найдите объем цилиндра, приняв π≈3
В цилиндр вписана четырехугольная призма у которой диагональ
Задача. Призма, вписанная в цилиндр
Задача. В цилиндр вписана правильная шестиугольная призма
💡 Видео

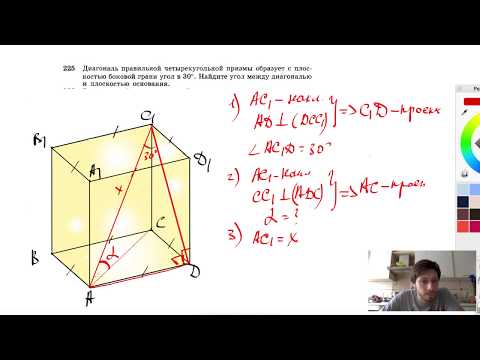
Видео:№225. Диагональ правильной четырехугольной призмы образует с плоскостью боковой грани угол в 30°.Скачать

Объем цилиндра — урок 3 — КОНТРОЛЬНЫЕ И САМОСТОЯТЕЛЬНЫЕ РАБОТЫ

Самостоятельная работа (20-25 мин.)

1. Основание прямой призмы — прямоугольный треугольник с катетом 6 см и острым углом 45°. Объем призмы равен 108 см3. Найдите площадь полной поверхности призмы.

2. Осевым сечением цилиндра является квадрат, диагональ которого равна 8√2 см. Найдите объем цилиндра. .

1. Основанием прямой призмы является ромб со стороной 12 см и углом 60°. Меньшее из диагональных сечений призмы является квадратом. Найдите объем призмы.

2. Осевым сечением цилиндра является квадрат, диагональ которого равна 6√2 см. Найдите объем цилиндра.

1. Основанием прямой призмы служит треугольник со сторонами 10, 10 и 12 см. Через большую сторону нижнего основания и середину противоположного бокового ребра проведена плоскость под углом 60° к плоскости основания. Найдите объем призмы.

2. Сечение цилиндра, параллельное его оси, отсекает от окружности основания дугу в 120°. Радиус основания цилиндра равен R, а угол между диагональю сечения и осью цилиндра равен 30°. Найдите объем цилиндра.

1. Основанием прямой призмы АВСА1В1С1 служит треугольник ABC, у которого АВ = ВС = 10, ∠ABC = 30°. Через ребро АА1 проведена плоскость, перпендикулярная грани СС1В1В. Диагональ сечения составляет с плоскостью основания угол в 45°. Найдите объем призмы.

2. Плоскость, параллельная оси цилиндра, проходит от нее на расстоянии 15 см. Диагональ получившегося сечения равна 20 см, а радиус основания цилиндра 17 см. Найдите объем цилиндра.

1. В основании прямой призмы лежит трапеция. Площади параллельных боковых граней призмы равны 8 см2 и 12 см2, а расстояние между ними равно 5 м. Найдите объем призмы.

2. В цилиндр вписана правильная четырехугольная призма, у которой диагональ равна α и образует с боковым ребром угол β. Найдите объем цилиндра.

1. В основании прямой призмы лежит трапеция. Объем призмы равен 40 см3. Площади параллельных боковых граней равны 6 см2 и 14 см2. Найдите расстояние между ними.

2. В цилиндр вписана правильная шестиугольная призма, большая диагональ которой равна l и образует с боковым ребром угол α. Найдите объем цилиндра.

Библиотека образовательных материалов для студентов, учителей, учеников и их родителей.

Наш сайт не претендует на авторство размещенных материалов. Мы только конвертируем в удобный формат материалы из сети Интернет, которые находятся в открытом доступе и присланные нашими посетителями.

Читайте также: Ремонт задних тормозных цилиндров калина

Если вы являетесь обладателем авторского права на любой размещенный у нас материал и намерены удалить его или получить ссылки на место коммерческого размещения материалов, обратитесь для согласования к администратору сайта.

Разрешается копировать материалы с обязательной гипертекстовой ссылкой на сайт, будьте благодарными мы затратили много усилий чтобы привести информацию в удобный вид.

Видео:Стереометрия. ЕГЭ. Правильная четырехугольная призма описана около цилиндра. Найдите высоту цилиндраСкачать

Решение №2305 Цилиндр вписан в правильную четырёхугольную призму. Радиус основания и высота цилиндра равны 3.

Цилиндр вписан в правильную четырёхугольную призму. Радиус основания и высота цилиндра равны 3. Найдите площадь боковой поверхности призмы.

Источник: Ященко ЕГЭ 2022 (36 вар)

Правильной четырёхугольной призмой – называется шестигранник, в основаниях которого находятся 2 квадрата, а боковые грани представлены прямоугольниками.
Площадь боковой поверхности данной призмы – это площадь 4-х равных прямоугольников.
Длина прямоугольника равна диаметру цилиндра, ширина прямоугольника равна высоте цилиндра.

Найдём площадь боковой поверхности призмы:

S_{бок. поверх.} = 4·S_{прямоугольника} = 4· h ·( r + r ) = 4·3·(3 + 3) = 4·3·6 = 72

Видео:Призма и цилиндр. Практическая часть. 11 класс.Скачать

Объем цилиндра — урок 3 — КОНТРОЛЬНЫЕ И САМОСТОЯТЕЛЬНЫЕ РАБОТЫ

Самостоятельная работа (20-25 мин.)

2. Осевым сечением цилиндра является квадрат, диагональ которого равна 8√2 см. Найдите объем цилиндра. .

2. Осевым сечением цилиндра является квадрат, диагональ которого равна 6√2 см. Найдите объем цилиндра.

Читайте также: Главный тормозной цилиндр для митсубиси паджеро спорт

Библиотека образовательных материалов для студентов, учителей, учеников и их родителей.

Видео:ЕГЭ математика СТЕРЕОМЕТРИЯ 8#5.18🔴Скачать

В цилиндр вписана правильная четырехугольная призма со стороной основания, равной 2, и диагональю равной √44. Найдите объем цилиндра, приняв π≈3

Диагональ основания равна 2√2.

Тогда высота и призмы и цилиндра равна Н:

Н = √((√44)² — (2√2)²) = √(44 -8) = √36 = 6 ед.

Радиус R основания цилиндра равен половине диагонали, то есть:

Площадь основания цилиндра So = πR² = 3*2 = 6 кв.ед.

Отсюда получаем ответ: V = SoH = 6*6 = 36 куб.ед.

1. Проводим луч b с началом в точке А перпендикулярно прямой ВС.
b∩BC = H.
На луче b по другую сторону от прямой ВС откладываем отрезок НА’ = AH.
Точка A’ построена.

2. Проводим луч МО. На этом луче за точку О откладываем отрезок ОМ₁= МО. Точка М₁ построена. М₁(- 4 ; 3)

3. Обозначим гипотенузу с, r — радиус вписанной окружности.
Для прямоугольного треугольника справедлива формула:
r = p — c, где р — его полупериметр.
p = r + c = 3 + 12 = 15 см

1. Проводим луч АС. На этом луче за точку С откладываем отрезок СА₁= АС. Точка А₁ построена.

2. Проводим луч с началом в точке D, перпендикулярно оси Ох. Пусть он пересечет ос Ох в точке Н. На это луче за точку Н откладываем отрезок HD₁ = DH. Точка D₁ построена. D₁(- 3 ; — 2).

3. Центральный угол в два раза больше вписанного, опирающегося на ту же дугу.
Пусть вписанный ∠АСВ = х, тогда ∠АОВ = 2х.
2x — x = 50
x = 50
∠АСВ = 50°
∠АОВ = 100°

Видео:Цилиндр вписан в четырехугольную призму. Найдите площадь боковой поверхности призмы.Скачать

В цилиндр вписана четырехугольная призма у которой диагональ

Примечание. Это часть урока с задачами по геометрии (раздел стереометрия). Если Вам необходимо решить задачу по геометрии, которой здесь нет — пишите об этом в форуме. В задачах вместо символа «квадратный корень» применяется функция sqrt(), в которой sqrt — символ квадратного корня, а в скобках указано подкоренное выражение.

Видео:ВПИСАННАЯ И ОПИСАННАЯ ПРИЗМЫ // СТЕРЕОМЕТРИЯСкачать

Задача. Призма, вписанная в цилиндр

В цилиндр вписана призма. Основанием призмы служит прямоугольный треугольник, катет которого равен 2а, а прилежащий угол равен 60 градусам. Диагональ большей боковой грани призмы составляет с плоскостью ее основания угол в 45 градусов. Найдите объем цилиндра.

Решение .
Объем цилиндра найдем по формуле:

где:
R — радиус основания прямого цилиндра,
h — высота.

Найдем основание цилиндра. 1-й способ .
Основание цилиндра одновременно является окружностью, описанной вокруг прямоугольного треугольника, являющегося основанием призмы. Диаметр окружности, описанной вокруг прямоугольного треугольника, лежит на его гипотенузе. То есть длина гипотенузы равна 2R.

Радиус окружности, описанной вокруг треугольника найдем по формуле:

R = x / 2 sin α
где:
x — сторона треугольника
α — угол, противолежащий стороне а.

Противолежащий угол найдем следующим образом. Поскольку треугольник прямоугольный, то противолежащий катету угол будет равен 180-90-60 = 30 градусов. Таким образом, радиус описанной окружности (он же радиус цилиндра) равен:

Найдем основание цилиндра. 2-й способ
У прямоугольного треугольника гипотенуза одновременно является диаметром описанной окружности. Половина гипотенузы будет равна ее радиусу.
Таким образом найдем гипотенузу для прямоугольного треугольника, зная угол и его катет через тригонометрическую функцию:
2R = 2a / cos 60 = 2a / 0.5 = 4a
R = 2a

Найдем высоту цилиндра .
Диаметр описанной окружности образует с диагональю призмы прямоугольный треугольник, один катет которого является диаметром описанной окружности, второй — высотой цилиндра и призмы, а гипотенуза является диагональю большей стороны призмы и одновременно цилиндра.

Поскольку угол диагонали с основанием составляет 45 градусов, то второй угол равен 180 — 45 — 90 = 45 градусов.
Исходя из того, что прямоугольный треугольник равнобедренный, то высота цилиндра и призмы равна диаметру окружности. Таким образом:

V = пR 2 h
V = п*4a 2 *4a
V = п16a 3 .

Видео:ЕГЭ 2022 математика задача 4 вариант 2Скачать

Задача. В цилиндр вписана правильная шестиугольная призма

В цилиндр вписана правильная шестиугольная призма. Найти угол между диагональю ее боковой грани и осью цилиндра, если радиус основания равен высоте цилиндра.

Если радиус основания равен высоте цилиндра, диагональ боковой грани правильной шестиугольной призмы представляет собой прямоугольный треугольник, у которого один из катетов равен высоте цилиндра (r), а второй катет равен стороне шестиугольника, вписанного в окружность.Согласно свойствам шестиугольника, вписанного в окружность, его сторона равна радиусу такой окружности.

То есть, каждая боковая грань данной вписанной призмы – квадрат. Диагональ грани образует с осью цилиндра, как и с боковым ребром, одинаковый угол 45°, так как ось цилиндра и боковые ребра вписанной призмы параллельны.