- Решение №2305 Цилиндр вписан в правильную четырёхугольную призму. Радиус основания и высота цилиндра равны 3.
- В цилиндр вписана правильная шестиугольная призма найдите площадь боковой поверхности
- Решение №2305 Цилиндр вписан в правильную четырёхугольную призму. Радиус основания и высота цилиндра равны 3.
- В цилиндр вписана правильная шестиугольная призма найдите площадь боковой поверхности
- Найдите площадь боковой поверхности правильной
- 🔥 Видео
Видео:Стереометрия. ЕГЭ. Площадь боковой поверхности правильной шестиугольной призмыСкачать

Решение №2305 Цилиндр вписан в правильную четырёхугольную призму. Радиус основания и высота цилиндра равны 3.
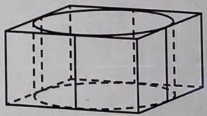
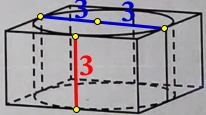
Цилиндр вписан в правильную четырёхугольную призму. Радиус основания и высота цилиндра равны 3. Найдите площадь боковой поверхности призмы.
Источник: Ященко ЕГЭ 2022 (36 вар)
Правильной четырёхугольной призмой – называется шестигранник, в основаниях которого находятся 2 квадрата, а боковые грани представлены прямоугольниками.
Площадь боковой поверхности данной призмы – это площадь 4-х равных прямоугольников.
Длина прямоугольника равна диаметру цилиндра, ширина прямоугольника равна высоте цилиндра.
Найдём площадь боковой поверхности призмы:
Sбок. поверх. = 4·Sпрямоугольника = 4· h ·( r + r ) = 4·3·(3 + 3) = 4·3·6 = 72
Видео:ЕГЭ Задание 8 Правильная шестиугольная призмаСкачать

В цилиндр вписана правильная шестиугольная призма найдите площадь боковой поверхности
Шар вписан в цилиндр. Площадь полной поверхности цилиндра равна 18. Найдите площадь поверхности шара.
Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 1. Найдите объем параллелепипеда.
Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 4. Объем параллелепипеда равен 16. Найдите высоту цилиндра.
В куб вписан шар радиуса 1. Найдите объем куба.
В основании прямой призмы лежит прямоугольный треугольник с катетами 6 и 8. Боковые ребра равны Найдите объем цилиндра, описанного около этой призмы.
В основании прямой призмы лежит квадрат со стороной 2. Боковые ребра равны Найдите объем цилиндра, описанного около этой призмы.
Цилиндр и конус имеют общие основание и высоту. Объём конуса равен 25. Найдите объём цилиндра.
Из единичного куба вырезана правильная четырехугольная призма со стороной основания 0,5 и боковым ребром 1. Найдите площадь поверхности оставшейся части куба.
Цилиндр и конус имеют общие основание и высоту. Найдите объем конуса, если объем цилиндра равен 150.
Объём куба, описанного около сферы, равен 216. Найдите радиус сферы.
Конус описан около правильной четырехугольной пирамиды со стороной основания 4 и высотой 6. Найдите его объем, деленный на
Во сколько раз объем конуса, описанного около правильной четырехугольной пирамиды, больше объема конуса, вписанного в эту пирамиду?
В куб с ребром 3 вписан шар. Найдите объем этого шара, деленный на
Читайте также: Правильная четырехугольная призма описана около цилиндра найдите объем цилиндра
Около куба с ребром описан шар. Найдите объем этого шара, деленный на
Вершина A куба с ребром 1,6 является центром сферы, проходящей через точку A1. Найдите площадь S части сферы, содержащейся внутри куба. В ответе запишите величину
Видео:ЕГЭ 2022 математика задача 4 вариант 2Скачать

Решение №2305 Цилиндр вписан в правильную четырёхугольную призму. Радиус основания и высота цилиндра равны 3.
Цилиндр вписан в правильную четырёхугольную призму. Радиус основания и высота цилиндра равны 3. Найдите площадь боковой поверхности призмы.
Источник: Ященко ЕГЭ 2022 (36 вар)
Правильной четырёхугольной призмой – называется шестигранник, в основаниях которого находятся 2 квадрата, а боковые грани представлены прямоугольниками.
Площадь боковой поверхности данной призмы – это площадь 4-х равных прямоугольников.
Длина прямоугольника равна диаметру цилиндра, ширина прямоугольника равна высоте цилиндра.
Найдём площадь боковой поверхности призмы:
Sбок. поверх. = 4·Sпрямоугольника = 4· h ·( r + r ) = 4·3·(3 + 3) = 4·3·6 = 72
Видео:ЕГЭ. Задача 8. Призма и цилиндрСкачать

В цилиндр вписана правильная шестиугольная призма найдите площадь боковой поверхности
Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны 1. Найдите площадь боковой поверхности призмы.
Высота призмы равна высоте цилиндра, а сторона ее основания равна диаметру цилиндра. Боковые грани призмы — прямоугольники со сторонами 1 и 2. Поэтому площадь боковой поверхности 4 · 1 · 2 = 8.
Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны 16. Найдите площадь боковой поверхности призмы.
Это задание ещё не решено, приводим решение прототипа.
Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны 1. Найдите площадь боковой поверхности призмы.
Высота призмы равна высоте цилиндра, а сторона ее основания равна диаметру цилиндра. Боковые грани призмы — прямоугольники со сторонами 1 и 2. Поэтому площадь боковой поверхности 4 · 1 · 2 = 8.
Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны 1. Найдите площадь боковой поверхности призмы.
Это задание ещё не решено, приводим решение прототипа.
Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны 1. Найдите площадь боковой поверхности призмы.
Высота призмы равна высоте цилиндра, а сторона ее основания равна диаметру цилиндра. Боковые грани призмы — прямоугольники со сторонами 1 и 2. Поэтому площадь боковой поверхности 4 · 1 · 2 = 8.
Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны 7. Найдите площадь боковой поверхности призмы.
Это задание ещё не решено, приводим решение прототипа.
Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны 1. Найдите площадь боковой поверхности призмы.
Читайте также: Передние тормозные цилиндры ваз классика
Высота призмы равна высоте цилиндра, а сторона ее основания равна диаметру цилиндра. Боковые грани призмы — прямоугольники со сторонами 1 и 2. Поэтому площадь боковой поверхности 4 · 1 · 2 = 8.
Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны 5,5. Найдите площадь боковой поверхности призмы.
Это задание ещё не решено, приводим решение прототипа.
Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны 1. Найдите площадь боковой поверхности призмы.
Высота призмы равна высоте цилиндра, а сторона ее основания равна диаметру цилиндра. Боковые грани призмы — прямоугольники со сторонами 1 и 2. Поэтому площадь боковой поверхности 4 · 1 · 2 = 8.
Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны 9. Найдите площадь боковой поверхности призмы.
Это задание ещё не решено, приводим решение прототипа.
Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны 1. Найдите площадь боковой поверхности призмы.
Высота призмы равна высоте цилиндра, а сторона ее основания равна диаметру цилиндра. Боковые грани призмы — прямоугольники со сторонами 1 и 2. Поэтому площадь боковой поверхности 4 · 1 · 2 = 8.
Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны 17. Найдите площадь боковой поверхности призмы.
Это задание ещё не решено, приводим решение прототипа.
Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны 1. Найдите площадь боковой поверхности призмы.
Высота призмы равна высоте цилиндра, а сторона ее основания равна диаметру цилиндра. Боковые грани призмы — прямоугольники со сторонами 1 и 2. Поэтому площадь боковой поверхности 4 · 1 · 2 = 8.
Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны 14. Найдите площадь боковой поверхности призмы.
Это задание ещё не решено, приводим решение прототипа.
Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны 1. Найдите площадь боковой поверхности призмы.
Высота призмы равна высоте цилиндра, а сторона ее основания равна диаметру цилиндра. Боковые грани призмы — прямоугольники со сторонами 1 и 2. Поэтому площадь боковой поверхности 4 · 1 · 2 = 8.
Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны 4. Найдите площадь боковой поверхности призмы.
Это задание ещё не решено, приводим решение прототипа.
Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны 1. Найдите площадь боковой поверхности призмы.
Читайте также: Не работает 2 цилиндр калина 8кл
Высота призмы равна высоте цилиндра, а сторона ее основания равна диаметру цилиндра. Боковые грани призмы — прямоугольники со сторонами 1 и 2. Поэтому площадь боковой поверхности 4 · 1 · 2 = 8.
Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны 23,5. Найдите площадь боковой поверхности призмы.
Это задание ещё не решено, приводим решение прототипа.
Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны 1. Найдите площадь боковой поверхности призмы.
Высота призмы равна высоте цилиндра, а сторона ее основания равна диаметру цилиндра. Боковые грани призмы — прямоугольники со сторонами 1 и 2. Поэтому площадь боковой поверхности 4 · 1 · 2 = 8.
Видео:Цилиндр вписан в четырехугольную призму. Найдите площадь боковой поверхности призмы.Скачать

Найдите площадь боковой поверхности правильной
27065. Найдите площадь боковой поверхности правильной треугольной призмы, описанной около цилиндра, радиус основания которого равен √3, а высота равна 2.
Площадь боковой поверхности данной призмы равна сумме площадей всех боковых граней. Так как дана правильная треугольная призма, то все три грани являются прямоугольниками, площади которых равны.
Для нахождения площади боковой грани необходимо знать её высоту и длину ребра основания. Высота дана. Найдём длину ребра основания. Рассмотрим проекцию (вид сверху:
Из прямоугольного треугольника АОС можем найти АС. По определению тангенса: Значит
Таким образом, сторона правильного треугольника выражается через радиус вписанной в него окружности как Значит площадь боковой поверхности будет равна: Ответ: 36
27066. Найдите площадь боковой поверхности правильной шестиугольной призмы, описанной около цилиндра, радиус основания которого равен √3, а высота равна 2.
Площадь боковой поверхности призмы равна произведению периметра снования и высоты. *Высота призмы равна высоте цилиндра. Вычислим сторону шестиугольника. Построим эскиз: Треугольник AOH равносторонний, Провели высоту OH, АН=НВ. Можем записать: Следовательно АВ=2. Таким образом, периметр шестиугольника равен 12, а искомая площадь 24 (периметр умножили на высоту призмы).
27107. Найдите площадь боковой поверхности правильной треугольной призмы, вписанной в цилиндр, радиус основания которого равен 2√3, а высота равна 2.
Площадь боковой поверхности призмы равна: Сторона правильного треугольника выражается через радиус описанной окружности как: Тогда площадь боковой поверхности призмы равна: Ответ: 36
27064. Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны 1. Найдите площадь боковой поверхности призмы.
Диаметр цилиндра равен стороне квадрата лежащего в основании, это 2. Тогда периметр квадрата равен 8. Площадь боковой поверхности равна 8∙1=8.
🔥 Видео
Стереометрия. ЕГЭ. Найдите площадь боковой поверхности правильной шестиугольной призмыСкачать

Правильная шестиугольная призмаСкачать

#113. Задание 8: шестиугольная призмаСкачать

🔴 Стороны основания правильной шестиугольной ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 16 | ШКОЛА ПИФАГОРАСкачать

Стереометрия. ЕГЭ. Правильная четырехугольная призма описана около цилиндраСкачать

Площадь поверхности призмы. 11 класс.Скачать

Нахождение площади боковой поверхности цилиндраСкачать

Правильная шестиугольная призма Угол между прямымиСкачать
ЕГЭ по математике. Профильный уровень. Задание 8. Правильная шестиугольная призма. УголСкачать

ЦИЛИНДР | 9 класс геометрия Атанасян | задачи 1215 1217Скачать

#130. Задание 8: комбинация телСкачать

ЕГЭ. Математика. База . Задача 16. Дана Правильная шестиугольная призма все ребра которой равны 1Скачать

Стереометрия. ЕГЭ. Правильная четырехугольная призма описана около цилиндра. Найдите высоту цилиндраСкачать