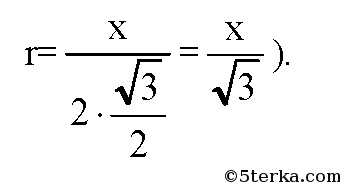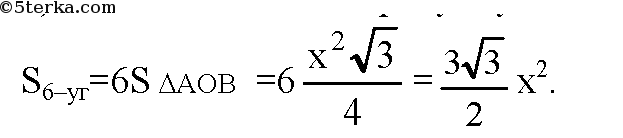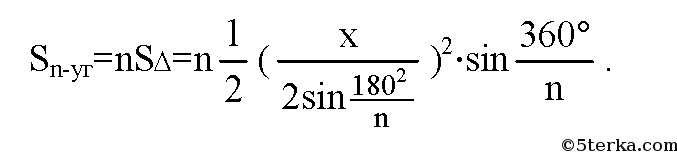- Призмы, вписанные в цилиндр. Свойства призмы, вписанной в цилиндр
- 671. В цилиндр вписана правильная n-угольная призма. Найдите отношение объемов призмы и цилиндра, если: а) n = 3; б) n = 4; в) n=6; г) n = 8; д) n произвольное целое число.
- Цилиндры, вписанные в призмы
- Цилиндры, вписанные в призмы. Свойства призмы, описанной около цилиндра
- Отношение объемов цилиндра и описанной около него правильной n — угольной призмы
- В цилиндр вписана правильная треугольная призма а в нее цилиндр
- Задача. Призма, вписанная в цилиндр
- Задача. В цилиндр вписана правильная шестиугольная призма
- 🎦 Видео
Видео:11 класс. Контрольная №4 (из 6). Тема: Объем призмы, цилиндра и конуса. Решение с советами! :)Скачать

Призмы, вписанные в цилиндр. Свойства призмы, вписанной в цилиндр
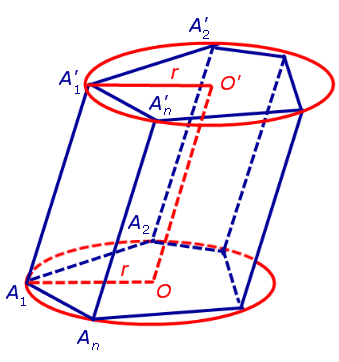
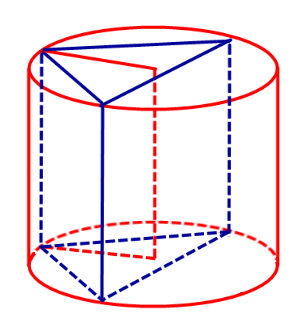
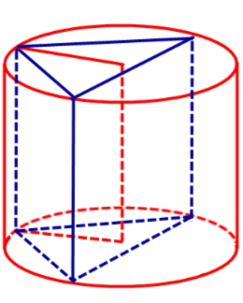
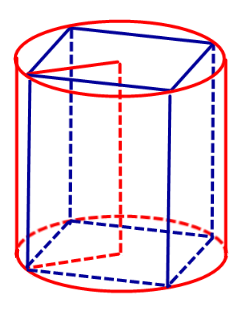
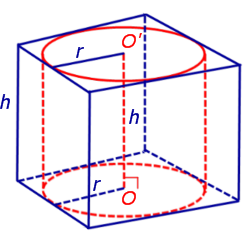
Определение 1. Призмой, вписанной в цилиндр, называют такую призму, основания которой вписаны в окружности оснований цилиндра, а боковые ребра призмы являются образующими цилиндра (рис. 1).
Определение 2. Если призма вписана в цилиндр, то цилиндр называют описанным около призмы.
Прежде, чем перейти к вопросу о том, какую призму можно вписать в цилиндр, докажем следующее свойство призм.
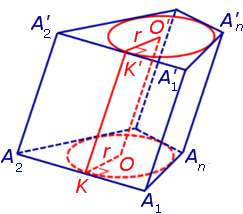
Утверждение 1. Если около оснований призмы можно описать окружности, то отрезок, соединяющий центры описанных окружностей, будет параллелелен и равен боковому ребру призмы.
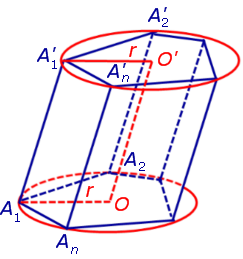
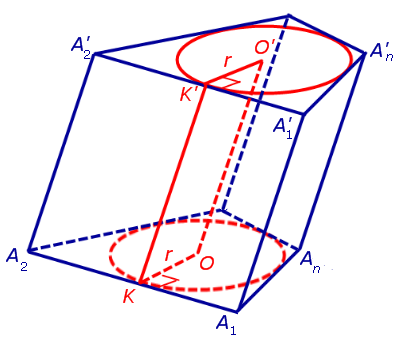
Докажем, что точка O’ является центром окружности радиуса r, описанной около верхнего основания призмы. С этой целью рассмотрим, например, четырехугольник A1A’1O’O (рис. 2).
Рассуждая аналогичным образом, заключаем, что
то есть точка O’ – центр окружности радиуса r , описанной около верхнего основания призмы.
В силу того, что четырехугольник OO’A1A’1 является параллелограммом, получаем равенство
Теорема. Около призмы можно описать цилиндр тогда и только тогда, когда выполнены следующие два условия:
- Призма является прямой призмой;
- Около оснований призмы можно описать окружности.
Доказательство. Докажем сначала, что если около n – угольной призмы описан цилиндр, то оба условия теоремы выполнены.
Действительно, выполнение условия 2 следует непосредственно из определения цилиндра, описанного около призмы. Из этого определения также следует, что вписанная в цилиндр призма является прямой призмой, поскольку образующие цилиндра перпендикулярны к плоскостям его оснований,
Таким образом, мы доказали, что, если призма вписана в цилиндр, то оба условия теоремы выполнены.
Теперь рассмотрим прямую n – угольную призму высоты h, около оснований которой можно описать окружности, и докажем, что около такой призмы можно описать цилиндр.
Обозначим буквой O центр окружности радиуса r, описанной около нижнего основания призмы, а символом O’ обозначим центр окружности, описанной около верхнего основания призмы.
Поскольку многоугольники, лежащие в основаниях призмы равны, то и радиусы описанных около них окружностей будут равны. Согласно утверждению 1 отрезок OO’ параллелен и равен боковому ребру призмы. Так как рассматриваемая призма прямая, то ее боковые ребра перпендикулярны плоскости основания и равны высоте призмы h. Значит, и отрезок OO’ перпендикулярен плоскости основания призмы и равен h.
Читайте также: Как поршень уплотняется внутри цилиндра
Цилиндр с осью OO’ , радиусом r и высотой h и будет описан около исходной призмы.
Доказательство теоремы завершено.
Следствие 1. Высота призмы, вписанной в цилиндр, равна высоте цилиндра.
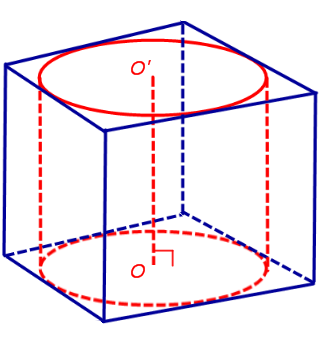
Следствие 2. Около любой прямой треугольной призмы можно описать цилиндр (рис. 4).
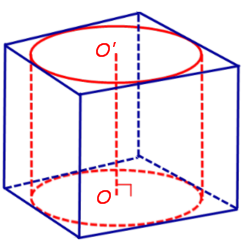
Следствие 3. Около любого прямоугольного параллелепипеда (в частности, около куба прямоугольного параллелепипеда (в частности, около куба ) можно описать цилиндр (рис. 5).
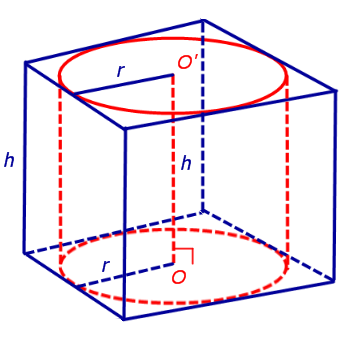
Замечание 1. Если у прямоугольного параллелепипеда прямоугольного параллелепипеда три ребра, выходящие из одной вершины, равны a, b, c и различны, то существует три возможности описать около этого параллелепипеда цилиндр в зависимости от того, какое из ребер параллелепипеда выбрано в качестве образующей описанного цилиндра (рис. 6, 7, 8).
Видео:xi408 Комбинации с цилиндромСкачать

671. В цилиндр вписана правильная n-угольная призма. Найдите отношение объемов призмы и цилиндра, если: а) n = 3; б) n = 4; в) n=6; г) n = 8; д) n произвольное целое число.
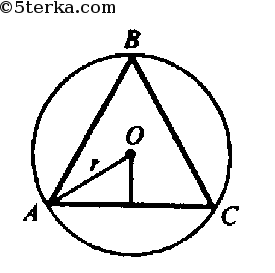
а) n=3, ΔАВС — правильный. Обозначим сторону ΔАВС равной х, следовательно,

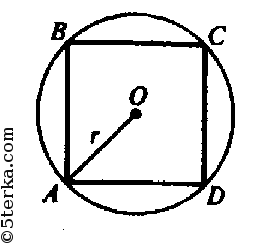
б) n=4, ABCD — квадрат. Обозначим сторону квадрата равной х.
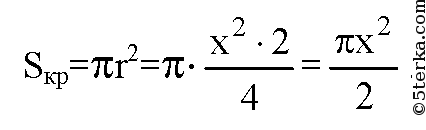
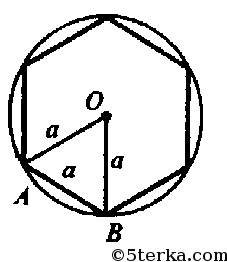
в) n=6. Обозначим сторону 6-угольника за х, следовательно, r=х.
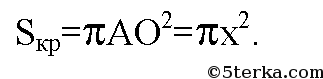
г) обозначим сторону правильного вписанного n-угольника за х. Следовательно, радиус описанной окружности равен
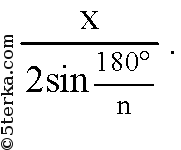
(Правильный n-угольник разбивается радиусами, проведенными из центра, на n одинаковых треугольников; все треугольники равновелики)
Решебник по геометрии за 10 класс (Л.С.Атанасян, 2001 год),
задача №671
к главе «Глава VII. Объемы тел. § 2. Объём прямой призмы и цилиндра».
Видео:ЕГЭ 2017 по Математике. Призма вписана в цилиндр Задание 8 #4Скачать

Цилиндры, вписанные в призмы
Видео:Призма, вписанная в цилиндр.The prism inscribed in the cylinder.Скачать

Цилиндры, вписанные в призмы. Свойства призмы, описанной около цилиндра
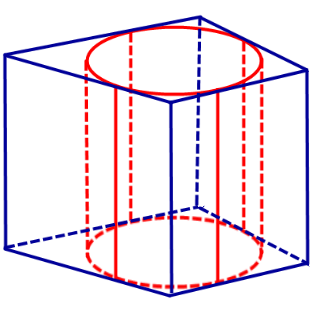
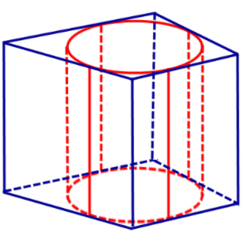
Определение 2. Если цилиндр вписан в призму, то призму называют описанной около цилиндра.
Прежде, чем перейти к вопросу о том, в какую же призму можно вписать цилиндр, докажем следующее свойство призм.
Утверждение 1. Если в основания призмы можно вписать окружности, то отрезок, соединяющий центры вписанных окружностей, будет параллелелен и равен боковому ребру призмы.
Рассуждая аналогичным образом, заключаем, что точка O’ равноудалена от всех прямых, на которых лежат ребра верхнего основания A’1A’2, A’2A’3, . , An – 1An , а поскольку O’ лежит в плоскости верхнего основания, то точка O’ является центром вписанной в многоугольник A’1A’2 . A’n окружности.
В силу того, что прямые OO’ и A1A’1 параллельны по построению, а прямые OA1 и O’A’ параллельны как линии пересечения двух параллельных плоскостей третьей плоскостью, замечаем, что четырехугольник OO’A1A’1 является параллелограммом, откуда вытекает равенство: OO’ = A1A’1 .
Теорема. В призму можно вписать цилиндр тогда и только тогда, когда выполнены следующие два условия:
- Призма является прямой призмой;
- В основания призмы можно вписать окружности.
Доказательство. Докажем сначала, что если в n – угольную призму вписан цилиндр, то оба условия теоремы выполнены.
Действительно, выполнение условия 2 следует непосредственно из определения цилиндра, вписанного в призму. Докажем, что выполняется и условие 1, т.е. докажем, что описанная около цилиндра призма является прямой призмой.
Читайте также: Расположение цилиндров зил бычок
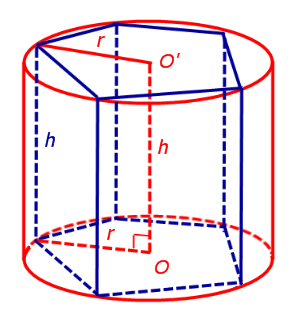
С этой целью рассмотрим ось цилиндра OO’ , соединяющую центры окружностей, вписанных в нижнее и верхнее основания призмы (рис. 3).
Согласно утверждению 1 отрезок OO’ параллелен боковым ребрам призмы. Поскольку ось цилиндра OO’ перпендикулярна к плоскостям его оснований, то и боковые ребра призмы также перпендикулярны к плоскостям оснований, то есть призма является прямой призмой.
Таким образом, мы доказали, что, если призма описана около цилиндра, то оба условия теоремы выполнены.
Теперь рассмотрим прямую n – угольную призму высоты h, в основания которой можно вписать окружности, и докажем, что в такую призму можно вписать цилиндр.
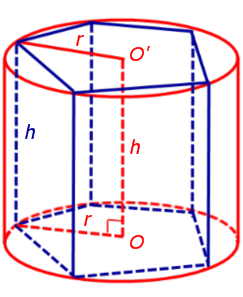
Обозначим буквой O центр окружности радиуса r, вписанной в нижнее основание призмы, а символом O’ обозначим центр окружности, вписанной в верхнее основание призмы (рис. 4).
Поскольку многоугольники, лежащие в основаниях призмы равны, то и радиусы вписанных в них окружностей будут равны. Согласно утверждению 1 отрезок OO’ параллелен и равен боковому ребру призмы. Так как рассматриваемая призма прямая, то ее боковые ребра перпендикулярны плоскости основания и равны высоте призмы h. Значит, и отрезок OO’ перпендикулярен плоскости основания призмы и равен h.
Цилиндр с осью OO’ , радиусом r и высотой h и будет вписан в исходную призму.
Доказательство теоремы завершено.
Следствие 1 . Высота призмы, описанной около цилиндра, равна высоте цилиндра.
Следствие 2. В любую прямую треугольную призму можно вписать цилиндр.
Справедливость этого утверждения вытекает из того факта, что в любой треугольник можно вписать окружность.
Следствие 3. В любую правильную n – угольную призму можно вписать цилиндр.
Для доказательства этого следствия достаточно заметить, правильная призма является прямой призмой. Основаниями правильной призмы являются правильные многоугольники, а в любой правильный n – угольник можно вписать окружность.
Видео:11 класс. Геометрия. Объем цилиндра. 14.04.2020Скачать

Отношение объемов цилиндра и описанной около него правильной n — угольной призмы
Задача. Найти отношение объемов цилиндра и описанной около него правильной n — угольной призмы.
Решение. Поскольку и объем цилиндра, и объем призмы объем призмы вычисляются по формуле
а высота цилиндра равна высоте описанной около него призмы, то для объемов цилиндра и описанной около него правильной n — угольной призмы справедливо равенство
Следствие 4. Отношение объема цилиндра к объему описанной около него правильной треугольной призмы правильной треугольной призмы равно
Следствие 5. Отношение объема цилиндра к объему описанной около него правильной четырехугольной призмы правильной четырехугольной призмы равно
Следствие 6. Отношение объема цилиндра к объему описанной около него правильной шестиугольной призмы равно
Видео:Призма и цилиндр. Практическая часть. 11 класс.Скачать

В цилиндр вписана правильная треугольная призма а в нее цилиндр
Примечание. Это часть урока с задачами по геометрии (раздел стереометрия). Если Вам необходимо решить задачу по геометрии, которой здесь нет — пишите об этом в форуме. В задачах вместо символа «квадратный корень» применяется функция sqrt(), в которой sqrt — символ квадратного корня, а в скобках указано подкоренное выражение.
Видео:Треугольная призма. Ортогональные и изометрическая проекции. Урок 10.(Часть2. ПРОЕКЦИОННОЕ ЧЕРЧЕНИЕ)Скачать

Задача. Призма, вписанная в цилиндр
В цилиндр вписана призма. Основанием призмы служит прямоугольный треугольник, катет которого равен 2а, а прилежащий угол равен 60 градусам. Диагональ большей боковой грани призмы составляет с плоскостью ее основания угол в 45 градусов. Найдите объем цилиндра.
Решение .
Объем цилиндра найдем по формуле:
где:
R — радиус основания прямого цилиндра,
h — высота.
Найдем основание цилиндра. 1-й способ .
Основание цилиндра одновременно является окружностью, описанной вокруг прямоугольного треугольника, являющегося основанием призмы. Диаметр окружности, описанной вокруг прямоугольного треугольника, лежит на его гипотенузе. То есть длина гипотенузы равна 2R.
Радиус окружности, описанной вокруг треугольника найдем по формуле:
R = x / 2 sin α
где:
x — сторона треугольника
α — угол, противолежащий стороне а.
Противолежащий угол найдем следующим образом. Поскольку треугольник прямоугольный, то противолежащий катету угол будет равен 180-90-60 = 30 градусов. Таким образом, радиус описанной окружности (он же радиус цилиндра) равен:
Найдем основание цилиндра. 2-й способ
У прямоугольного треугольника гипотенуза одновременно является диаметром описанной окружности. Половина гипотенузы будет равна ее радиусу.
Таким образом найдем гипотенузу для прямоугольного треугольника, зная угол и его катет через тригонометрическую функцию:
2R = 2a / cos 60 = 2a / 0.5 = 4a
R = 2a
Найдем высоту цилиндра .
Диаметр описанной окружности образует с диагональю призмы прямоугольный треугольник, один катет которого является диаметром описанной окружности, второй — высотой цилиндра и призмы, а гипотенуза является диагональю большей стороны призмы и одновременно цилиндра.
Поскольку угол диагонали с основанием составляет 45 градусов, то второй угол равен 180 — 45 — 90 = 45 градусов.
Исходя из того, что прямоугольный треугольник равнобедренный, то высота цилиндра и призмы равна диаметру окружности. Таким образом:
V = пR 2 h
V = п*4a 2 *4a
V = п16a 3 .
Видео:Стереометрия. ЕГЭ. Правильная четырехугольная призма описана около цилиндра. Найдите высоту цилиндраСкачать

Задача. В цилиндр вписана правильная шестиугольная призма
В цилиндр вписана правильная шестиугольная призма. Найти угол между диагональю ее боковой грани и осью цилиндра, если радиус основания равен высоте цилиндра.
Если радиус основания равен высоте цилиндра, диагональ боковой грани правильной шестиугольной призмы представляет собой прямоугольный треугольник, у которого один из катетов равен высоте цилиндра (r), а второй катет равен стороне шестиугольника, вписанного в окружность.Согласно свойствам шестиугольника, вписанного в окружность, его сторона равна радиусу такой окружности.
То есть, каждая боковая грань данной вписанной призмы – квадрат. Диагональ грани образует с осью цилиндра, как и с боковым ребром, одинаковый угол 45°, так как ось цилиндра и боковые ребра вписанной призмы параллельны.
🎦 Видео
№ 1215 - Геометрия 7-9 класс АтанасянСкачать

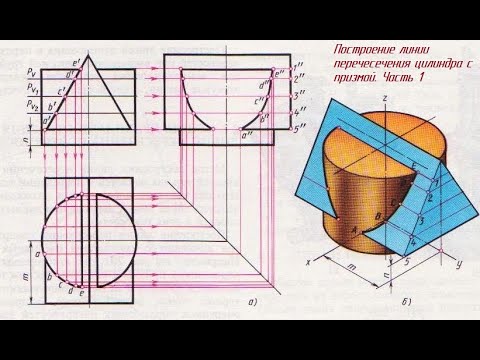
Задание 54. Чертеж ЛИНИИ ПЕРЕСЕЧЕНИЯ цилиндра и призмы трехгранной Часть 1Скачать
ЕГЭ. Задача 8. Призма и цилиндрСкачать

ВПИСАННАЯ И ОПИСАННАЯ ПРИЗМЫ // СТЕРЕОМЕТРИЯСкачать

Правильная треугольная призмаСкачать

Призма, описанная около шара, или шар, вписанный в призму.Скачать

#130. Задание 8: комбинация телСкачать

xi604 Объем цилиндраСкачать

Объём цилиндраСкачать

Геометрия Правильная треугольная призма вписана в шар. Найдите высоту призмы если радиус шараСкачать

ЕГЭ СТЕРЕОМЕТРИЯ В ЦИЛИНДР ВПИСАНА ПРИЗМА СОВМЕЩЕННЫЕ ФИГУРЫ НА ЕГЭ | ВПИСАННЫЕ ОКРУЖНОСТИ ГЛОБАЛКАСкачать

Геометрия 3D § 10 - Геометрия 9 класс КазаковСкачать