В цилиндр вписана правильная треугольная призма а в призму вписан (8 видео)

Содержание

Цилиндры, вписанные в призмы. Свойства призмы, описанной около цилиндра
Отношение объемов цилиндра и описанной около него правильной n — угольной призмы
Тема урока «Призма, вписанная в цилиндр. Цилиндр, вписанный в призму»
📽️ Видео

Видео:07 Стереометрия на ЕГЭ по математике. Призма вписана в цилиндр.Скачать

Цилиндры, вписанные в призмы. Свойства призмы, описанной около цилиндра

Определение 2. Если цилиндр вписан в призму, то призму называют описанной около цилиндра.

Прежде, чем перейти к вопросу о том, в какую же призму можно вписать цилиндр, докажем следующее свойство призм.

Утверждение 1. Если в основания призмы можно вписать окружности, то отрезок, соединяющий центры вписанных окружностей, будет параллелелен и равен боковому ребру призмы.

Рассуждая аналогичным образом, заключаем, что точка O’ равноудалена от всех прямых, на которых лежат ребра верхнего основания A’₁A’₂, A’₂A’₃, . , A_{n – 1}A_n , а поскольку O’ лежит в плоскости верхнего основания, то точка O’ является центром вписанной в многоугольник A’₁A’₂ . A’_n окружности.

В силу того, что прямые OO’ и A₁A’₁ параллельны по построению, а прямые OA₁ и O’A’ параллельны как линии пересечения двух параллельных плоскостей третьей плоскостью, замечаем, что четырехугольник OO’A₁A’₁ является параллелограммом, откуда вытекает равенство: OO’ = A₁A’₁ .

Теорема. В призму можно вписать цилиндр тогда и только тогда, когда выполнены следующие два условия:

Призма является прямой призмой;
В основания призмы можно вписать окружности.

Доказательство. Докажем сначала, что если в n – угольную призму вписан цилиндр, то оба условия теоремы выполнены.

Действительно, выполнение условия 2 следует непосредственно из определения цилиндра, вписанного в призму. Докажем, что выполняется и условие 1, т.е. докажем, что описанная около цилиндра призма является прямой призмой.

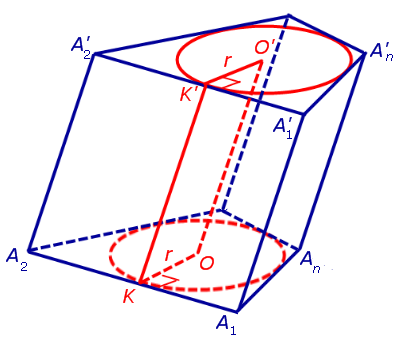
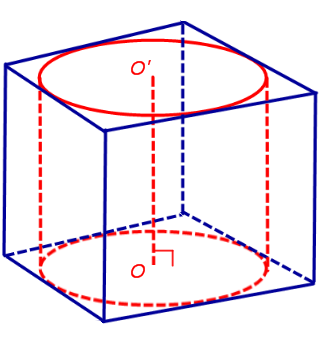
С этой целью рассмотрим ось цилиндра OO’ , соединяющую центры окружностей, вписанных в нижнее и верхнее основания призмы (рис. 3).

Согласно утверждению 1 отрезок OO’ параллелен боковым ребрам призмы. Поскольку ось цилиндра OO’ перпендикулярна к плоскостям его оснований, то и боковые ребра призмы также перпендикулярны к плоскостям оснований, то есть призма является прямой призмой.

Таким образом, мы доказали, что, если призма описана около цилиндра, то оба условия теоремы выполнены.

Теперь рассмотрим прямую n – угольную призму высоты h, в основания которой можно вписать окружности, и докажем, что в такую призму можно вписать цилиндр.

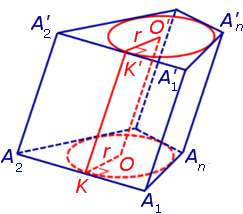
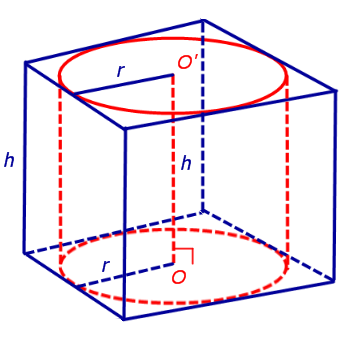
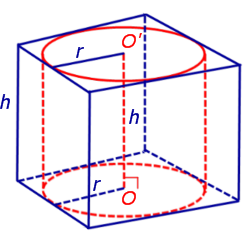
Обозначим буквой O центр окружности радиуса r, вписанной в нижнее основание призмы, а символом O’ обозначим центр окружности, вписанной в верхнее основание призмы (рис. 4).

Поскольку многоугольники, лежащие в основаниях призмы равны, то и радиусы вписанных в них окружностей будут равны. Согласно утверждению 1 отрезок OO’ параллелен и равен боковому ребру призмы. Так как рассматриваемая призма прямая, то ее боковые ребра перпендикулярны плоскости основания и равны высоте призмы h. Значит, и отрезок OO’ перпендикулярен плоскости основания призмы и равен h.

Читайте также: Диаметр цилиндра ybr 125

Цилиндр с осью OO’ , радиусом r и высотой h и будет вписан в исходную призму.

Доказательство теоремы завершено.

Следствие 1 . Высота призмы, описанной около цилиндра, равна высоте цилиндра.

Следствие 2. В любую прямую треугольную призму можно вписать цилиндр.

Справедливость этого утверждения вытекает из того факта, что в любой треугольник можно вписать окружность.

Следствие 3. В любую правильную n – угольную призму можно вписать цилиндр.

Для доказательства этого следствия достаточно заметить, правильная призма является прямой призмой. Основаниями правильной призмы являются правильные многоугольники, а в любой правильный n – угольник можно вписать окружность.

Видео:Призма, вписанная в цилиндр.The prism inscribed in the cylinder.Скачать

Отношение объемов цилиндра и описанной около него правильной n — угольной призмы

Задача. Найти отношение объемов цилиндра и описанной около него правильной n — угольной призмы.

Решение. Поскольку и объем цилиндра, и объем призмы объем призмы вычисляются по формуле

а высота цилиндра равна высоте описанной около него призмы, то для объемов цилиндра и описанной около него правильной n — угольной призмы справедливо равенство

Следствие 4. Отношение объема цилиндра к объему описанной около него правильной треугольной призмы правильной треугольной призмы равно

Следствие 5. Отношение объема цилиндра к объему описанной около него правильной четырехугольной призмы правильной четырехугольной призмы равно

Следствие 6. Отношение объема цилиндра к объему описанной около него правильной шестиугольной призмы равно

Видео:№ 4 - Геометрия 10-11 класс ПогореловСкачать

Тема урока «Призма, вписанная в цилиндр. Цилиндр, вписанный в призму»

Тип урока: ознакомление с новым материалом.

Технология урока: проблемно-исследовательская технология.

Рассмотреть понятия: вписанного цилиндра в призму и вписанной призмы в цилиндр;
Использовать эти понятия при решении задач;
Формировать представления об использовании этих понятий в практической жизни человека.

Метапредметные связи: геометрия, черчение, рабочие профессии.

Учащиеся должны знать:

Понятия: вписанного цилиндра в призму и вписанной призмы в цилиндр;
Применение данных понятий при решении задач;
Применение данных понятий в практической жизни.

Учащиеся должны уметь:

Решать задачи на взаимное расположение цилиндра и призмы;
Объяснять применение данных понятий в практической жизни человека.

Организационный момент (1 минута);
Постановка проблемы на определение темы урока и его целей. (3 минуты);
Актуализация знаний учащихся. Повторение ранее изученного материала (5 минут);
Объяснение новой темы. Проблемно-поисковая работа.(7 минут);
Закрепление изученных понятий в ходе фронтального опроса.(7 минут);
Решение задач различного уровня сложности. (15 минут);
Рефлексия. Итоговый тест по усвоению новых понятий с самопроверкой. (5 минут);
Подведение итогов урока. Домашнее задание.(1 минута).

Читайте также: Причина попадания масла в цилиндр мотоблока

1. Постановка проблемы: токарь из шестигранника вытачивает цилиндр.

Вопрос: о каком взаимном расположении геометрических тел идет речь? (слайд 1 из презентации к уроку)

Используя определенные инструменты, фрезеровщик из цилиндрической заготовки получает шестигранник.

Вопрос:о каком взаимном расположении геометрических тел идет речь? (слайд 2)

Тема урока “Цилиндр, вписанный в призму. Призма, вписанная в цилиндр”. (слайд 3)

Цели урока:

Рассмотреть понятия: вписанного цилиндра в призму и вписанной призмы в цилиндр;
Использовать эти понятия при решении задач;
Формировать представления об использовании этих понятий в практической жизни человека.(слайд 4)

2. Актуализация знаний учащихся. Повторение ранее изученного.

Повторение определений, связанных с понятиями “призма” и “цилиндр”:

В какой треугольник можно вписать окружность? Около какого треугольника можно описать окружность?
В какой четырехугольник можно вписать окружность? Около какого четырехугольника можно описать окружность?
Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной окружности. Памятка на столе (Приложение 1).
Решить задачу: Найдите боковое ребро правильной четырехугольной призмы, если сторона ее основания равна 9 см, а площадь поверхности равна 306 см 2 . У слабых учащихся лежит на столе решение этой задачи с пропусками, которые они должны заполнить во время работы (Приложение 2).
Жестянщик изготавливает 10 баков цилиндрической формы размерами 50 см в высоту и 40 см в диаметре. Сколько листов железа размерами 0,81,6 м потребуется для этого (5% листового железа идет на скрепление деталей)? Ответ округлите до целых. У слабых учащихся лежит на столе решение этой задачи с пропусками, которые они должны заполнить во время работы (Приложение 3).

3. Объяснение новой темы. Проблемно – поисковая работа.

Как вы думаете можно ли вписать в цилиндр призму?

При каких условиях призма вписана в цилиндр?

Призма прямая.
Основания призмы вписаны в основания цилиндра.
Боковые ребра призмы совпадают с образующими (слайд 6).

Как вы думаете можно ли описать около цилиндра призму?

При каких условиях около цилиндра можно описать призму?

Призма прямая.
Основания цилиндра вписаны в основания призмы.
Образующие цилиндра совпадают с боковыми ребрами призмы (слайд 7).

4. Закрепление изученных понятий в ходе фронтального опроса.

Можно ли описать цилиндр вокруг прямой призмы, в основании которой лежит ромб?
Можно ли вписать цилиндр в призму, в основании которой лежит прямоугольник?
Определите вид треугольника, лежащего в основании призмы, вписанной в цилиндр, если ось цилиндра проходит внутри призмы (слайд 8)?
В прямой четырехугольной призме углы основания в порядке следования относятся как 3:5:8:6. Можно ли описать цилиндр вокруг этой призмы?

Читайте также: Выжимной цилиндр тормоза ваз 2107

5. Решение задач различного уровня сложности по готовым чертежам.

В цилиндр вписана правильная шестиугольная призма, а вокруг него описана правильная четырехугольная призма.Найти отношение площадей боковых поверхностей этих призм (слайд 9).

Решение: = = = 3/4. Ответ: 3/4.

В основании прямой призмы лежит ромб. Площадь боковой поверхности призмы равна 120 см 2 . Найти радиус основания цилиндра, вписанного в эту призму, если высота призмы равна 6 см, а острый угол основания — 60°(слайд 10).

Решение S = Ph = , 120 = 4 * а * 6, а = 5см._осн = а 2 * , _осн = 25, _осн = (25):5 = , r = :2 = .

Прямоугольный параллелепипед со сторонами 6дм и 8дм и высотой, равной 14дм, вписан в цилиндр. Найдите радиус основания цилиндра, площадь полной поверхности цилиндра(слайд 11).

Ответ: r=5 дм, S=190 дм 2 .

Площадь осевого сечения цилиндра равна Q. Найти площадь боковой поверхности правильной шестиугольной призмы, описанной вокруг этого цилиндра (слайд 12).

6. Рефлексия. Итоговый тест по усвоению новых понятий с самопроверкой.

Верно ли утверждение: в наклонную призму можно вписать цилиндр?
Верно ли утверждение: высота цилиндра равна высоте, вписанной в него треугольной призме?
Верно ли утверждение: около любой треугольной призмы можно описать цилиндр?
Верно ли утверждение: в любую четырехугольную призму можно вписать цилиндр?
Верно ли утверждение: около правильной шестиугольной призмы можно описать цилиндр?
Верно ли утверждение: призму высотой 40 см можно вписать в цилиндр высотой 24 см?
Из тонкостенной цилиндрической трубы жестянщик делает четырехгранную водосточную трубу. Будут ли равны площади поверхностей этих труб?
Найдите боковое ребро правильной четырехугольной призмы, если сторона ее основания равна 2, а площадь поверхности равна 104.
Люди, каких профессий сталкиваются с понятиями: “вписанный цилиндр в призму” и “ вписанная призма в цилиндр”?

Выполнить самопроверку и проанализировать знания и умения, полученные на уроке (слайд13).

7. Итог урока. Домашнее задание.

1. Атанасян Л.Г., Бутузов В.Ф., Кадомцев С.Б. и др. Геометрия 10 – 11. Учебник для общеобразовательных учреждений. – 15-е изд.,доп. – М.: Просвещение, 2006.

2. Саакян С.М., Бутузов В.Ф. Изучение геометрии в 10 – 11 классах. Метод. рекомендации к учеб.: Кн. для учителя. – 2-изд. – М. Просвещение, 2003.